A Fourier Space Perspective on Diffusion Models

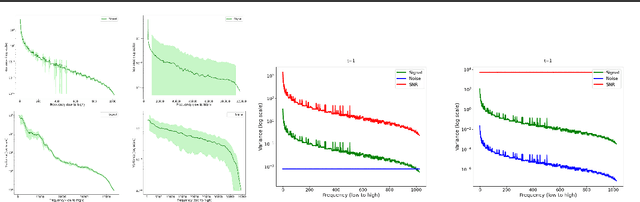
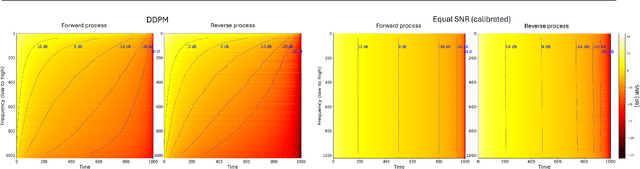
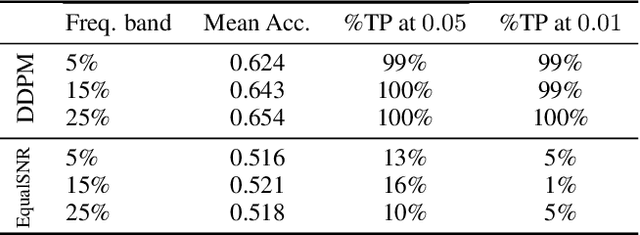
Diffusion models are state-of-the-art generative models on data modalities such as images, audio, proteins and materials. These modalities share the property of exponentially decaying variance and magnitude in the Fourier domain. Under the standard Denoising Diffusion Probabilistic Models (DDPM) forward process of additive white noise, this property results in high-frequency components being corrupted faster and earlier in terms of their Signal-to-Noise Ratio (SNR) than low-frequency ones. The reverse process then generates low-frequency information before high-frequency details. In this work, we study the inductive bias of the forward process of diffusion models in Fourier space. We theoretically analyse and empirically demonstrate that the faster noising of high-frequency components in DDPM results in violations of the normality assumption in the reverse process. Our experiments show that this leads to degraded generation quality of high-frequency components. We then study an alternate forward process in Fourier space which corrupts all frequencies at the same rate, removing the typical frequency hierarchy during generation, and demonstrate marked performance improvements on datasets where high frequencies are primary, while performing on par with DDPM on standard imaging benchmarks.

AIRIVA: A Deep Generative Model of Adaptive Immune Repertoires

Recent advances in immunomics have shown that T-cell receptor (TCR) signatures can accurately predict active or recent infection by leveraging the high specificity of TCR binding to disease antigens. However, the extreme diversity of the adaptive immune repertoire presents challenges in reliably identifying disease-specific TCRs. Population genetics and sequencing depth can also have strong systematic effects on repertoires, which requires careful consideration when developing diagnostic models. We present an Adaptive Immune Repertoire-Invariant Variational Autoencoder (AIRIVA), a generative model that learns a low-dimensional, interpretable, and compositional representation of TCR repertoires to disentangle such systematic effects in repertoires. We apply AIRIVA to two infectious disease case-studies: COVID-19 (natural infection and vaccination) and the Herpes Simplex Virus (HSV-1 and HSV-2), and empirically show that we can disentangle the individual disease signals. We further demonstrate AIRIVA's capability to: learn from unlabelled samples; generate in-silico TCR repertoires by intervening on the latent factors; and identify disease-associated TCRs validated using TCR annotations from external assay data.

Preferential Mixture-of-Experts: Interpretable Models that Rely on Human Expertise as much as Possible

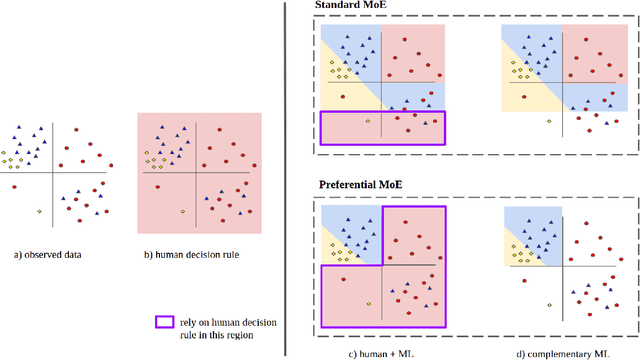
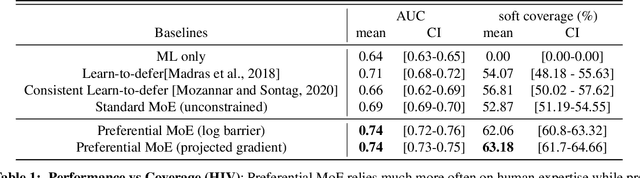
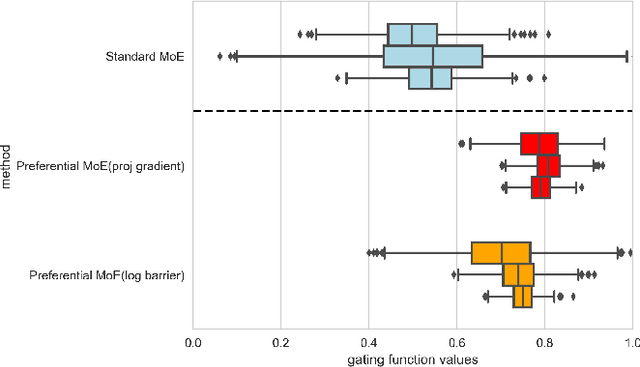
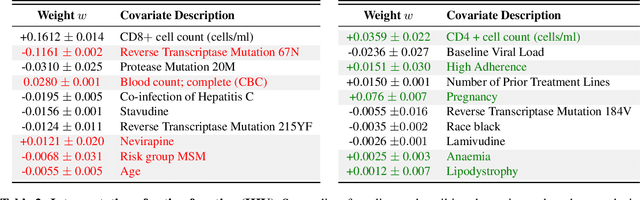
We propose Preferential MoE, a novel human-ML mixture-of-experts model that augments human expertise in decision making with a data-based classifier only when necessary for predictive performance. Our model exhibits an interpretable gating function that provides information on when human rules should be followed or avoided. The gating function is maximized for using human-based rules, and classification errors are minimized. We propose solving a coupled multi-objective problem with convex subproblems. We develop approximate algorithms and study their performance and convergence. Finally, we demonstrate the utility of Preferential MoE on two clinical applications for the treatment of Human Immunodeficiency Virus (HIV) and management of Major Depressive Disorder (MDD).

Convolutional Dictionary Learning in Hierarchical Networks

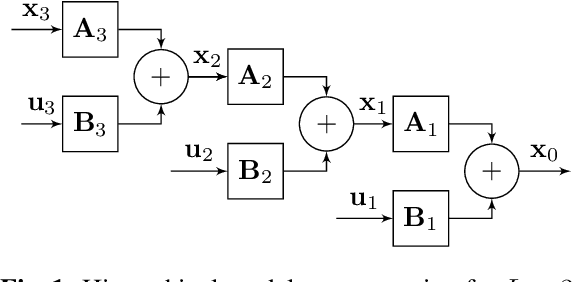
Filter banks are a popular tool for the analysis of piecewise smooth signals such as natural images. Motivated by the empirically observed properties of scale and detail coefficients of images in the wavelet domain, we propose a hierarchical deep generative model of piecewise smooth signals that is a recursion across scales: the low pass scale coefficients at one layer are obtained by filtering the scale coefficients at the next layer, and adding a high pass detail innovation obtained by filtering a sparse vector. This recursion describes a linear dynamic system that is a non-Gaussian Markov process across scales and is closely related to multilayer-convolutional sparse coding (ML-CSC) generative model for deep networks, except that our model allows for deeper architectures, and combines sparse and non-sparse signal representations. We propose an alternating minimization algorithm for learning the filters in this hierarchical model given observations at layer zero, e.g., natural images. The algorithm alternates between a coefficient-estimation step and a filter update step. The coefficient update step performs sparse (detail) and smooth (scale) coding and, when unfolded, leads to a deep neural network. We use MNIST to demonstrate the representation capabilities of the model, and its derived features (coefficients) for classification.

Learning Parametric Closed-Loop Policies for Markov Potential Games

Multiagent systems where agents interact among themselves and with a stochastic environment can be formalized as stochastic games. We study a subclass named Markov potential games (MPGs) that appear often in economic and engineering applications when the agents share a common resource. We consider MPGs with continuous state-action variables, coupled constraints and nonconvex rewards. Previous analysis followed a variational approach that is only valid for very simple cases (convex rewards, invertible dynamics, and no coupled constraints); or considered deterministic dynamics and provided open-loop (OL) analysis, studying strategies that consist in predefined action sequences, which are not optimal for stochastic environments. We present a closed-loop (CL) analysis for MPGs and consider parametric policies that depend on the current state. We provide easily verifiable, sufficient and necessary conditions for a stochastic game to be an MPG, even for complex parametric functions (e.g., deep neural networks); and show that a closed-loop Nash equilibrium (NE) can be found (or at least approximated) by solving a related optimal control problem (OCP). This is useful since solving an OCP--which is a single-objective problem--is usually much simpler than solving the original set of coupled OCPs that form the game--which is a multiobjective control problem. This is a considerable improvement over the previously standard approach for the CL analysis of MPGs, which gives no approximate solution if no NE belongs to the chosen parametric family, and which is practical only for simple parametric forms. We illustrate the theoretical contributions with an example by applying our approach to a noncooperative communications engineering game. We then solve the game with a deep reinforcement learning algorithm that learns policies that closely approximates an exact variational NE of the game.