Robust Multi-view Co-expression Network Inference

Unraveling the co-expression of genes across studies enhances the understanding of cellular processes. Inferring gene co-expression networks from transcriptome data presents many challenges, including spurious gene correlations, sample correlations, and batch effects. To address these complexities, we introduce a robust method for high-dimensional graph inference from multiple independent studies. We base our approach on the premise that each dataset is essentially a noisy linear mixture of gene loadings that follow a multivariate $t$-distribution with a sparse precision matrix, which is shared across studies. This allows us to show that we can identify the co-expression matrix up to a scaling factor among other model parameters. Our method employs an Expectation-Maximization procedure for parameter estimation. Empirical evaluation on synthetic and gene expression data demonstrates our method's improved ability to learn the underlying graph structure compared to baseline methods.

Deep anytime-valid hypothesis testing

We propose a general framework for constructing powerful, sequential hypothesis tests for a large class of nonparametric testing problems. The null hypothesis for these problems is defined in an abstract form using the action of two known operators on the data distribution. This abstraction allows for a unified treatment of several classical tasks, such as two-sample testing, independence testing, and conditional-independence testing, as well as modern problems, such as testing for adversarial robustness of machine learning (ML) models. Our proposed framework has the following advantages over classical batch tests: 1) it continuously monitors online data streams and efficiently aggregates evidence against the null, 2) it provides tight control over the type I error without the need for multiple testing correction, 3) it adapts the sample size requirement to the unknown hardness of the problem. We develop a principled approach of leveraging the representation capability of ML models within the testing-by-betting framework, a game-theoretic approach for designing sequential tests. Empirical results on synthetic and real-world datasets demonstrate that tests instantiated using our general framework are competitive against specialized baselines on several tasks.

E-Valuating Classifier Two-Sample Tests

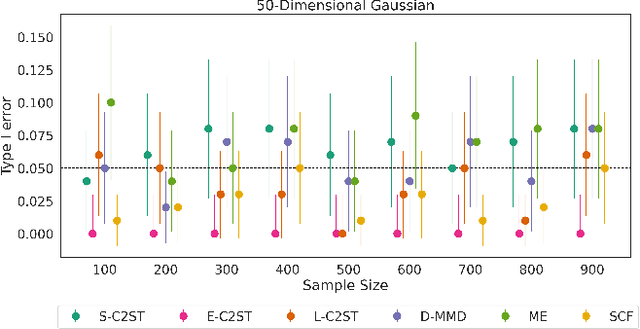
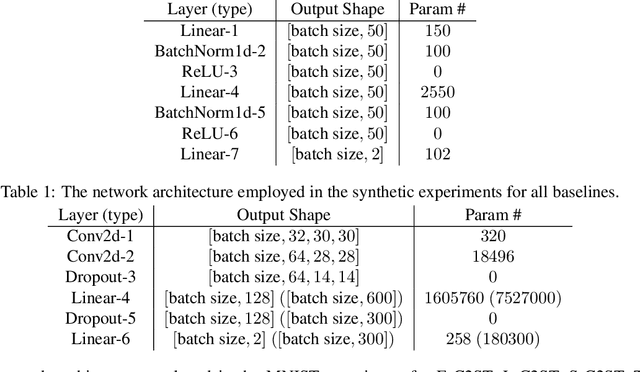
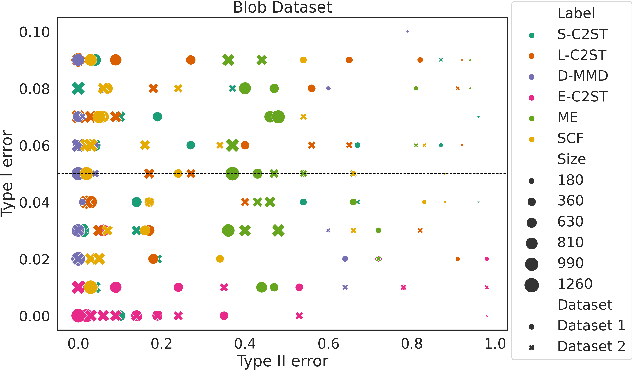
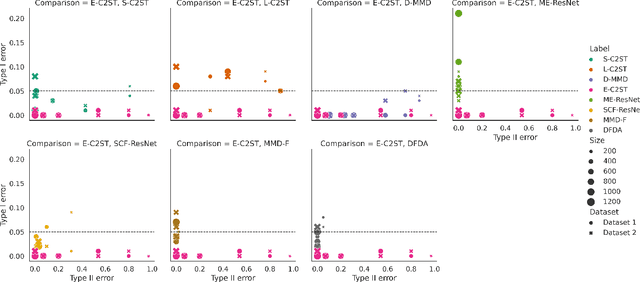
We propose E-C2ST, a classifier two-sample test for high-dimensional data based on E-values. Compared to $p$-values-based tests, tests with E-values have finite sample guarantees for the type I error. E-C2ST combines ideas from existing work on split likelihood ratio tests and predictive independence testing. The resulting E-values incorporate information about the alternative hypothesis. We demonstrate the utility of E-C2ST on simulated and real-life data. In all experiments, we observe that when going from small to large sample sizes, as expected, E-C2ST starts with lower power compared to other methods but eventually converges towards one. Simultaneously, E-C2ST's type I error stays substantially below the chosen significance level, which is not always the case for the baseline methods. Finally, we use an MRI dataset to demonstrate that multiplying E-values from multiple independently conducted studies leads to a combined E-value that retains the finite sample type I error guarantees while increasing the power.

Multi-View Independent Component Analysis with Shared and Individual Sources

Independent component analysis (ICA) is a blind source separation method for linear disentanglement of independent latent sources from observed data. We investigate the special setting of noisy linear ICA where the observations are split among different views, each receiving a mixture of shared and individual sources. We prove that the corresponding linear structure is identifiable, and the shared sources can be recovered, provided that sufficiently many diverse views and data points are available. To computationally estimate the sources, we optimize a constrained form of the joint log-likelihood of the observed data among all views. We show empirically that our objective recovers the sources in high dimensional settings, also in the case when the measurements are corrupted by noise. Finally, we apply the proposed model in a challenging real-life application, where the estimated shared sources from two large transcriptome datasets (observed data) provided by two different labs (two different views) lead to a more plausible representation of the underlying graph structure than existing baselines.

MMGAN: Generative Adversarial Networks for Multi-Modal Distributions

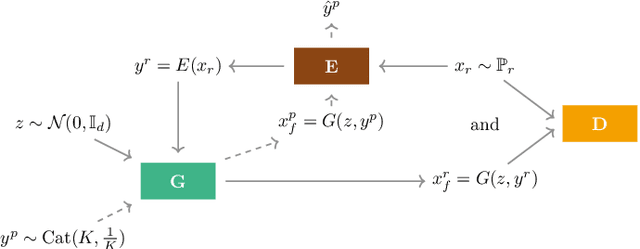
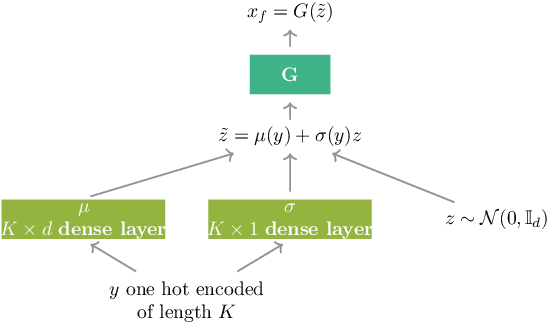
Over the past years, Generative Adversarial Networks (GANs) have shown a remarkable generation performance especially in image synthesis. Unfortunately, they are also known for having an unstable training process and might loose parts of the data distribution for heterogeneous input data. In this paper, we propose a novel GAN extension for multi-modal distribution learning (MMGAN). In our approach, we model the latent space as a Gaussian mixture model with a number of clusters referring to the number of disconnected data manifolds in the observation space, and include a clustering network, which relates each data manifold to one Gaussian cluster. Thus, the training gets more stable. Moreover, MMGAN allows for clustering real data according to the learned data manifold in the latent space. By a series of benchmark experiments, we illustrate that MMGAN outperforms competitive state-of-the-art models in terms of clustering performance.