A Fourier Space Perspective on Diffusion Models

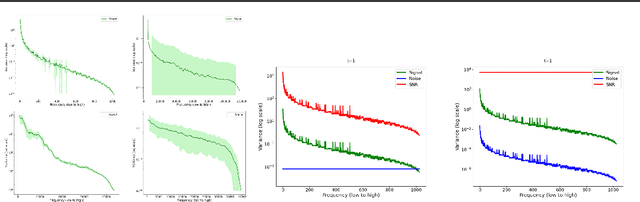
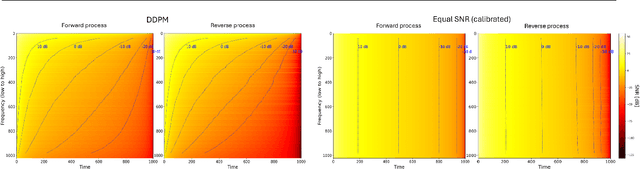
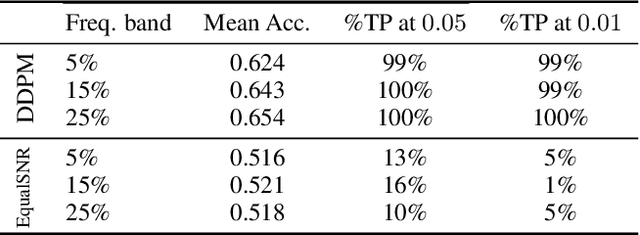
Diffusion models are state-of-the-art generative models on data modalities such as images, audio, proteins and materials. These modalities share the property of exponentially decaying variance and magnitude in the Fourier domain. Under the standard Denoising Diffusion Probabilistic Models (DDPM) forward process of additive white noise, this property results in high-frequency components being corrupted faster and earlier in terms of their Signal-to-Noise Ratio (SNR) than low-frequency ones. The reverse process then generates low-frequency information before high-frequency details. In this work, we study the inductive bias of the forward process of diffusion models in Fourier space. We theoretically analyse and empirically demonstrate that the faster noising of high-frequency components in DDPM results in violations of the normality assumption in the reverse process. Our experiments show that this leads to degraded generation quality of high-frequency components. We then study an alternate forward process in Fourier space which corrupts all frequencies at the same rate, removing the typical frequency hierarchy during generation, and demonstrate marked performance improvements on datasets where high frequencies are primary, while performing on par with DDPM on standard imaging benchmarks.

On Learning Parallel Pancakes with Mostly Uniform Weights

We study the complexity of learning $k$-mixtures of Gaussians ($k$-GMMs) on $\mathbb{R}^d$. This task is known to have complexity $d^{\Omega(k)}$ in full generality. To circumvent this exponential lower bound on the number of components, research has focused on learning families of GMMs satisfying additional structural properties. A natural assumption posits that the component weights are not exponentially small and that the components have the same unknown covariance. Recent work gave a $d^{O(\log(1/w_{\min}))}$-time algorithm for this class of GMMs, where $w_{\min}$ is the minimum weight. Our first main result is a Statistical Query (SQ) lower bound showing that this quasi-polynomial upper bound is essentially best possible, even for the special case of uniform weights. Specifically, we show that it is SQ-hard to distinguish between such a mixture and the standard Gaussian. We further explore how the distribution of weights affects the complexity of this task. Our second main result is a quasi-polynomial upper bound for the aforementioned testing task when most of the weights are uniform while a small fraction of the weights are potentially arbitrary.

Batch List-Decodable Linear Regression via Higher Moments

We study the task of list-decodable linear regression using batches. A batch is called clean if it consists of i.i.d. samples from an unknown linear regression distribution. For a parameter $\alpha \in (0, 1/2)$, an unknown $\alpha$-fraction of the batches are clean and no assumptions are made on the remaining ones. The goal is to output a small list of vectors at least one of which is close to the true regressor vector in $\ell_2$-norm. [DJKS23] gave an efficient algorithm, under natural distributional assumptions, with the following guarantee. Assuming that the batch size $n$ satisfies $n \geq \tilde{\Omega}(\alpha^{-1})$ and the number of batches is $m = \mathrm{poly}(d, n, 1/\alpha)$, their algorithm runs in polynomial time and outputs a list of $O(1/\alpha^2)$ vectors at least one of which is $\tilde{O}(\alpha^{-1/2}/\sqrt{n})$ close to the target regressor. Here we design a new polynomial time algorithm with significantly stronger guarantees under the assumption that the low-degree moments of the covariates distribution are Sum-of-Squares (SoS) certifiably bounded. Specifically, for any constant $\delta>0$, as long as the batch size is $n \geq \Omega_{\delta}(\alpha^{-\delta})$ and the degree-$\Theta(1/\delta)$ moments of the covariates are SoS certifiably bounded, our algorithm uses $m = \mathrm{poly}((dn)^{1/\delta}, 1/\alpha)$ batches, runs in polynomial-time, and outputs an $O(1/\alpha)$-sized list of vectors one of which is $O(\alpha^{-\delta/2}/\sqrt{n})$ close to the target. That is, our algorithm achieves substantially smaller minimum batch size and final error, while achieving the optimal list size. Our approach uses higher-order moment information by carefully combining the SoS paradigm interleaved with an iterative method and a novel list pruning procedure. In the process, we give an SoS proof of the Marcinkiewicz-Zygmund inequality that may be of broader applicability.

Learning a Single Neuron Robustly to Distributional Shifts and Adversarial Label Noise

We study the problem of learning a single neuron with respect to the $L_2^2$-loss in the presence of adversarial distribution shifts, where the labels can be arbitrary, and the goal is to find a ``best-fit'' function. More precisely, given training samples from a reference distribution $\mathcal{p}_0$, the goal is to approximate the vector $\mathbf{w}^*$ which minimizes the squared loss with respect to the worst-case distribution that is close in $\chi^2$-divergence to $\mathcal{p}_{0}$. We design a computationally efficient algorithm that recovers a vector $ \hat{\mathbf{w}}$ satisfying $\mathbb{E}_{\mathcal{p}^*} (\sigma(\hat{\mathbf{w}} \cdot \mathbf{x}) - y)^2 \leq C \, \mathbb{E}_{\mathcal{p}^*} (\sigma(\mathbf{w}^* \cdot \mathbf{x}) - y)^2 + \epsilon$, where $C>1$ is a dimension-independent constant and $(\mathbf{w}^*, \mathcal{p}^*)$ is the witness attaining the min-max risk $\min_{\mathbf{w}~:~\|\mathbf{w}\| \leq W} \max_{\mathcal{p}} \mathbb{E}_{(\mathbf{x}, y) \sim \mathcal{p}} (\sigma(\mathbf{w} \cdot \mathbf{x}) - y)^2 - \nu \chi^2(\mathcal{p}, \mathcal{p}_0)$. Our algorithm follows a primal-dual framework and is designed by directly bounding the risk with respect to the original, nonconvex $L_2^2$ loss. From an optimization standpoint, our work opens new avenues for the design of primal-dual algorithms under structured nonconvexity.

Sum-of-squares lower bounds for Non-Gaussian Component Analysis

Non-Gaussian Component Analysis (NGCA) is the statistical task of finding a non-Gaussian direction in a high-dimensional dataset. Specifically, given i.i.d.\ samples from a distribution $P^A_{v}$ on $\mathbb{R}^n$ that behaves like a known distribution $A$ in a hidden direction $v$ and like a standard Gaussian in the orthogonal complement, the goal is to approximate the hidden direction. The standard formulation posits that the first $k-1$ moments of $A$ match those of the standard Gaussian and the $k$-th moment differs. Under mild assumptions, this problem has sample complexity $O(n)$. On the other hand, all known efficient algorithms require $\Omega(n^{k/2})$ samples. Prior work developed sharp Statistical Query and low-degree testing lower bounds suggesting an information-computation tradeoff for this problem. Here we study the complexity of NGCA in the Sum-of-Squares (SoS) framework. Our main contribution is the first super-constant degree SoS lower bound for NGCA. Specifically, we show that if the non-Gaussian distribution $A$ matches the first $(k-1)$ moments of $\mathcal{N}(0, 1)$ and satisfies other mild conditions, then with fewer than $n^{(1 - \varepsilon)k/2}$ many samples from the normal distribution, with high probability, degree $(\log n)^{{1\over 2}-o_n(1)}$ SoS fails to refute the existence of such a direction $v$. Our result significantly strengthens prior work by establishing a super-polynomial information-computation tradeoff against a broader family of algorithms. As corollaries, we obtain SoS lower bounds for several problems in robust statistics and the learning of mixture models. Our SoS lower bound proof introduces a novel technique, that we believe may be of broader interest, and a number of refinements over existing methods.

Robust Sparse Estimation for Gaussians with Optimal Error under Huber Contamination

We study Gaussian sparse estimation tasks in Huber's contamination model with a focus on mean estimation, PCA, and linear regression. For each of these tasks, we give the first sample and computationally efficient robust estimators with optimal error guarantees, within constant factors. All prior efficient algorithms for these tasks incur quantitatively suboptimal error. Concretely, for Gaussian robust $k$-sparse mean estimation on $\mathbb{R}^d$ with corruption rate $\epsilon>0$, our algorithm has sample complexity $(k^2/\epsilon^2)\mathrm{polylog}(d/\epsilon)$, runs in sample polynomial time, and approximates the target mean within $\ell_2$-error $O(\epsilon)$. Previous efficient algorithms inherently incur error $\Omega(\epsilon \sqrt{\log(1/\epsilon)})$. At the technical level, we develop a novel multidimensional filtering method in the sparse regime that may find other applications.

Multi-Model 3D Registration: Finding Multiple Moving Objects in Cluttered Point Clouds

We investigate a variation of the 3D registration problem, named multi-model 3D registration. In the multi-model registration problem, we are given two point clouds picturing a set of objects at different poses (and possibly including points belonging to the background) and we want to simultaneously reconstruct how all objects moved between the two point clouds. This setup generalizes standard 3D registration where one wants to reconstruct a single pose, e.g., the motion of the sensor picturing a static scene. Moreover, it provides a mathematically grounded formulation for relevant robotics applications, e.g., where a depth sensor onboard a robot perceives a dynamic scene and has the goal of estimating its own motion (from the static portion of the scene) while simultaneously recovering the motion of all dynamic objects. We assume a correspondence-based setup where we have putative matches between the two point clouds and consider the practical case where these correspondences are plagued with outliers. We then propose a simple approach based on Expectation-Maximization (EM) and establish theoretical conditions under which the EM approach converges to the ground truth. We evaluate the approach in simulated and real datasets ranging from table-top scenes to self-driving scenarios and demonstrate its effectiveness when combined with state-of-the-art scene flow methods to establish dense correspondences.

Distribution-Independent Regression for Generalized Linear Models with Oblivious Corruptions

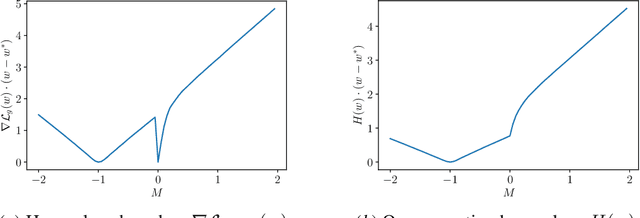
We demonstrate the first algorithms for the problem of regression for generalized linear models (GLMs) in the presence of additive oblivious noise. We assume we have sample access to examples $(x, y)$ where $y$ is a noisy measurement of $g(w^* \cdot x)$. In particular, \new{the noisy labels are of the form} $y = g(w^* \cdot x) + \xi + \epsilon$, where $\xi$ is the oblivious noise drawn independently of $x$ \new{and satisfies} $\Pr[\xi = 0] \geq o(1)$, and $\epsilon \sim \mathcal N(0, \sigma^2)$. Our goal is to accurately recover a \new{parameter vector $w$ such that the} function $g(w \cdot x)$ \new{has} arbitrarily small error when compared to the true values $g(w^* \cdot x)$, rather than the noisy measurements $y$. We present an algorithm that tackles \new{this} problem in its most general distribution-independent setting, where the solution may not \new{even} be identifiable. \new{Our} algorithm returns \new{an accurate estimate of} the solution if it is identifiable, and otherwise returns a small list of candidates, one of which is close to the true solution. Furthermore, we \new{provide} a necessary and sufficient condition for identifiability, which holds in broad settings. \new{Specifically,} the problem is identifiable when the quantile at which $\xi + \epsilon = 0$ is known, or when the family of hypotheses does not contain candidates that are nearly equal to a translated $g(w^* \cdot x) + A$ for some real number $A$, while also having large error when compared to $g(w^* \cdot x)$. This is the first \new{algorithmic} result for GLM regression \new{with oblivious noise} which can handle more than half the samples being arbitrarily corrupted. Prior work focused largely on the setting of linear regression, and gave algorithms under restrictive assumptions.

List-Decodable Sparse Mean Estimation via Difference-of-Pairs Filtering

We study the problem of list-decodable sparse mean estimation. Specifically, for a parameter $\alpha \in (0, 1/2)$, we are given $m$ points in $\mathbb{R}^n$, $\lfloor \alpha m \rfloor$ of which are i.i.d. samples from a distribution $D$ with unknown $k$-sparse mean $\mu$. No assumptions are made on the remaining points, which form the majority of the dataset. The goal is to return a small list of candidates containing a vector $\widehat \mu$ such that $\| \widehat \mu - \mu \|_2$ is small. Prior work had studied the problem of list-decodable mean estimation in the dense setting. In this work, we develop a novel, conceptually simpler technique for list-decodable mean estimation. As the main application of our approach, we provide the first sample and computationally efficient algorithm for list-decodable sparse mean estimation. In particular, for distributions with ``certifiably bounded'' $t$-th moments in $k$-sparse directions and sufficiently light tails, our algorithm achieves error of $(1/\alpha)^{O(1/t)}$ with sample complexity $m = (k\log(n))^{O(t)}/\alpha$ and running time $\mathrm{poly}(mn^t)$. For the special case of Gaussian inliers, our algorithm achieves the optimal error guarantee of $\Theta (\sqrt{\log(1/\alpha)})$ with quasi-polynomial sample and computational complexity. We complement our upper bounds with nearly-matching statistical query and low-degree polynomial testing lower bounds.

Robust Sparse Mean Estimation via Sum of Squares

We study the problem of high-dimensional sparse mean estimation in the presence of an $\epsilon$-fraction of adversarial outliers. Prior work obtained sample and computationally efficient algorithms for this task for identity-covariance subgaussian distributions. In this work, we develop the first efficient algorithms for robust sparse mean estimation without a priori knowledge of the covariance. For distributions on $\mathbb R^d$ with "certifiably bounded" $t$-th moments and sufficiently light tails, our algorithm achieves error of $O(\epsilon^{1-1/t})$ with sample complexity $m = (k\log(d))^{O(t)}/\epsilon^{2-2/t}$. For the special case of the Gaussian distribution, our algorithm achieves near-optimal error of $\tilde O(\epsilon)$ with sample complexity $m = O(k^4 \mathrm{polylog}(d))/\epsilon^2$. Our algorithms follow the Sum-of-Squares based, proofs to algorithms approach. We complement our upper bounds with Statistical Query and low-degree polynomial testing lower bounds, providing evidence that the sample-time-error tradeoffs achieved by our algorithms are qualitatively the best possible.