Edward Meeds
A Fourier Space Perspective on Diffusion Models
May 16, 2025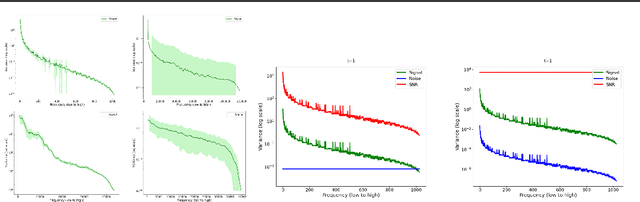

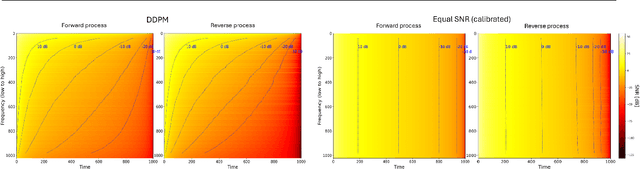
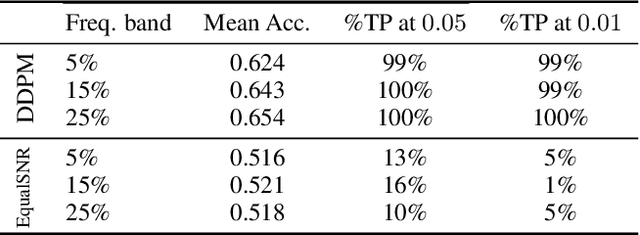
Abstract:Diffusion models are state-of-the-art generative models on data modalities such as images, audio, proteins and materials. These modalities share the property of exponentially decaying variance and magnitude in the Fourier domain. Under the standard Denoising Diffusion Probabilistic Models (DDPM) forward process of additive white noise, this property results in high-frequency components being corrupted faster and earlier in terms of their Signal-to-Noise Ratio (SNR) than low-frequency ones. The reverse process then generates low-frequency information before high-frequency details. In this work, we study the inductive bias of the forward process of diffusion models in Fourier space. We theoretically analyse and empirically demonstrate that the faster noising of high-frequency components in DDPM results in violations of the normality assumption in the reverse process. Our experiments show that this leads to degraded generation quality of high-frequency components. We then study an alternate forward process in Fourier space which corrupts all frequencies at the same rate, removing the typical frequency hierarchy during generation, and demonstrate marked performance improvements on datasets where high frequencies are primary, while performing on par with DDPM on standard imaging benchmarks.
Towards Efficient Optimizer Design for LLM via Structured Fisher Approximation with a Low-Rank Extension
Feb 11, 2025
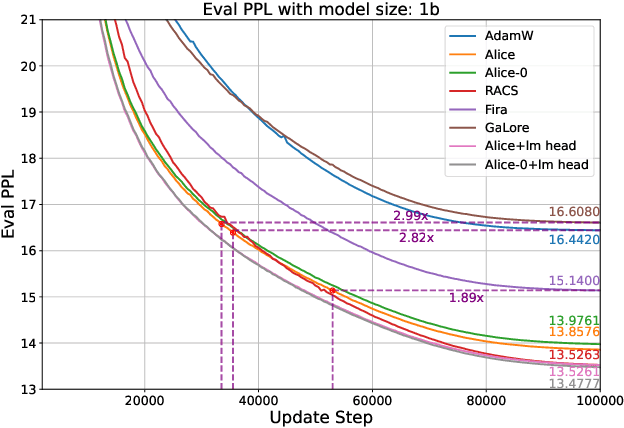
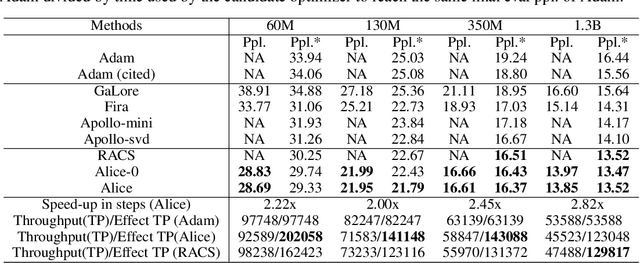
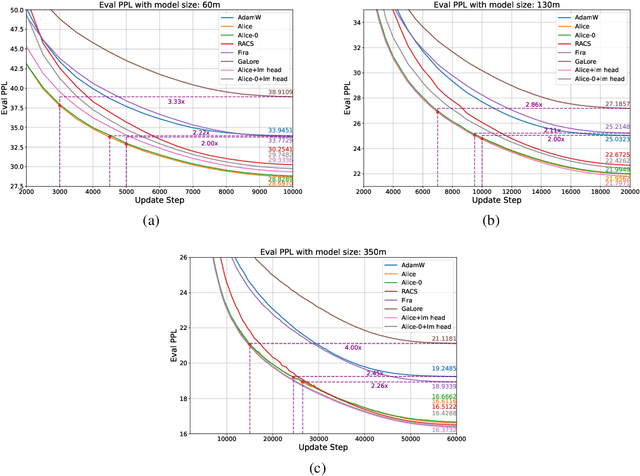
Abstract:Designing efficient optimizers for large language models (LLMs) with low-memory requirements and fast convergence is an important and challenging problem. This paper makes a step towards the systematic design of such optimizers through the lens of structured Fisher information matrix (FIM) approximation. We show that many state-of-the-art efficient optimizers can be viewed as solutions to FIM approximation (under the Frobenius norm) with specific structural assumptions. Building on these insights, we propose two design recommendations of practical efficient optimizers for LLMs, involving the careful selection of structural assumptions to balance generality and efficiency, and enhancing memory efficiency of optimizers with general structures through a novel low-rank extension framework. We demonstrate how to use each design approach by deriving new memory-efficient optimizers: Row and Column Scaled SGD (RACS) and Adaptive low-dimensional subspace estimation (Alice). Experiments on LLaMA pre-training (up to 1B parameters) validate the effectiveness, showing faster and better convergence than existing memory-efficient baselines and Adam with little memory overhead. Notably, Alice achieves better than 2x faster convergence over Adam, while RACS delivers strong performance on the 1B model with SGD-like memory.
Gradient Multi-Normalization for Stateless and Scalable LLM Training
Feb 10, 2025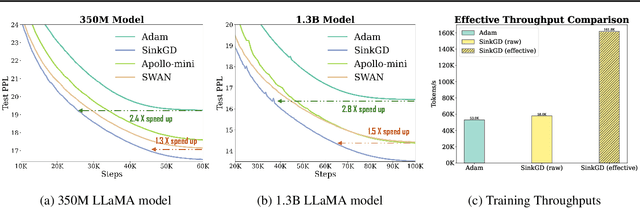
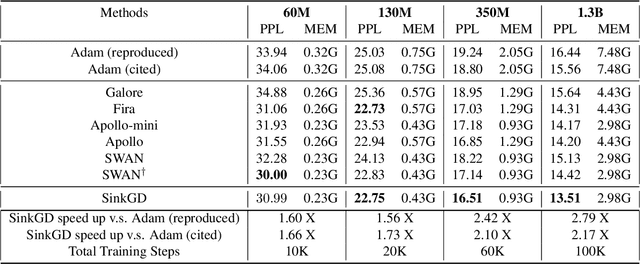
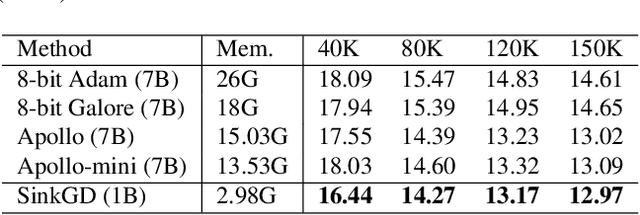

Abstract:Training large language models (LLMs) typically relies on adaptive optimizers like Adam (Kingma & Ba, 2015) which store additional state information to accelerate convergence but incur significant memory overhead. Recent efforts, such as SWAN (Ma et al., 2024) address this by eliminating the need for optimizer states while achieving performance comparable to Adam via a multi-step preprocessing procedure applied to instantaneous gradients. Motivated by the success of SWAN, we introduce a novel framework for designing stateless optimizers that normalizes stochastic gradients according to multiple norms. To achieve this, we propose a simple alternating scheme to enforce the normalization of gradients w.r.t these norms. We show that our procedure can produce, up to an arbitrary precision, a fixed-point of the problem, and that SWAN is a particular instance of our approach with carefully chosen norms, providing a deeper understanding of its design. However, SWAN's computationally expensive whitening/orthogonalization step limit its practicality for large LMs. Using our principled perspective, we develop of a more efficient, scalable, and practical stateless optimizer. Our algorithm relaxes the properties of SWAN, significantly reducing its computational cost while retaining its memory efficiency, making it applicable to training large-scale models. Experiments on pre-training LLaMA models with up to 1 billion parameters demonstrate a 3X speedup over Adam with significantly reduced memory requirements, outperforming other memory-efficient baselines.
SWAN: SGD with Normalization and Whitening Enables Stateless LLM Training
Dec 23, 2024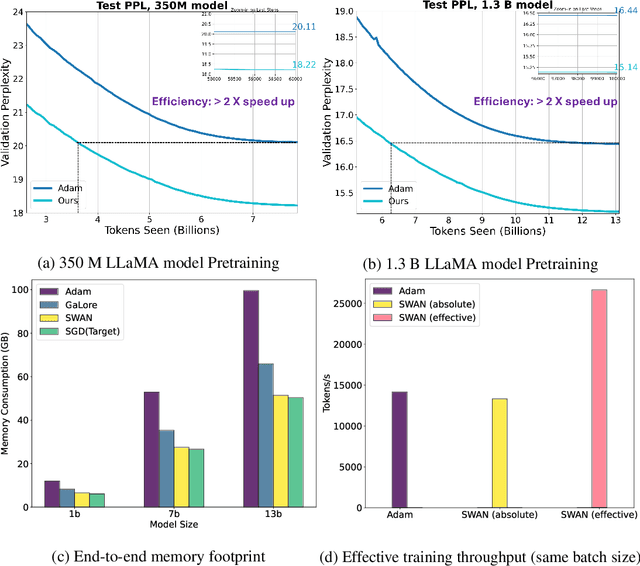



Abstract:Adaptive optimizers such as Adam (Kingma & Ba, 2015) have been central to the success of large language models. However, they often require to maintain optimizer states throughout training, which can result in memory requirements several times greater than the model footprint. This overhead imposes constraints on scalability and computational efficiency. Stochastic Gradient Descent (SGD), in contrast, is a stateless optimizer, as it does not track state variables during training. Consequently, it achieves optimal memory efficiency. However, its capability in LLM training is limited (Zhao et al., 2024b). In this work, we show that pre-processing SGD in a stateless manner can achieve the same performance as the Adam optimizer for LLM training, while drastically reducing the memory cost. Specifically, we propose to pre-process the instantaneous stochastic gradients using normalization and whitening. We show that normalization stabilizes gradient distributions, and whitening counteracts the local curvature of the loss landscape. This results in SWAN (SGD with Whitening And Normalization), a stochastic optimizer that eliminates the need to store any optimizer states. Empirically, SWAN has the same memory footprint as SGD, achieving $\approx 50\%$ reduction on total end-to-end memory compared to Adam. In language modeling tasks, SWAN demonstrates comparable or even better performance than Adam: when pre-training the LLaMA model with 350M and 1.3B parameters, SWAN achieves a 2x speedup by reaching the same evaluation perplexity using half as many tokens.
SWAN: Preprocessing SGD Enables Adam-Level Performance On LLM Training With Significant Memory Reduction
Dec 17, 2024



Abstract:Adaptive optimizers such as Adam (Kingma & Ba, 2015) have been central to the success of large language models. However, they maintain additional moving average states throughout training, which results in memory requirements several times greater than the model. This overhead imposes constraints on scalability and computational efficiency. On the other hand, while stochastic gradient descent (SGD) is optimal in terms of memory efficiency, their capability in LLM training is limited (Zhao et al., 2024b). To address this dilemma, we show that pre-processing SGD is sufficient to reach Adam-level performance on LLMs. Specifically, we propose to preprocess the instantaneous stochastic gradients with two simple operators: $\mathtt{GradNorm}$ and $\mathtt{GradWhitening}$. $\mathtt{GradNorm}$ stabilizes gradient distributions, and $\mathtt{GradWhitening}$ counteracts the local curvature of the loss landscape, respectively. This results in SWAN (SGD with Whitening And Normalization), a stochastic optimizer that eliminates the need to store any accumulative state variables. Empirically, SWAN has the same memory footprint as SGD, achieving $\approx 50\%$ reduction on total end-to-end memory compared to Adam. In language modeling tasks, SWAN demonstrates the same or even a substantial improvement over Adam. Specifically, when pre-training the LLaMa model with 350M and 1.3B parameters, SWAN achieves a 2x speedup by reaching the same evaluation perplexity in less than half tokens seen.
AIRIVA: A Deep Generative Model of Adaptive Immune Repertoires
Apr 26, 2023



Abstract:Recent advances in immunomics have shown that T-cell receptor (TCR) signatures can accurately predict active or recent infection by leveraging the high specificity of TCR binding to disease antigens. However, the extreme diversity of the adaptive immune repertoire presents challenges in reliably identifying disease-specific TCRs. Population genetics and sequencing depth can also have strong systematic effects on repertoires, which requires careful consideration when developing diagnostic models. We present an Adaptive Immune Repertoire-Invariant Variational Autoencoder (AIRIVA), a generative model that learns a low-dimensional, interpretable, and compositional representation of TCR repertoires to disentangle such systematic effects in repertoires. We apply AIRIVA to two infectious disease case-studies: COVID-19 (natural infection and vaccination) and the Herpes Simplex Virus (HSV-1 and HSV-2), and empirically show that we can disentangle the individual disease signals. We further demonstrate AIRIVA's capability to: learn from unlabelled samples; generate in-silico TCR repertoires by intervening on the latent factors; and identify disease-associated TCRs validated using TCR annotations from external assay data.
Capturing Actionable Dynamics with Structured Latent Ordinary Differential Equations
Feb 25, 2022



Abstract:End-to-end learning of dynamical systems with black-box models, such as neural ordinary differential equations (ODEs), provides a flexible framework for learning dynamics from data without prescribing a mathematical model for the dynamics. Unfortunately, this flexibility comes at the cost of understanding the dynamical system, for which ODEs are used ubiquitously. Further, experimental data are collected under various conditions (inputs), such as treatments, or grouped in some way, such as part of sub-populations. Understanding the effects of these system inputs on system outputs is crucial to have any meaningful model of a dynamical system. To that end, we propose a structured latent ODE model that explicitly captures system input variations within its latent representation. Building on a static latent variable specification, our model learns (independent) stochastic factors of variation for each input to the system, thus separating the effects of the system inputs in the latent space. This approach provides actionable modeling through the controlled generation of time-series data for novel input combinations (or perturbations). Additionally, we propose a flexible approach for quantifying uncertainties, leveraging a quantile regression formulation. Experimental results on challenging biological datasets show consistent improvements over competitive baselines in the controlled generation of observational data and prediction of biologically meaningful system inputs.
Efficient Amortised Bayesian Inference for Hierarchical and Nonlinear Dynamical Systems
May 28, 2019

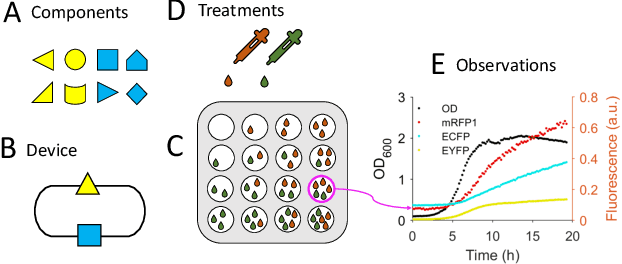
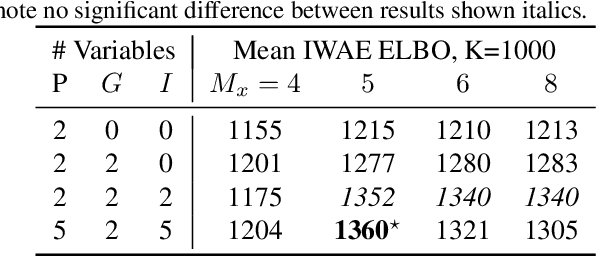
Abstract:We introduce a flexible, scalable Bayesian inference framework for nonlinear dynamical systems characterised by distinct and hierarchical variability at the individual, group, and population levels. Our model class is a generalisation of nonlinear mixed-effects (NLME) dynamical systems, the statistical workhorse for many experimental sciences. We cast parameter inference as stochastic optimisation of an end-to-end differentiable, block-conditional variational autoencoder. We specify the dynamics of the data-generating process as an ordinary differential equation (ODE) such that both the ODE and its solver are fully differentiable. This model class is highly flexible: the ODE right-hand sides can be a mixture of user-prescribed or "white-box" sub-components and neural network or "black-box" sub-components. Using stochastic optimisation, our amortised inference algorithm could seamlessly scale up to massive data collection pipelines (common in labs with robotic automation). Finally, our framework supports interpretability with respect to the underlying dynamics, as well as predictive generalization to unseen combinations of group components (also called "zero-shot" learning). We empirically validate our method by predicting the dynamic behaviour of bacteria that were genetically engineered to function as biosensors.
Fixing Variational Bayes: Deterministic Variational Inference for Bayesian Neural Networks
Oct 09, 2018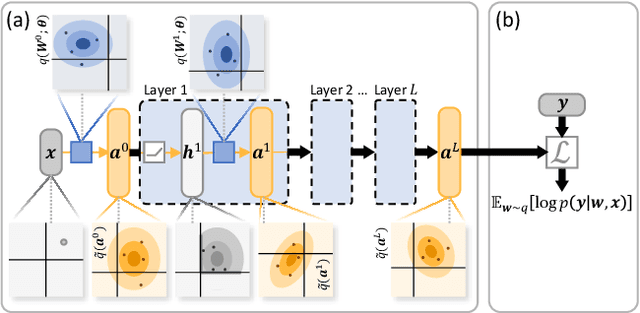
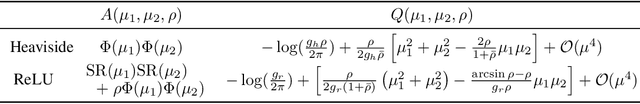
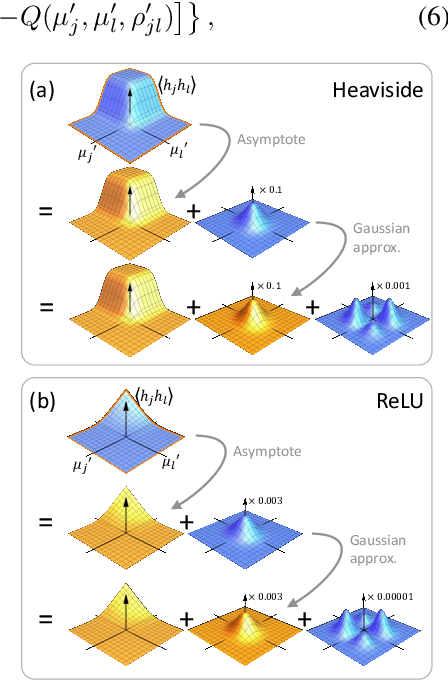
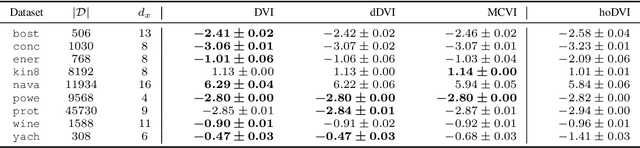
Abstract:Bayesian neural networks (BNNs) hold great promise as a flexible and principled solution to deal with uncertainty when learning from finite data. Among approaches to realize probabilistic inference in deep neural networks, variational Bayes (VB) is theoretically grounded, generally applicable, and computationally efficient. With wide recognition of potential advantages, why is it that variational Bayes has seen very limited practical use for BNNs in real applications? We argue that variational inference in neural networks is fragile: successful implementations require careful initialization and tuning of prior variances, as well as controlling the variance of Monte Carlo gradient estimates. We fix VB and turn it into a robust inference tool for Bayesian neural networks. We achieve this with two innovations: first, we introduce a novel deterministic method to approximate moments in neural networks, eliminating gradient variance; second, we introduce a hierarchical prior for parameters and a novel empirical Bayes procedure for automatically selecting prior variances. Combining these two innovations, the resulting method is highly efficient and robust. On the application of heteroscedastic regression we demonstrate strong predictive performance over alternative approaches.
Soft Weight-Sharing for Neural Network Compression
May 09, 2017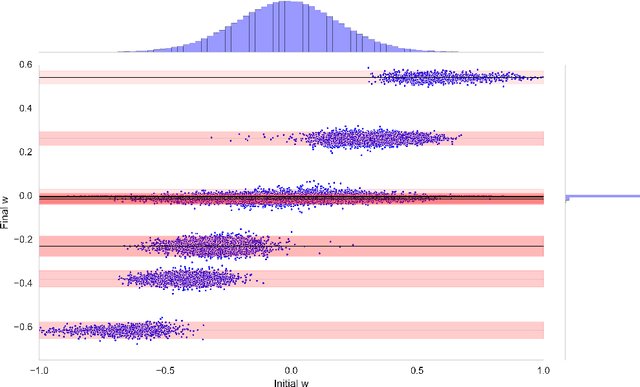
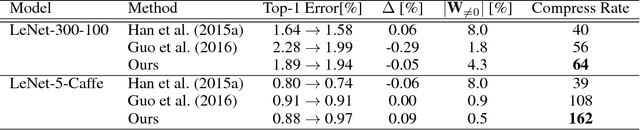
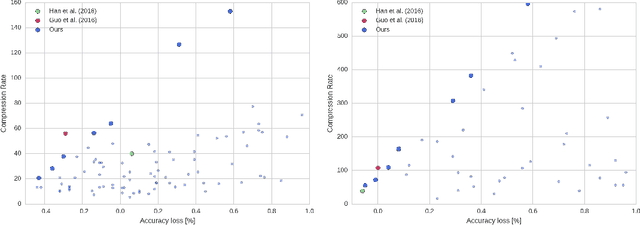
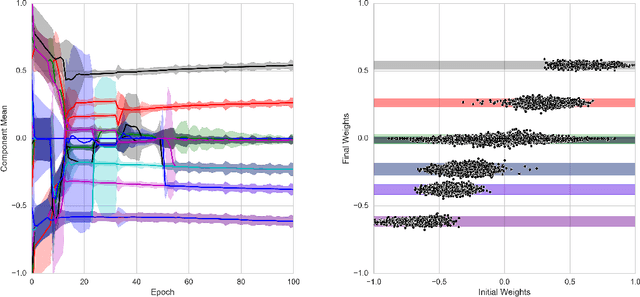
Abstract:The success of deep learning in numerous application domains created the de- sire to run and train them on mobile devices. This however, conflicts with their computationally, memory and energy intense nature, leading to a growing interest in compression. Recent work by Han et al. (2015a) propose a pipeline that involves retraining, pruning and quantization of neural network weights, obtaining state-of-the-art compression rates. In this paper, we show that competitive compression rates can be achieved by using a version of soft weight-sharing (Nowlan & Hinton, 1992). Our method achieves both quantization and pruning in one simple (re-)training procedure. This point of view also exposes the relation between compression and the minimum description length (MDL) principle.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge