AIRIVA: A Deep Generative Model of Adaptive Immune Repertoires

Recent advances in immunomics have shown that T-cell receptor (TCR) signatures can accurately predict active or recent infection by leveraging the high specificity of TCR binding to disease antigens. However, the extreme diversity of the adaptive immune repertoire presents challenges in reliably identifying disease-specific TCRs. Population genetics and sequencing depth can also have strong systematic effects on repertoires, which requires careful consideration when developing diagnostic models. We present an Adaptive Immune Repertoire-Invariant Variational Autoencoder (AIRIVA), a generative model that learns a low-dimensional, interpretable, and compositional representation of TCR repertoires to disentangle such systematic effects in repertoires. We apply AIRIVA to two infectious disease case-studies: COVID-19 (natural infection and vaccination) and the Herpes Simplex Virus (HSV-1 and HSV-2), and empirically show that we can disentangle the individual disease signals. We further demonstrate AIRIVA's capability to: learn from unlabelled samples; generate in-silico TCR repertoires by intervening on the latent factors; and identify disease-associated TCRs validated using TCR annotations from external assay data.

Capturing Actionable Dynamics with Structured Latent Ordinary Differential Equations

End-to-end learning of dynamical systems with black-box models, such as neural ordinary differential equations (ODEs), provides a flexible framework for learning dynamics from data without prescribing a mathematical model for the dynamics. Unfortunately, this flexibility comes at the cost of understanding the dynamical system, for which ODEs are used ubiquitously. Further, experimental data are collected under various conditions (inputs), such as treatments, or grouped in some way, such as part of sub-populations. Understanding the effects of these system inputs on system outputs is crucial to have any meaningful model of a dynamical system. To that end, we propose a structured latent ODE model that explicitly captures system input variations within its latent representation. Building on a static latent variable specification, our model learns (independent) stochastic factors of variation for each input to the system, thus separating the effects of the system inputs in the latent space. This approach provides actionable modeling through the controlled generation of time-series data for novel input combinations (or perturbations). Additionally, we propose a flexible approach for quantifying uncertainties, leveraging a quantile regression formulation. Experimental results on challenging biological datasets show consistent improvements over competitive baselines in the controlled generation of observational data and prediction of biologically meaningful system inputs.

Flexible Triggering Kernels for Hawkes Process Modeling

Recently proposed encoder-decoder structures for modeling Hawkes processes use transformer-inspired architectures, which encode the history of events via embeddings and self-attention mechanisms. These models deliver better prediction and goodness-of-fit than their RNN-based counterparts. However, they often require high computational and memory complexity requirements and sometimes fail to adequately capture the triggering function of the underlying process. So motivated, we introduce an efficient and general encoding of the historical event sequence by replacing the complex (multilayered) attention structures with triggering kernels of the observed data. Noting the similarity between the triggering kernels of a point process and the attention scores, we use a triggering kernel to replace the weights used to build history representations. Our estimate for the triggering function is equipped with a sigmoid gating mechanism that captures local-in-time triggering effects that are otherwise challenging with standard decaying-over-time kernels. Further, taking both event type representations and temporal embeddings as inputs, the model learns the underlying triggering type-time kernel parameters given pairs of event types. We present experiments on synthetic and real data sets widely used by competing models, while further including a COVID-19 dataset to illustrate a scenario where longitudinal covariates are available. Results show the proposed model outperforms existing approaches while being more efficient in terms of computational complexity and yielding interpretable results via direct application of the newly introduced kernel.

Survival Analysis meets Counterfactual Inference

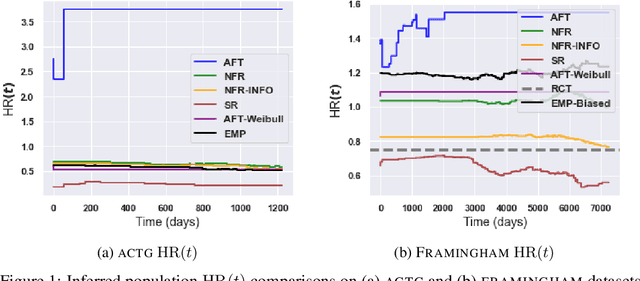
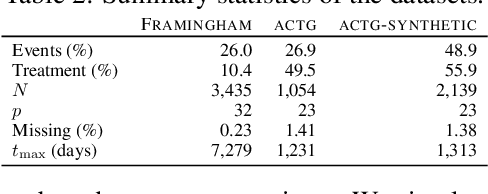
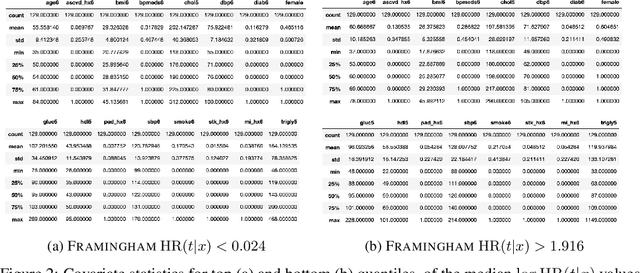
There is growing interest in applying machine learning methods for counterfactual inference from observational data. However, approaches that account for survival outcomes are relatively limited. Survival data are frequently encountered across diverse medical applications, \textit{i.e.}, drug development, risk profiling, and clinical trials, and such data are also relevant in fields like manufacturing (for equipment monitoring). When the outcome of interest is time-to-event, special precautions for handling censored events need to be taken, as ignoring censored outcomes may lead to biased estimates. We propose a theoretically grounded unified framework for counterfactual inference applicable to survival outcomes. Further, we formulate a nonparametric hazard ratio metric for evaluating average and individualized treatment effects. Experimental results on real-world and semi-synthetic datasets, the latter which we introduce, demonstrate that the proposed approach significantly outperforms competitive alternatives in both survival-outcome predictions and treatment-effect estimation.

Survival Cluster Analysis

Conventional survival analysis approaches estimate risk scores or individualized time-to-event distributions conditioned on covariates. In practice, there is often great population-level phenotypic heterogeneity, resulting from (unknown) subpopulations with diverse risk profiles or survival distributions. As a result, there is an unmet need in survival analysis for identifying subpopulations with distinct risk profiles, while jointly accounting for accurate individualized time-to-event predictions. An approach that addresses this need is likely to improve characterization of individual outcomes by leveraging regularities in subpopulations, thus accounting for population-level heterogeneity. In this paper, we propose a Bayesian nonparametrics approach that represents observations (subjects) in a clustered latent space, and encourages accurate time-to-event predictions and clusters (subpopulations) with distinct risk profiles. Experiments on real-world datasets show consistent improvements in predictive performance and interpretability relative to existing state-of-the-art survival analysis models.

Survival Function Matching for Calibrated Time-to-Event Predictions

Models for predicting the time of a future event are crucial for risk assessment, across a diverse range of applications. Existing time-to-event (survival) models have focused primarily on preserving pairwise ordering of estimated event times, or relative risk. Model calibration is relatively under explored, despite its critical importance in time-to-event applications. We present a survival function estimator for probabilistic predictions in time-to-event models, based on a neural network model for draws from the distribution of event times, without explicit assumptions on the form of the distribution. This is done like in adversarial learning, but we achieve learning without a discriminator or adversarial objective. The proposed estimator can be used in practice as a means of estimating and comparing conditional survival distributions, while accounting for the predictive uncertainty of probabilistic models. Extensive experiments show that the proposed model outperforms existing approaches, trained both with and without adversarial learning, in terms of both calibration and concentration of time-to-event distributions.

Adversarial Time-to-Event Modeling

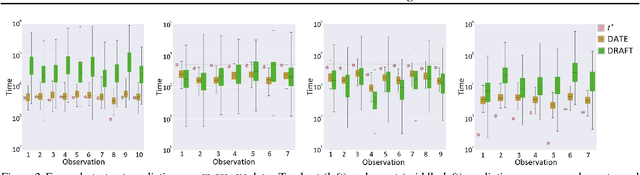
Modern health data science applications leverage abundant molecular and electronic health data, providing opportunities for machine learning to build statistical models to support clinical practice. Time-to-event analysis, also called survival analysis, stands as one of the most representative examples of such statistical models. We present a deep-network-based approach that leverages adversarial learning to address a key challenge in modern time-to-event modeling: nonparametric estimation of event-time distributions. We also introduce a principled cost function to exploit information from censored events (events that occur subsequent to the observation window). Unlike most time-to-event models, we focus on the estimation of time-to-event distributions, rather than time ordering. We validate our model on both benchmark and real datasets, demonstrating that the proposed formulation yields significant performance gains relative to a parametric alternative, which we also propose.

NASH: Toward End-to-End Neural Architecture for Generative Semantic Hashing

Semantic hashing has become a powerful paradigm for fast similarity search in many information retrieval systems. While fairly successful, previous techniques generally require two-stage training, and the binary constraints are handled ad-hoc. In this paper, we present an end-to-end Neural Architecture for Semantic Hashing (NASH), where the binary hashing codes are treated as Bernoulli latent variables. A neural variational inference framework is proposed for training, where gradients are directly back-propagated through the discrete latent variable to optimize the hash function. We also draw connections between proposed method and rate-distortion theory, which provides a theoretical foundation for the effectiveness of the proposed framework. Experimental results on three public datasets demonstrate that our method significantly outperforms several state-of-the-art models on both unsupervised and supervised scenarios.