Beyond Flatland: A Geometric Take on Matching Methods for Treatment Effect Estimation

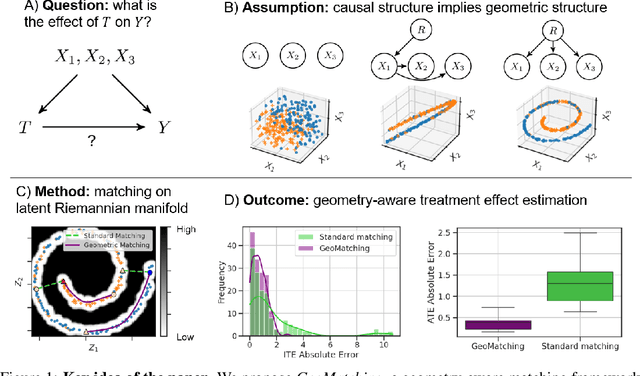
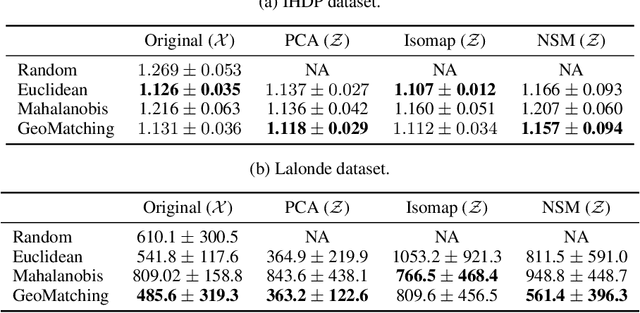
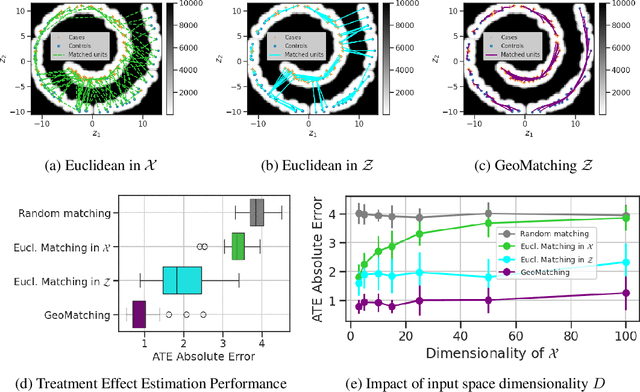
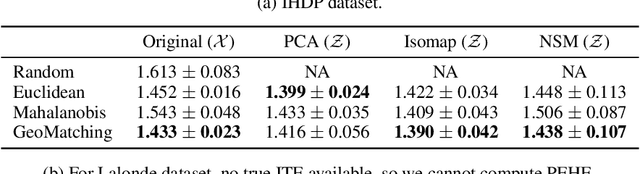
Matching is a popular approach in causal inference to estimate treatment effects by pairing treated and control units that are most similar in terms of their covariate information. However, classic matching methods completely ignore the geometry of the data manifold, which is crucial to define a meaningful distance for matching, and struggle when covariates are noisy and high-dimensional. In this work, we propose GeoMatching, a matching method to estimate treatment effects that takes into account the intrinsic data geometry induced by existing causal mechanisms among the confounding variables. First, we learn a low-dimensional, latent Riemannian manifold that accounts for uncertainty and geometry of the original input data. Second, we estimate treatment effects via matching in the latent space based on the learned latent Riemannian metric. We provide theoretical insights and empirical results in synthetic and real-world scenarios, demonstrating that GeoMatching yields more effective treatment effect estimators, even as we increase input dimensionality, in the presence of outliers, or in semi-supervised scenarios.

AIRIVA: A Deep Generative Model of Adaptive Immune Repertoires

Recent advances in immunomics have shown that T-cell receptor (TCR) signatures can accurately predict active or recent infection by leveraging the high specificity of TCR binding to disease antigens. However, the extreme diversity of the adaptive immune repertoire presents challenges in reliably identifying disease-specific TCRs. Population genetics and sequencing depth can also have strong systematic effects on repertoires, which requires careful consideration when developing diagnostic models. We present an Adaptive Immune Repertoire-Invariant Variational Autoencoder (AIRIVA), a generative model that learns a low-dimensional, interpretable, and compositional representation of TCR repertoires to disentangle such systematic effects in repertoires. We apply AIRIVA to two infectious disease case-studies: COVID-19 (natural infection and vaccination) and the Herpes Simplex Virus (HSV-1 and HSV-2), and empirically show that we can disentangle the individual disease signals. We further demonstrate AIRIVA's capability to: learn from unlabelled samples; generate in-silico TCR repertoires by intervening on the latent factors; and identify disease-associated TCRs validated using TCR annotations from external assay data.

Repairing Neural Networks by Leaving the Right Past Behind

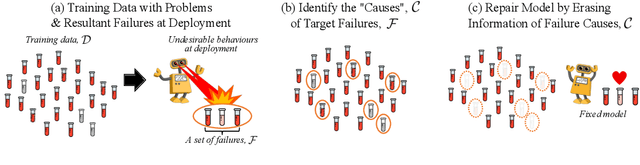
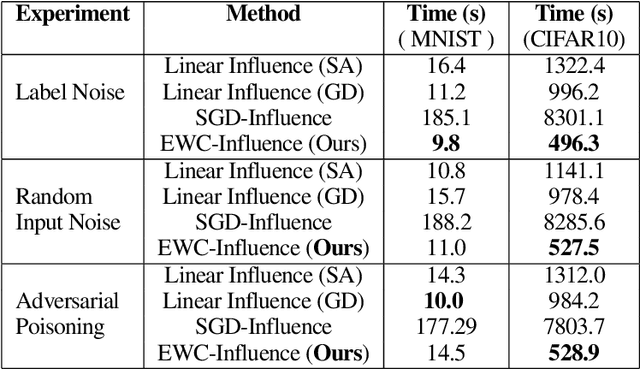
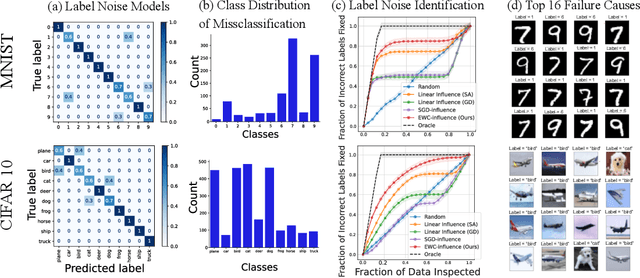
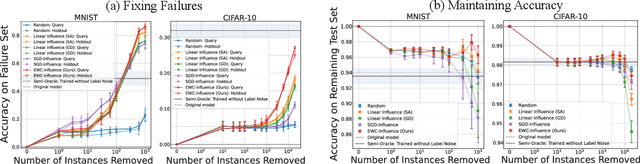
Prediction failures of machine learning models often arise from deficiencies in training data, such as incorrect labels, outliers, and selection biases. However, such data points that are responsible for a given failure mode are generally not known a priori, let alone a mechanism for repairing the failure. This work draws on the Bayesian view of continual learning, and develops a generic framework for both, identifying training examples that have given rise to the target failure, and fixing the model through erasing information about them. This framework naturally allows leveraging recent advances in continual learning to this new problem of model repairment, while subsuming the existing works on influence functions and data deletion as specific instances. Experimentally, the proposed approach outperforms the baselines for both identification of detrimental training data and fixing model failures in a generalisable manner.

Preferential Mixture-of-Experts: Interpretable Models that Rely on Human Expertise as much as Possible

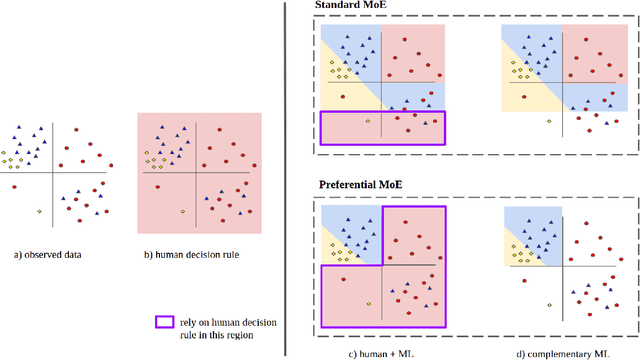
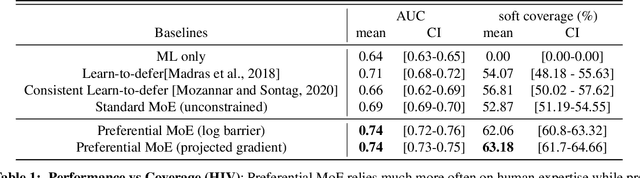
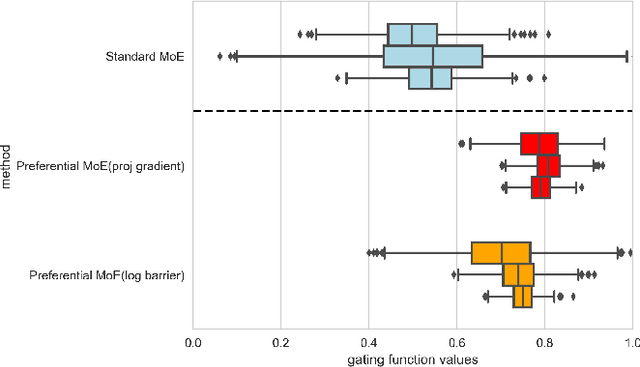
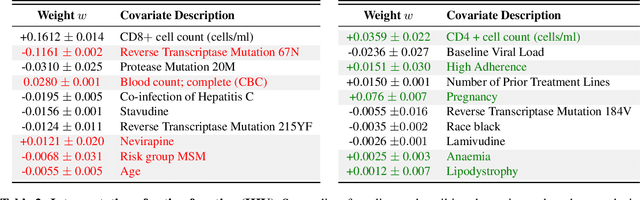
We propose Preferential MoE, a novel human-ML mixture-of-experts model that augments human expertise in decision making with a data-based classifier only when necessary for predictive performance. Our model exhibits an interpretable gating function that provides information on when human rules should be followed or avoided. The gating function is maximized for using human-based rules, and classification errors are minimized. We propose solving a coupled multi-objective problem with convex subproblems. We develop approximate algorithms and study their performance and convergence. Finally, we demonstrate the utility of Preferential MoE on two clinical applications for the treatment of Human Immunodeficiency Virus (HIV) and management of Major Depressive Disorder (MDD).

Towards Expressive Priors for Bayesian Neural Networks: Poisson Process Radial Basis Function Networks

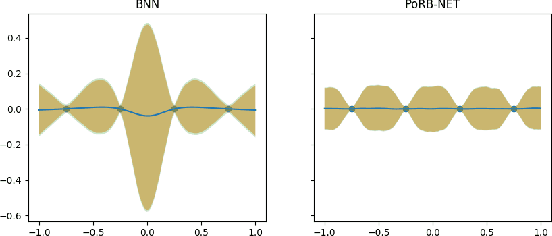
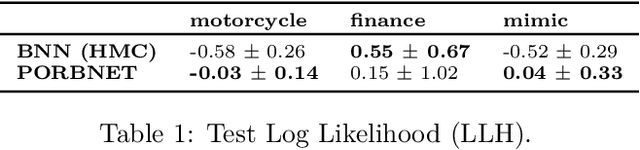
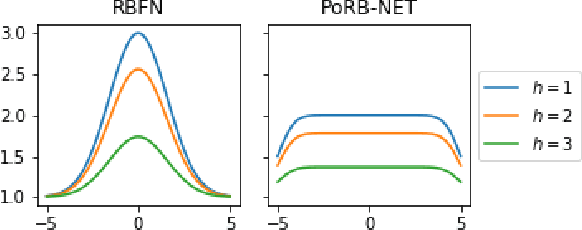
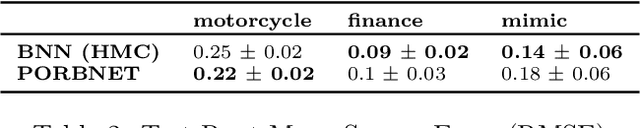
While Bayesian neural networks have many appealing characteristics, current priors do not easily allow users to specify basic properties such as expected lengthscale or amplitude variance. In this work, we introduce Poisson Process Radial Basis Function Networks, a novel prior that is able to encode amplitude stationarity and input-dependent lengthscale. We prove that our novel formulation allows for a decoupled specification of these properties, and that the estimated regression function is consistent as the number of observations tends to infinity. We demonstrate its behavior on synthetic and real examples.

Output-Constrained Bayesian Neural Networks

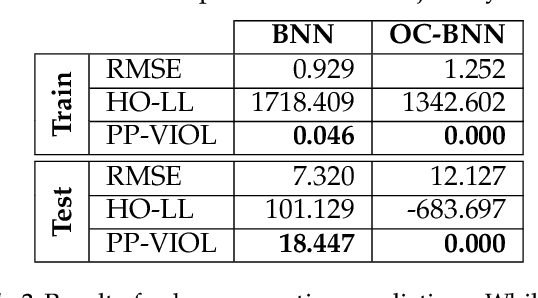
Bayesian neural network (BNN) priors are defined in parameter space, making it hard to encode prior knowledge expressed in function space. We formulate a prior that incorporates functional constraints about what the output can or cannot be in regions of the input space. Output-Constrained BNNs (OC-BNN) represent an interpretable approach of enforcing a range of constraints, fully consistent with the Bayesian framework and amenable to black-box inference. We demonstrate how OC-BNNs improve model robustness and prevent the prediction of infeasible outputs in two real-world applications of healthcare and robotics.

Unsupervised Extraction of Phenotypes from Cancer Clinical Notes for Association Studies

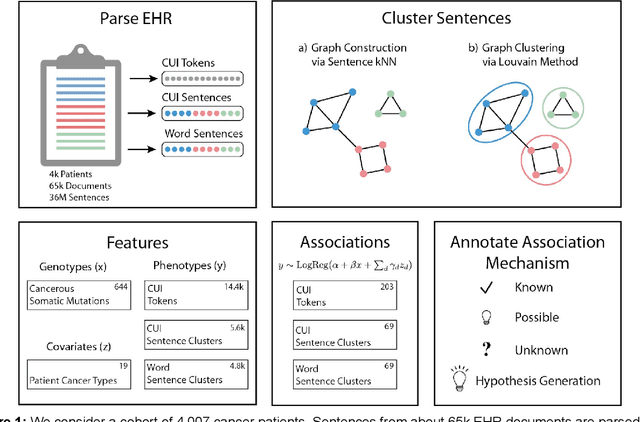
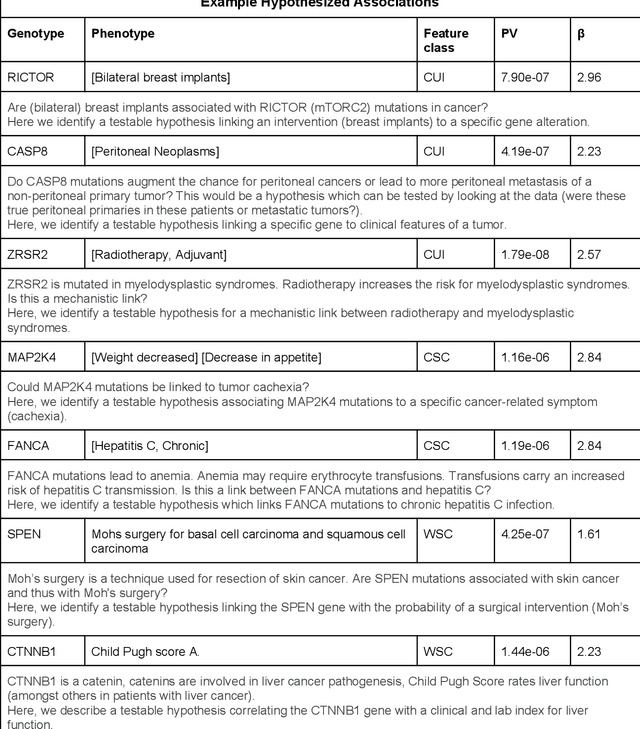
The recent adoption of Electronic Health Records (EHRs) by health care providers has introduced an important source of data that provides detailed and highly specific insights into patient phenotypes over large cohorts. These datasets, in combination with machine learning and statistical approaches, generate new opportunities for research and clinical care. However, many methods require the patient representations to be in structured formats, while the information in the EHR is often locked in unstructured texts designed for human readability. In this work, we develop the methodology to automatically extract clinical features from clinical narratives from large EHR corpora without the need for prior knowledge. We consider medical terms and sentences appearing in clinical narratives as atomic information units. We propose an efficient clustering strategy suitable for the analysis of large text corpora and to utilize the clusters to represent information about the patient compactly. To demonstrate the utility of our approach, we perform an association study of clinical features with somatic mutation profiles from 4,007 cancer patients and their tumors. We apply the proposed algorithm to a dataset consisting of about 65 thousand documents with a total of about 3.2 million sentences. We identify 341 significant statistical associations between the presence of somatic mutations and clinical features. We annotated these associations according to their novelty, and report several known associations. We also propose 32 testable hypotheses where the underlying biological mechanism does not appear to be known but plausible. These results illustrate that the automated discovery of clinical features is possible and the joint analysis of clinical and genetic datasets can generate appealing new hypotheses.

Projected BNNs: Avoiding weight-space pathologies by learning latent representations of neural network weights

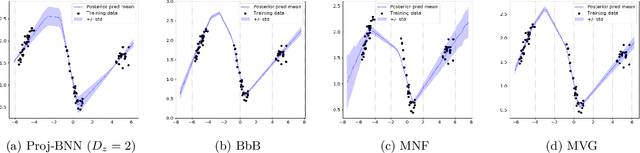
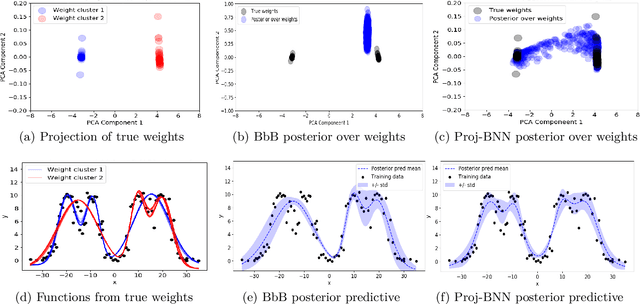
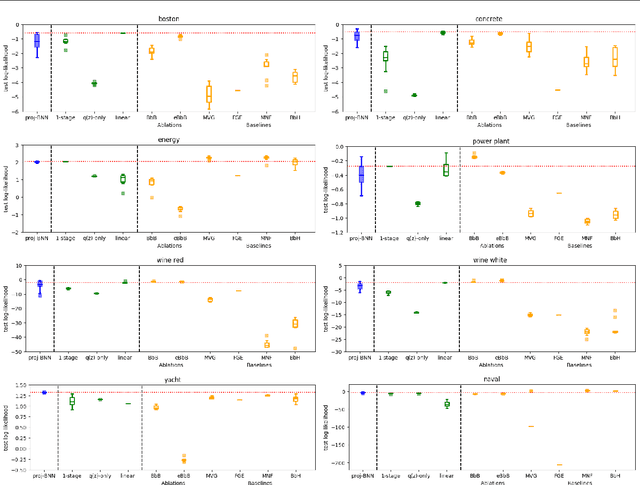
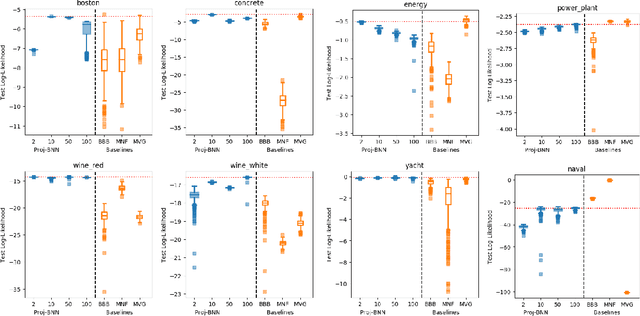
While modern neural networks are making remarkable gains in terms of predictive accuracy, characterizing uncertainty over the parameters of these models (in a Bayesian setting) is challenging because of the high-dimensionality of the network parameter space and the correlations between these parameters. In this paper, we introduce a novel framework for variational inference for Bayesian neural networks that (1) encodes complex distributions in high-dimensional parameter space with representations in a low-dimensional latent space and (2) performs inference efficiently on the low-dimensional representations. Across a large array of synthetic and real-world datasets, we show that our method improves uncertainty characterization and model generalization when compared with methods that work directly in the parameter space.

Sparse Three-parameter Restricted Indian Buffet Process for Understanding International Trade

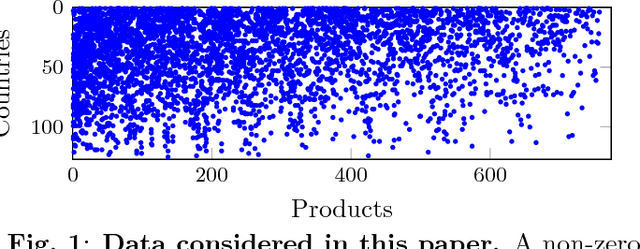
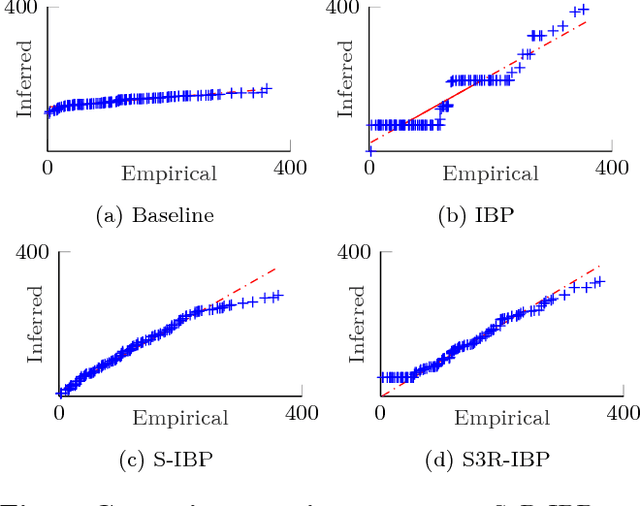
This paper presents a Bayesian nonparametric latent feature model specially suitable for exploratory analysis of high-dimensional count data. We perform a non-negative doubly sparse matrix factorization that has two main advantages: not only we are able to better approximate the row input distributions, but the inferred topics are also easier to interpret. By combining the three-parameter and restricted Indian buffet processes into a single prior, we increase the model flexibility, allowing for a full spectrum of sparse solutions in the latent space. We demonstrate the usefulness of our approach in the analysis of countries' economic structure. Compared to other approaches, empirical results show our model's ability to give easy-to-interpret information and better capture the underlying sparsity structure of data.

General Latent Feature Models for Heterogeneous Datasets

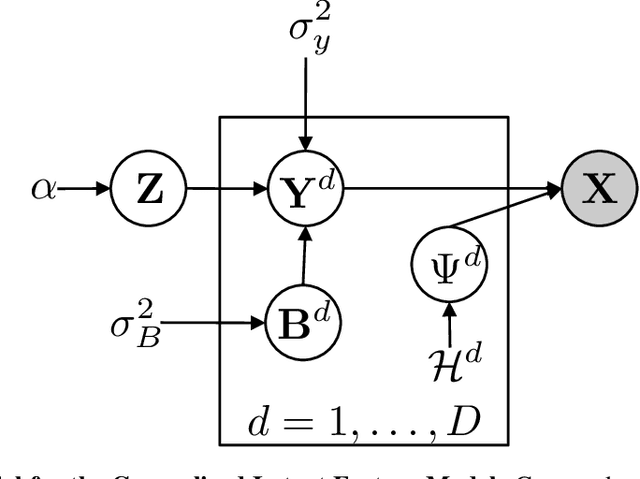
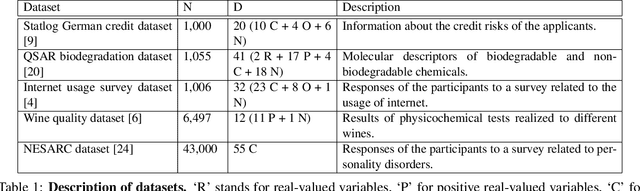
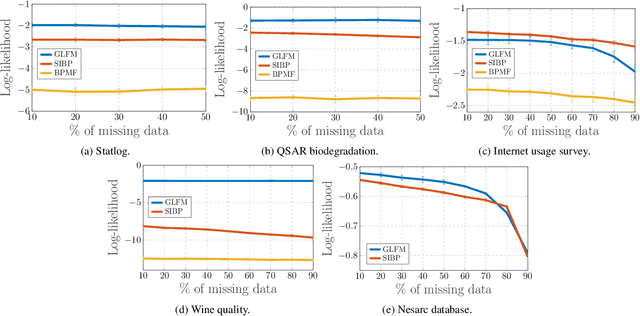
Latent feature modeling allows capturing the latent structure responsible for generating the observed properties of a set of objects. It is often used to make predictions either for new values of interest or missing information in the original data, as well as to perform data exploratory analysis. However, although there is an extensive literature on latent feature models for homogeneous datasets, where all the attributes that describe each object are of the same (continuous or discrete) nature, there is a lack of work on latent feature modeling for heterogeneous databases. In this paper, we introduce a general Bayesian nonparametric latent feature model suitable for heterogeneous datasets, where the attributes describing each object can be either discrete, continuous or mixed variables. The proposed model presents several important properties. First, it accounts for heterogeneous data while keeping the properties of conjugate models, which allow us to infer the model in linear time with respect to the number of objects and attributes. Second, its Bayesian nonparametric nature allows us to automatically infer the model complexity from the data, i.e., the number of features necessary to capture the latent structure in the data. Third, the latent features in the model are binary-valued variables, easing the interpretability of the obtained latent features in data exploratory analysis. We show the flexibility of the proposed model by solving both prediction and data analysis tasks on several real-world datasets. Moreover, a software package of the GLFM is publicly available for other researcher to use and improve it.