Projected BNNs: Avoiding weight-space pathologies by learning latent representations of neural network weights

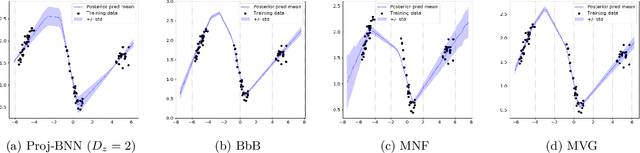
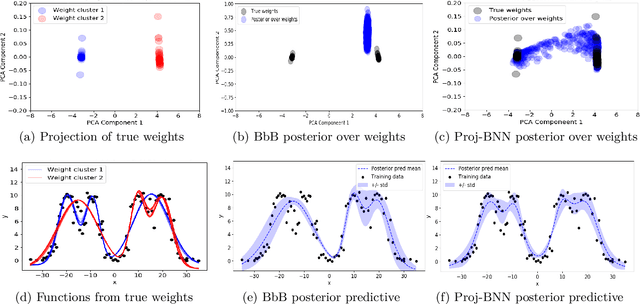
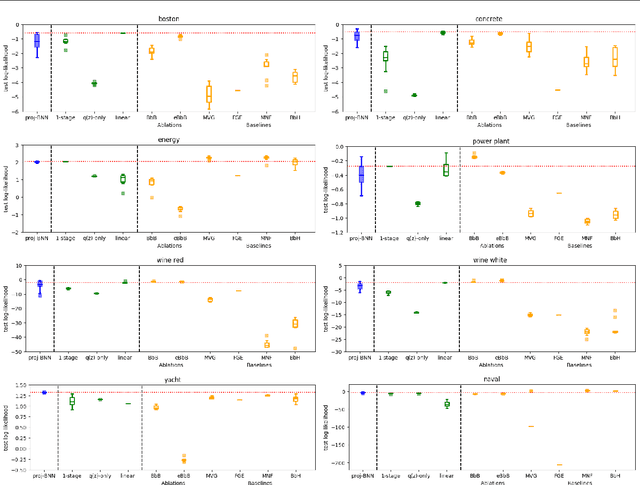
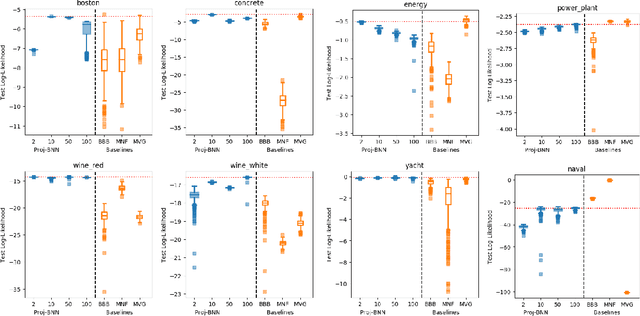
While modern neural networks are making remarkable gains in terms of predictive accuracy, characterizing uncertainty over the parameters of these models (in a Bayesian setting) is challenging because of the high-dimensionality of the network parameter space and the correlations between these parameters. In this paper, we introduce a novel framework for variational inference for Bayesian neural networks that (1) encodes complex distributions in high-dimensional parameter space with representations in a low-dimensional latent space and (2) performs inference efficiently on the low-dimensional representations. Across a large array of synthetic and real-world datasets, we show that our method improves uncertainty characterization and model generalization when compared with methods that work directly in the parameter space.