Reasoning Elicitation in Language Models via Counterfactual Feedback

Despite the increasing effectiveness of language models, their reasoning capabilities remain underdeveloped. In particular, causal reasoning through counterfactual question answering is lacking. This work aims to bridge this gap. We first derive novel metrics that balance accuracy in factual and counterfactual questions, capturing a more complete view of the reasoning abilities of language models than traditional factual-only based metrics. Second, we propose several fine-tuning approaches that aim to elicit better reasoning mechanisms, in the sense of the proposed metrics. Finally, we evaluate the performance of the fine-tuned language models in a variety of realistic scenarios. In particular, we investigate to what extent our fine-tuning approaches systemically achieve better generalization with respect to the base models in several problems that require, among others, inductive and deductive reasoning capabilities.

Beyond Flatland: A Geometric Take on Matching Methods for Treatment Effect Estimation

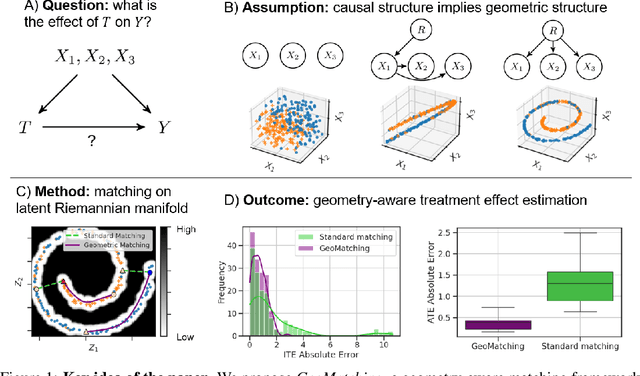
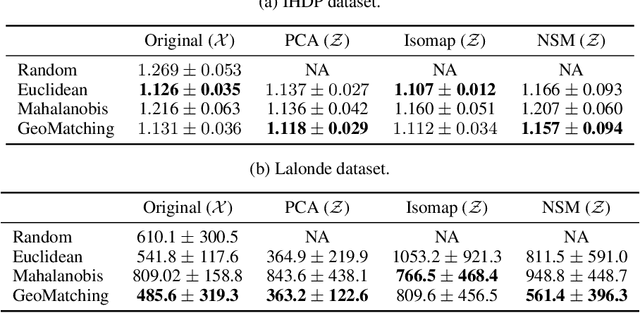
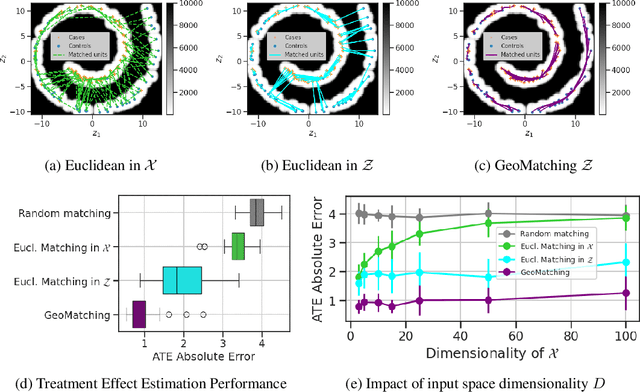
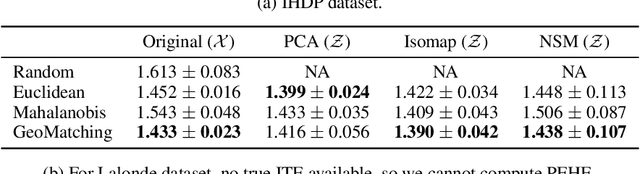
Matching is a popular approach in causal inference to estimate treatment effects by pairing treated and control units that are most similar in terms of their covariate information. However, classic matching methods completely ignore the geometry of the data manifold, which is crucial to define a meaningful distance for matching, and struggle when covariates are noisy and high-dimensional. In this work, we propose GeoMatching, a matching method to estimate treatment effects that takes into account the intrinsic data geometry induced by existing causal mechanisms among the confounding variables. First, we learn a low-dimensional, latent Riemannian manifold that accounts for uncertainty and geometry of the original input data. Second, we estimate treatment effects via matching in the latent space based on the learned latent Riemannian metric. We provide theoretical insights and empirical results in synthetic and real-world scenarios, demonstrating that GeoMatching yields more effective treatment effect estimators, even as we increase input dimensionality, in the presence of outliers, or in semi-supervised scenarios.

Does Reasoning Emerge? Examining the Probabilities of Causation in Large Language Models

Recent advances in AI have been significantly driven by the capabilities of large language models (LLMs) to solve complex problems in ways that resemble human thinking. However, there is an ongoing debate about the extent to which LLMs are capable of actual reasoning. Central to this debate are two key probabilistic concepts that are essential for connecting causes to their effects: the probability of necessity (PN) and the probability of sufficiency (PS). This paper introduces a framework that is both theoretical and practical, aimed at assessing how effectively LLMs are able to replicate real-world reasoning mechanisms using these probabilistic measures. By viewing LLMs as abstract machines that process information through a natural language interface, we examine the conditions under which it is possible to compute suitable approximations of PN and PS. Our research marks an important step towards gaining a deeper understanding of when LLMs are capable of reasoning, as illustrated by a series of math examples.

Beyond Words: A Mathematical Framework for Interpreting Large Language Models

Large language models (LLMs) are powerful AI tools that can generate and comprehend natural language text and other complex information. However, the field lacks a mathematical framework to systematically describe, compare and improve LLMs. We propose Hex a framework that clarifies key terms and concepts in LLM research, such as hallucinations, alignment, self-verification and chain-of-thought reasoning. The Hex framework offers a precise and consistent way to characterize LLMs, identify their strengths and weaknesses, and integrate new findings. Using Hex, we differentiate chain-of-thought reasoning from chain-of-thought prompting and establish the conditions under which they are equivalent. This distinction clarifies the basic assumptions behind chain-of-thought prompting and its implications for methods that use it, such as self-verification and prompt programming. Our goal is to provide a formal framework for LLMs that can help both researchers and practitioners explore new possibilities for generative AI. We do not claim to have a definitive solution, but rather a tool for opening up new research avenues. We argue that our formal definitions and results are crucial for advancing the discussion on how to build generative AI systems that are safe, reliable, fair and robust, especially in domains like healthcare and software engineering.

TRIALSCOPE: A Unifying Causal Framework for Scaling Real-World Evidence Generation with Biomedical Language Models

The rapid digitization of real-world data offers an unprecedented opportunity for optimizing healthcare delivery and accelerating biomedical discovery. In practice, however, such data is most abundantly available in unstructured forms, such as clinical notes in electronic medical records (EMRs), and it is generally plagued by confounders. In this paper, we present TRIALSCOPE, a unifying framework for distilling real-world evidence from population-level observational data. TRIALSCOPE leverages biomedical language models to structure clinical text at scale, employs advanced probabilistic modeling for denoising and imputation, and incorporates state-of-the-art causal inference techniques to combat common confounders. Using clinical trial specification as generic representation, TRIALSCOPE provides a turn-key solution to generate and reason with clinical hypotheses using observational data. In extensive experiments and analyses on a large-scale real-world dataset with over one million cancer patients from a large US healthcare network, we show that TRIALSCOPE can produce high-quality structuring of real-world data and generates comparable results to marquee cancer trials. In addition to facilitating in-silicon clinical trial design and optimization, TRIALSCOPE may be used to empower synthetic controls, pragmatic trials, post-market surveillance, as well as support fine-grained patient-like-me reasoning in precision diagnosis and treatment.

Dynamic Causal Bayesian Optimization

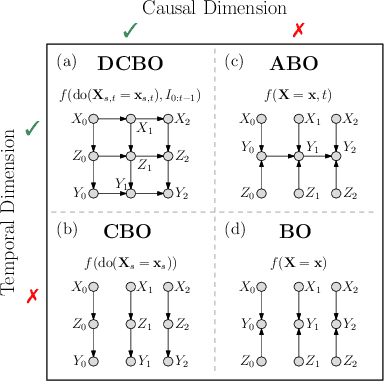
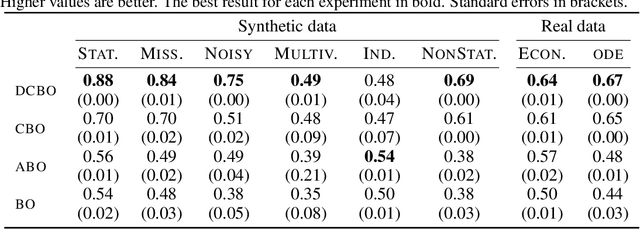
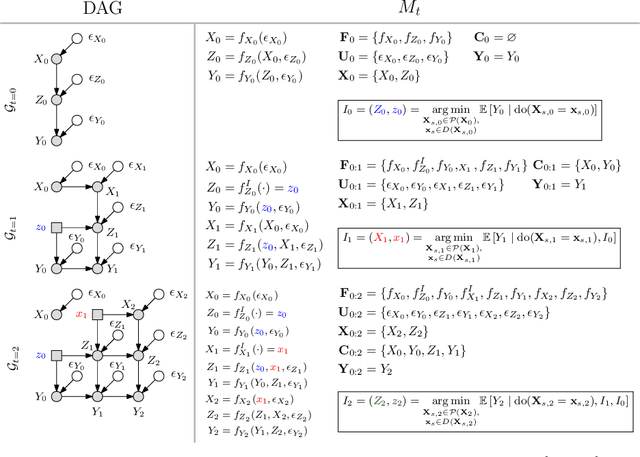
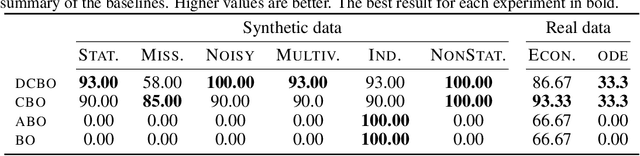
This paper studies the problem of performing a sequence of optimal interventions in a causal dynamical system where both the target variable of interest and the inputs evolve over time. This problem arises in a variety of domains e.g. system biology and operational research. Dynamic Causal Bayesian Optimization (DCBO) brings together ideas from sequential decision making, causal inference and Gaussian process (GP) emulation. DCBO is useful in scenarios where all causal effects in a graph are changing over time. At every time step DCBO identifies a local optimal intervention by integrating both observational and past interventional data collected from the system. We give theoretical results detailing how one can transfer interventional information across time steps and define a dynamic causal GP model which can be used to quantify uncertainty and find optimal interventions in practice. We demonstrate how DCBO identifies optimal interventions faster than competing approaches in multiple settings and applications.

BayesIMP: Uncertainty Quantification for Causal Data Fusion

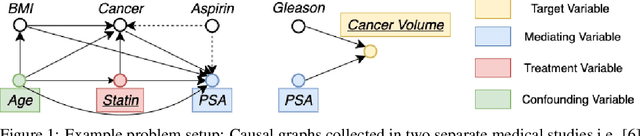
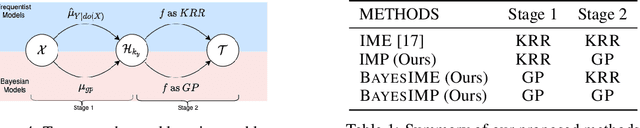
While causal models are becoming one of the mainstays of machine learning, the problem of uncertainty quantification in causal inference remains challenging. In this paper, we study the causal data fusion problem, where datasets pertaining to multiple causal graphs are combined to estimate the average treatment effect of a target variable. As data arises from multiple sources and can vary in quality and quantity, principled uncertainty quantification becomes essential. To that end, we introduce Bayesian Interventional Mean Processes, a framework which combines ideas from probabilistic integration and kernel mean embeddings to represent interventional distributions in the reproducing kernel Hilbert space, while taking into account the uncertainty within each causal graph. To demonstrate the utility of our uncertainty estimation, we apply our method to the Causal Bayesian Optimisation task and show improvements over state-of-the-art methods.

Multi-task Causal Learning with Gaussian Processes

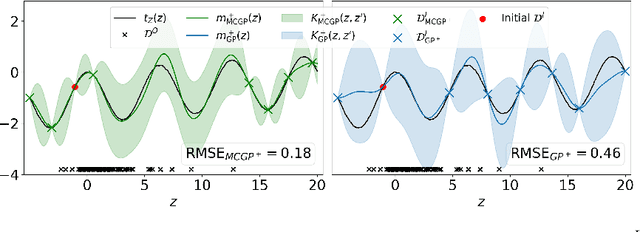
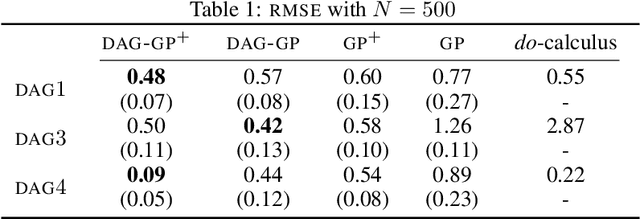
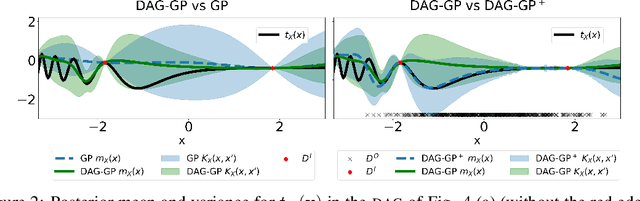
This paper studies the problem of learning the correlation structure of a set of intervention functions defined on the directed acyclic graph (DAG) of a causal model. This is useful when we are interested in jointly learning the causal effects of interventions on different subsets of variables in a DAG, which is common in field such as healthcare or operations research. We propose the first multi-task causal Gaussian process (GP) model, which we call DAG-GP, that allows for information sharing across continuous interventions and across experiments on different variables. DAG-GP accommodates different assumptions in terms of data availability and captures the correlation between functions lying in input spaces of different dimensionality via a well-defined integral operator. We give theoretical results detailing when and how the DAG-GP model can be formulated depending on the DAG. We test both the quality of its predictions and its calibrated uncertainties. Compared to single-task models, DAG-GP achieves the best fitting performance in a variety of real and synthetic settings. In addition, it helps to select optimal interventions faster than competing approaches when used within sequential decision making frameworks, like active learning or Bayesian optimization.

Structure Mapping for Transferability of Causal Models

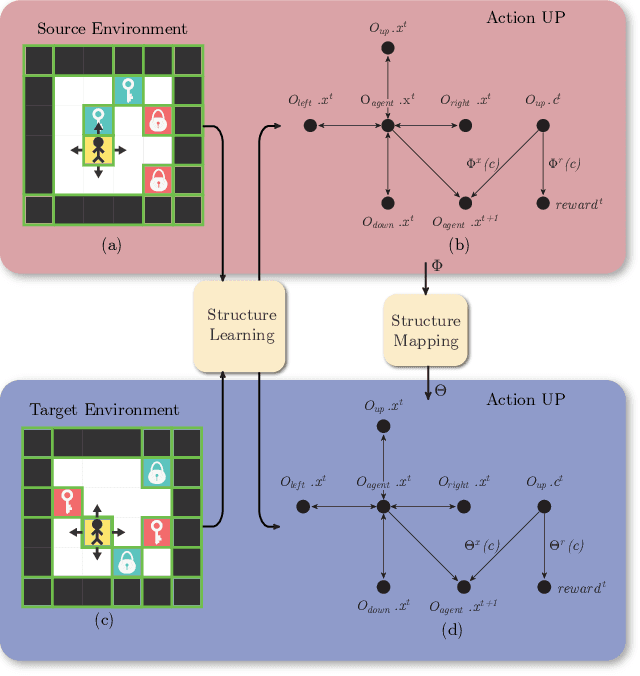
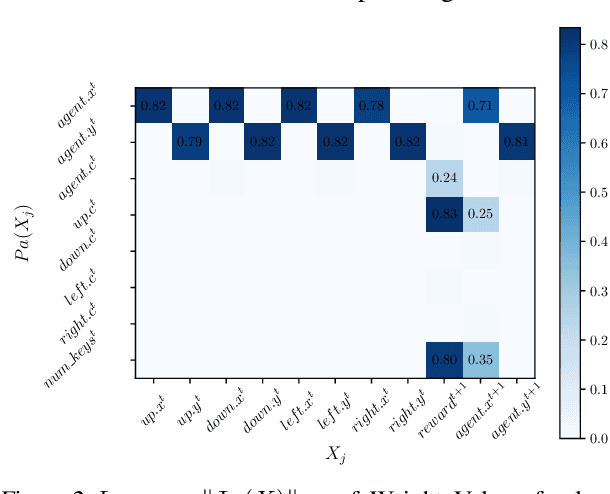
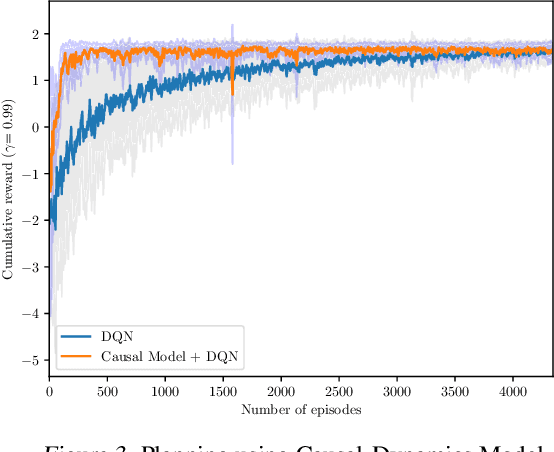
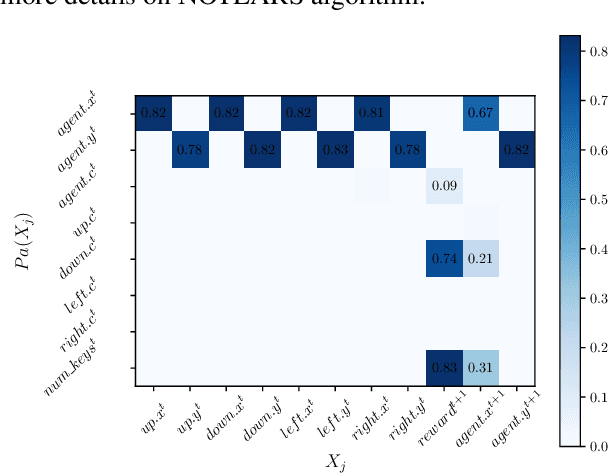
Human beings learn causal models and constantly use them to transfer knowledge between similar environments. We use this intuition to design a transfer-learning framework using object-oriented representations to learn the causal relationships between objects. A learned causal dynamics model can be used to transfer between variants of an environment with exchangeable perceptual features among objects but with the same underlying causal dynamics. We adapt continuous optimization for structure learning techniques to explicitly learn the cause and effects of the actions in an interactive environment and transfer to the target domain by categorization of the objects based on causal knowledge. We demonstrate the advantages of our approach in a gridworld setting by combining causal model-based approach with model-free approach in reinforcement learning.

Learning Inconsistent Preferences with Kernel Methods

We propose a probabilistic kernel approach for preferential learning from pairwise duelling data using Gaussian Processes. Different from previous methods, we do not impose a total order on the item space, hence can capture more expressive latent preferential structures such as inconsistent preferences and clusters of comparable items. Furthermore, we prove the universality of the proposed kernels, i.e. that the corresponding reproducing kernel Hilbert Space (RKHS) is dense in the space of skew-symmetric preference functions. To conclude the paper, we provide an extensive set of numerical experiments on simulated and real-world datasets showcasing the competitiveness of our proposed method with state-of-the-art.