Additive Gaussian Processes Revisited

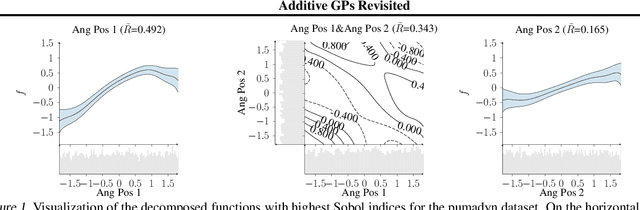
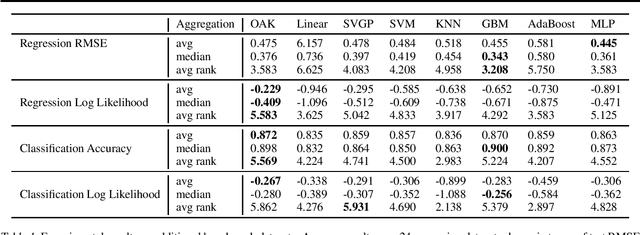
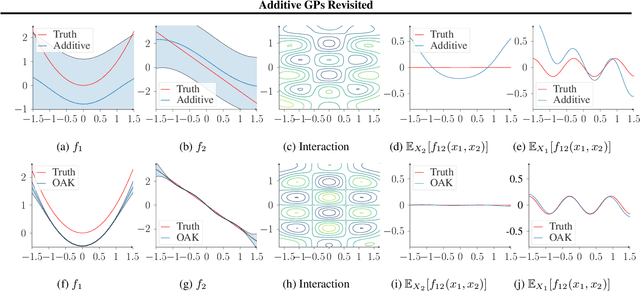
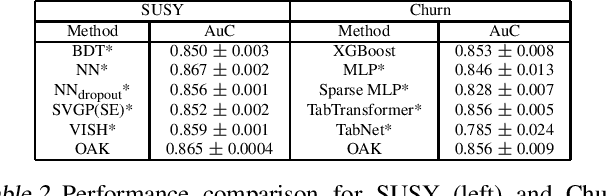
Gaussian Process (GP) models are a class of flexible non-parametric models that have rich representational power. By using a Gaussian process with additive structure, complex responses can be modelled whilst retaining interpretability. Previous work showed that additive Gaussian process models require high-dimensional interaction terms. We propose the orthogonal additive kernel (OAK), which imposes an orthogonality constraint on the additive functions, enabling an identifiable, low-dimensional representation of the functional relationship. We connect the OAK kernel to functional ANOVA decomposition, and show improved convergence rates for sparse computation methods. With only a small number of additive low-dimensional terms, we demonstrate the OAK model achieves similar or better predictive performance compared to black-box models, while retaining interpretability.

Spatially and Robustly Hybrid Mixture Regression Model for Inference of Spatial Dependence

In this paper, we propose a Spatial Robust Mixture Regression model to investigate the relationship between a response variable and a set of explanatory variables over the spatial domain, assuming that the relationships may exhibit complex spatially dynamic patterns that cannot be captured by constant regression coefficients. Our method integrates the robust finite mixture Gaussian regression model with spatial constraints, to simultaneously handle the spatial nonstationarity, local homogeneity, and outlier contaminations. Compared with existing spatial regression models, our proposed model assumes the existence a few distinct regression models that are estimated based on observations that exhibit similar response-predictor relationships. As such, the proposed model not only accounts for nonstationarity in the spatial trend, but also clusters observations into a few distinct and homogenous groups. This provides an advantage on interpretation with a few stationary sub-processes identified that capture the predominant relationships between response and predictor variables. Moreover, the proposed method incorporates robust procedures to handle contaminations from both regression outliers and spatial outliers. By doing so, we robustly segment the spatial domain into distinct local regions with similar regression coefficients, and sporadic locations that are purely outliers. Rigorous statistical hypothesis testing procedure has been designed to test the significance of such segmentation. Experimental results on many synthetic and real-world datasets demonstrate the robustness, accuracy, and effectiveness of our proposed method, compared with other robust finite mixture regression, spatial regression and spatial segmentation methods.

Structure Mapping for Transferability of Causal Models

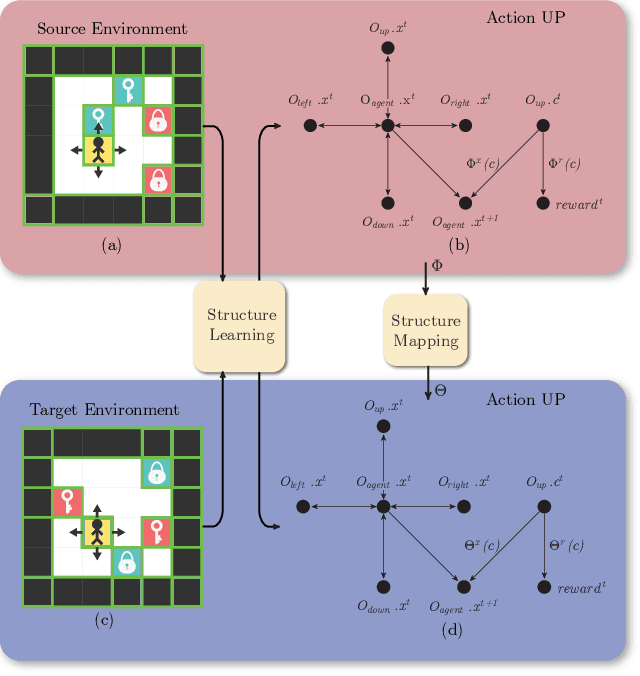
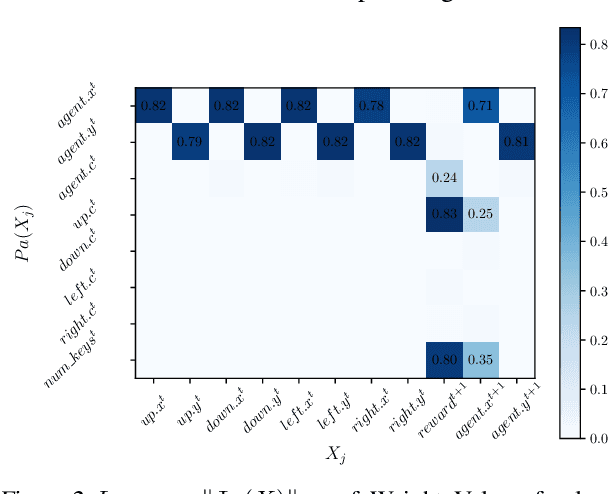
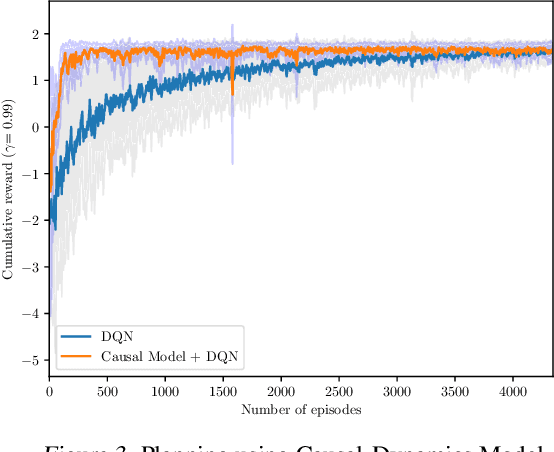
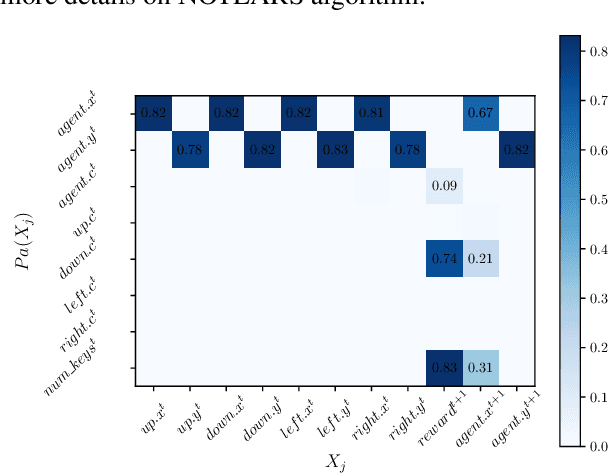
Human beings learn causal models and constantly use them to transfer knowledge between similar environments. We use this intuition to design a transfer-learning framework using object-oriented representations to learn the causal relationships between objects. A learned causal dynamics model can be used to transfer between variants of an environment with exchangeable perceptual features among objects but with the same underlying causal dynamics. We adapt continuous optimization for structure learning techniques to explicitly learn the cause and effects of the actions in an interactive environment and transfer to the target domain by categorization of the objects based on causal knowledge. We demonstrate the advantages of our approach in a gridworld setting by combining causal model-based approach with model-free approach in reinforcement learning.

Causal Bayesian Optimization

This paper studies the problem of globally optimizing a variable of interest that is part of a causal model in which a sequence of interventions can be performed. This problem arises in biology, operational research, communications and, more generally, in all fields where the goal is to optimize an output metric of a system of interconnected nodes. Our approach combines ideas from causal inference, uncertainty quantification and sequential decision making. In particular, it generalizes Bayesian optimization, which treats the input variables of the objective function as independent, to scenarios where causal information is available. We show how knowing the causal graph significantly improves the ability to reason about optimal decision making strategies decreasing the optimization cost while avoiding suboptimal solutions. We propose a new algorithm called Causal Bayesian Optimization (CBO). CBO automatically balances two trade-offs: the classical exploration-exploitation and the new observation-intervention, which emerges when combining real interventional data with the estimated intervention effects computed via do-calculus. We demonstrate the practical benefits of this method in a synthetic setting and in two real-world applications.

On Exploration, Exploitation and Learning in Adaptive Importance Sampling

We study adaptive importance sampling (AIS) as an online learning problem and argue for the importance of the trade-off between exploration and exploitation in this adaptation. Borrowing ideas from the bandits literature, we propose Daisee, a partition-based AIS algorithm. We further introduce a notion of regret for AIS and show that Daisee has $\mathcal{O}(\sqrt{T}(\log T)^{\frac{3}{4}})$ cumulative pseudo-regret, where $T$ is the number of iterations. We then extend Daisee to adaptively learn a hierarchical partitioning of the sample space for more efficient sampling and confirm the performance of both algorithms empirically.

Inference Trees: Adaptive Inference with Exploration

We introduce inference trees (ITs), a new class of inference methods that build on ideas from Monte Carlo tree search to perform adaptive sampling in a manner that balances exploration with exploitation, ensures consistency, and alleviates pathologies in existing adaptive methods. ITs adaptively sample from hierarchical partitions of the parameter space, while simultaneously learning these partitions in an online manner. This enables ITs to not only identify regions of high posterior mass, but also maintain uncertainty estimates to track regions where significant posterior mass may have been missed. ITs can be based on any inference method that provides a consistent estimate of the marginal likelihood. They are particularly effective when combined with sequential Monte Carlo, where they capture long-range dependencies and yield improvements beyond proposal adaptation alone.

Collaborative Filtering with Side Information: a Gaussian Process Perspective

We tackle the problem of collaborative filtering (CF) with side information, through the lens of Gaussian Process (GP) regression. Driven by the idea of using the kernel to explicitly model user-item similarities, we formulate the GP in a way that allows the incorporation of low-rank matrix factorisation, arriving at our model, the Tucker Gaussian Process (TGP). Consequently, TGP generalises classical Bayesian matrix factorisation models, and goes beyond them to give a natural and elegant method for incorporating side information, giving enhanced predictive performance for CF problems. Moreover we show that it is a novel model for regression, especially well-suited to grid-structured data and problems where the dependence on covariates is close to being separable.

Relativistic Monte Carlo

Hamiltonian Monte Carlo (HMC) is a popular Markov chain Monte Carlo (MCMC) algorithm that generates proposals for a Metropolis-Hastings algorithm by simulating the dynamics of a Hamiltonian system. However, HMC is sensitive to large time discretizations and performs poorly if there is a mismatch between the spatial geometry of the target distribution and the scales of the momentum distribution. In particular the mass matrix of HMC is hard to tune well. In order to alleviate these problems we propose relativistic Hamiltonian Monte Carlo, a version of HMC based on relativistic dynamics that introduce a maximum velocity on particles. We also derive stochastic gradient versions of the algorithm and show that the resulting algorithms bear interesting relationships to gradient clipping, RMSprop, Adagrad and Adam, popular optimisation methods in deep learning. Based on this, we develop relativistic stochastic gradient descent by taking the zero-temperature limit of relativistic stochastic gradient Hamiltonian Monte Carlo. In experiments we show that the relativistic algorithms perform better than classical Newtonian variants and Adam.