Spatially and Robustly Hybrid Mixture Regression Model for Inference of Spatial Dependence

In this paper, we propose a Spatial Robust Mixture Regression model to investigate the relationship between a response variable and a set of explanatory variables over the spatial domain, assuming that the relationships may exhibit complex spatially dynamic patterns that cannot be captured by constant regression coefficients. Our method integrates the robust finite mixture Gaussian regression model with spatial constraints, to simultaneously handle the spatial nonstationarity, local homogeneity, and outlier contaminations. Compared with existing spatial regression models, our proposed model assumes the existence a few distinct regression models that are estimated based on observations that exhibit similar response-predictor relationships. As such, the proposed model not only accounts for nonstationarity in the spatial trend, but also clusters observations into a few distinct and homogenous groups. This provides an advantage on interpretation with a few stationary sub-processes identified that capture the predominant relationships between response and predictor variables. Moreover, the proposed method incorporates robust procedures to handle contaminations from both regression outliers and spatial outliers. By doing so, we robustly segment the spatial domain into distinct local regions with similar regression coefficients, and sporadic locations that are purely outliers. Rigorous statistical hypothesis testing procedure has been designed to test the significance of such segmentation. Experimental results on many synthetic and real-world datasets demonstrate the robustness, accuracy, and effectiveness of our proposed method, compared with other robust finite mixture regression, spatial regression and spatial segmentation methods.

Denoising individual bias for a fairer binary submatrix detection

Low rank representation of binary matrix is powerful in disentangling sparse individual-attribute associations, and has received wide applications. Existing binary matrix factorization (BMF) or co-clustering (CC) methods often assume i.i.d background noise. However, this assumption could be easily violated in real data, where heterogeneous row- or column-wise probability of binary entries results in disparate element-wise background distribution, and paralyzes the rationality of existing methods. We propose a binary data denoising framework, namely BIND, which optimizes the detection of true patterns by estimating the row- or column-wise mixture distribution of patterns and disparate background, and eliminating the binary attributes that are more likely from the background. BIND is supported by thoroughly derived mathematical property of the row- and column-wise mixture distributions. Our experiment on synthetic and real-world data demonstrated BIND effectively removes background noise and drastically increases the fairness and accuracy of state-of-the arts BMF and CC methods.

Geometric All-Way Boolean Tensor Decomposition

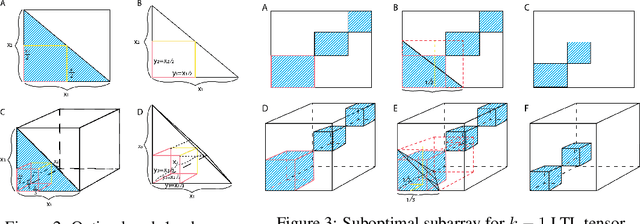
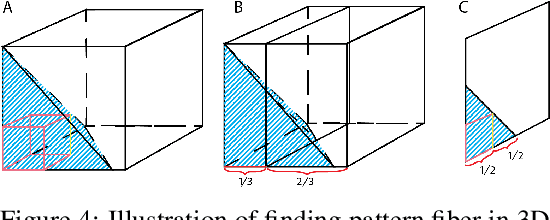
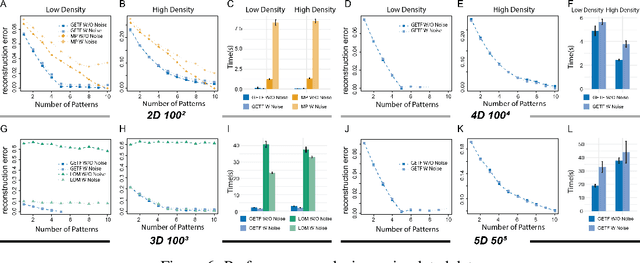
Boolean tensor has been broadly utilized in representing high dimensional logical data collected on spatial, temporal and/or other relational domains. Boolean Tensor Decomposition (BTD) factorizes a binary tensor into the Boolean sum of multiple rank-1 tensors, which is an NP-hard problem. Existing BTD methods have been limited by their high computational cost, in applications to large scale or higher order tensors. In this work, we presented a computationally efficient BTD algorithm, namely \textit{Geometric Expansion for all-order Tensor Factorization} (GETF), that sequentially identifies the rank-1 basis components for a tensor from a geometric perspective. We conducted rigorous theoretical analysis on the validity as well as algorithemic efficiency of GETF in decomposing all-order tensor. Experiments on both synthetic and real-world data demonstrated that GETF has significantly improved performance in reconstruction accuracy, extraction of latent structures and it is an order of magnitude faster than other state-of-the-art methods.

Supervised clustering of high dimensional data using regularized mixture modeling

Identifying relationships between molecular variations and their clinical presentations has been challenged by the heterogeneous causes of a disease. It is imperative to unveil the relationship between the high dimensional molecular manifestations and the clinical presentations, while taking into account the possible heterogeneity of the study subjects. We proposed a novel supervised clustering algorithm using penalized mixture regression model, called CSMR, to deal with the challenges in studying the heterogeneous relationships between high dimensional molecular features to a phenotype. The algorithm was adapted from the classification expectation maximization algorithm, which offers a novel supervised solution to the clustering problem, with substantial improvement on both the computational efficiency and biological interpretability. Experimental evaluation on simulated benchmark datasets demonstrated that the CSMR can accurately identify the subspaces on which subset of features are explanatory to the response variables, and it outperformed the baseline methods. Application of CSMR on a drug sensitivity dataset again demonstrated the superior performance of CSMR over the others, where CSMR is powerful in recapitulating the distinct subgroups hidden in the pool of cell lines with regards to their coping mechanisms to different drugs. CSMR represents a big data analysis tool with the potential to resolve the complexity of translating the clinical manifestations of the disease to the real causes underpinning it. We believe that it will bring new understanding to the molecular basis of a disease, and could be of special relevance in the growing field of personalized medicine.

A New Algorithm using Component-wise Adaptive Trimming For Robust Mixture Regression

Mixture regression provides a statistical model for teasing out latent heterogeneous relationships between response and independent variables. Solving mixture regression relying on EM algorithm is highly sensitive to outliers. To enable simultaneous outlier detection and robust parameter estimation, we proposed a fast and efficient robust mixture regression algorithm, considering Component-wise Adaptive Trimming (CAT). Compared with multiple existing algorithms, it grasps a good balance of computational efficiency and robustness, in different scenarios of simulated data, where unequal component proportions and variances, different levels of outlier contaminations and sample sizes, occur. The adaptive trimming ability of CAT makes it a highly potential tool for mining the latent relationships among variables in the big data era. CAT has been implemented in an R package 'RobMixReg' available in CRAN.

MEBF: a fast and efficient Boolean matrix factorization method

Boolean matrix has been used to represent digital information in many fields, including bank transaction, crime records, natural language processing, protein-protein interaction, etc. Boolean matrix factorization (BMF) aims to find an approximation of a binary matrix as the Boolean product of two low rank Boolean matrices, which could generate vast amount of information for the patterns of relationships between the features and samples. Inspired by binary matrix permutation theories and geometric segmentation, we developed a fast and efficient BMF approach called MEBF (Median Expansion for Boolean Factorization). Overall, MEBF adopted a heuristic approach to locate binary patterns presented as submatrices that are dense in 1's. At each iteration, MEBF permutates the rows and columns such that the permutated matrix is approximately Upper Triangular-Like (UTL) with so-called Simultaneous Consecutive-ones Property (SC1P). The largest submatrix dense in 1 would lies on the upper triangular area of the permutated matrix, and its location was determined based on a geometric segmentation of a triangular. We compared MEBF with other state of the art approaches on data scenarios with different sparsity and noise levels. MEBF demonstrated superior performances in lower reconstruction error, and higher computational efficiency, as well as more accurate sparse patterns than popular methods such as ASSO, PANDA and MP. We demonstrated the application of MEBF on both binary and non-binary data sets, and revealed its further potential in knowledge retrieving and data denoising.