Aditya V. Nori
RE-IMAGINE: Symbolic Benchmark Synthesis for Reasoning Evaluation
Jun 18, 2025Abstract:Recent Large Language Models (LLMs) have reported high accuracy on reasoning benchmarks. However, it is still unclear whether the observed results arise from true reasoning or from statistical recall of the training set. Inspired by the ladder of causation (Pearl, 2009) and its three levels (associations, interventions and counterfactuals), this paper introduces RE-IMAGINE, a framework to characterize a hierarchy of reasoning ability in LLMs, alongside an automated pipeline to generate problem variations at different levels of the hierarchy. By altering problems in an intermediate symbolic representation, RE-IMAGINE generates arbitrarily many problems that are not solvable using memorization alone. Moreover, the framework is general and can work across reasoning domains, including math, code, and logic. We demonstrate our framework on four widely-used benchmarks to evaluate several families of LLMs, and observe reductions in performance when the models are queried with problem variations. These assessments indicate a degree of reliance on statistical recall for past performance, and open the door to further research targeting skills across the reasoning hierarchy.
Compositional Causal Reasoning Evaluation in Language Models
Mar 06, 2025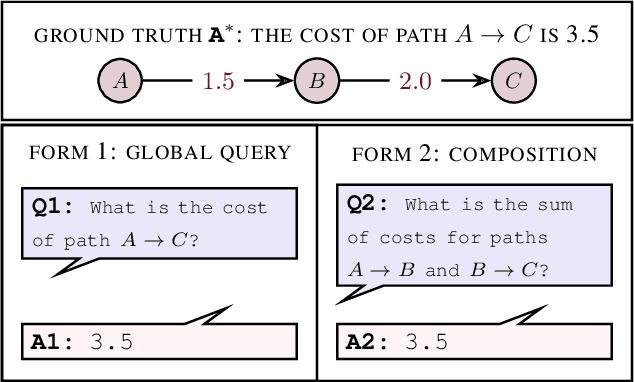

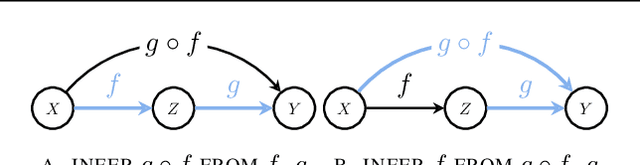

Abstract:Causal reasoning and compositional reasoning are two core aspirations in generative AI. Measuring the extent of these behaviors requires principled evaluation methods. We explore a unified perspective that considers both behaviors simultaneously, termed compositional causal reasoning (CCR): the ability to infer how causal measures compose and, equivalently, how causal quantities propagate through graphs. We instantiate a framework for the systematic evaluation of CCR for the average treatment effect and the probability of necessity and sufficiency. As proof of concept, we demonstrate the design of CCR tasks for language models in the LLama, Phi, and GPT families. On a math word problem, our framework revealed a range of taxonomically distinct error patterns. Additionally, CCR errors increased with the complexity of causal paths for all models except o1.
Reasoning Elicitation in Language Models via Counterfactual Feedback
Oct 02, 2024



Abstract:Despite the increasing effectiveness of language models, their reasoning capabilities remain underdeveloped. In particular, causal reasoning through counterfactual question answering is lacking. This work aims to bridge this gap. We first derive novel metrics that balance accuracy in factual and counterfactual questions, capturing a more complete view of the reasoning abilities of language models than traditional factual-only based metrics. Second, we propose several fine-tuning approaches that aim to elicit better reasoning mechanisms, in the sense of the proposed metrics. Finally, we evaluate the performance of the fine-tuned language models in a variety of realistic scenarios. In particular, we investigate to what extent our fine-tuning approaches systemically achieve better generalization with respect to the base models in several problems that require, among others, inductive and deductive reasoning capabilities.
Does Reasoning Emerge? Examining the Probabilities of Causation in Large Language Models
Aug 15, 2024Abstract:Recent advances in AI have been significantly driven by the capabilities of large language models (LLMs) to solve complex problems in ways that resemble human thinking. However, there is an ongoing debate about the extent to which LLMs are capable of actual reasoning. Central to this debate are two key probabilistic concepts that are essential for connecting causes to their effects: the probability of necessity (PN) and the probability of sufficiency (PS). This paper introduces a framework that is both theoretical and practical, aimed at assessing how effectively LLMs are able to replicate real-world reasoning mechanisms using these probabilistic measures. By viewing LLMs as abstract machines that process information through a natural language interface, we examine the conditions under which it is possible to compute suitable approximations of PN and PS. Our research marks an important step towards gaining a deeper understanding of when LLMs are capable of reasoning, as illustrated by a series of math examples.
Beyond Words: A Mathematical Framework for Interpreting Large Language Models
Nov 06, 2023Abstract:Large language models (LLMs) are powerful AI tools that can generate and comprehend natural language text and other complex information. However, the field lacks a mathematical framework to systematically describe, compare and improve LLMs. We propose Hex a framework that clarifies key terms and concepts in LLM research, such as hallucinations, alignment, self-verification and chain-of-thought reasoning. The Hex framework offers a precise and consistent way to characterize LLMs, identify their strengths and weaknesses, and integrate new findings. Using Hex, we differentiate chain-of-thought reasoning from chain-of-thought prompting and establish the conditions under which they are equivalent. This distinction clarifies the basic assumptions behind chain-of-thought prompting and its implications for methods that use it, such as self-verification and prompt programming. Our goal is to provide a formal framework for LLMs that can help both researchers and practitioners explore new possibilities for generative AI. We do not claim to have a definitive solution, but rather a tool for opening up new research avenues. We argue that our formal definitions and results are crucial for advancing the discussion on how to build generative AI systems that are safe, reliable, fair and robust, especially in domains like healthcare and software engineering.
Exploring the Boundaries of GPT-4 in Radiology
Oct 23, 2023



Abstract:The recent success of general-domain large language models (LLMs) has significantly changed the natural language processing paradigm towards a unified foundation model across domains and applications. In this paper, we focus on assessing the performance of GPT-4, the most capable LLM so far, on the text-based applications for radiology reports, comparing against state-of-the-art (SOTA) radiology-specific models. Exploring various prompting strategies, we evaluated GPT-4 on a diverse range of common radiology tasks and we found GPT-4 either outperforms or is on par with current SOTA radiology models. With zero-shot prompting, GPT-4 already obtains substantial gains ($\approx$ 10% absolute improvement) over radiology models in temporal sentence similarity classification (accuracy) and natural language inference ($F_1$). For tasks that require learning dataset-specific style or schema (e.g. findings summarisation), GPT-4 improves with example-based prompting and matches supervised SOTA. Our extensive error analysis with a board-certified radiologist shows GPT-4 has a sufficient level of radiology knowledge with only occasional errors in complex context that require nuanced domain knowledge. For findings summarisation, GPT-4 outputs are found to be overall comparable with existing manually-written impressions.
Robustness of Neural Networks: A Probabilistic and Practical Approach
Feb 15, 2019Abstract:Neural networks are becoming increasingly prevalent in software, and it is therefore important to be able to verify their behavior. Because verifying the correctness of neural networks is extremely challenging, it is common to focus on the verification of other properties of these systems. One important property, in particular, is robustness. Most existing definitions of robustness, however, focus on the worst-case scenario where the inputs are adversarial. Such notions of robustness are too strong, and unlikely to be satisfied by-and verifiable for-practical neural networks. Observing that real-world inputs to neural networks are drawn from non-adversarial probability distributions, we propose a novel notion of robustness: probabilistic robustness, which requires the neural network to be robust with at least $(1 - \epsilon)$ probability with respect to the input distribution. This probabilistic approach is practical and provides a principled way of estimating the robustness of a neural network. We also present an algorithm, based on abstract interpretation and importance sampling, for checking whether a neural network is probabilistically robust. Our algorithm uses abstract interpretation to approximate the behavior of a neural network and compute an overapproximation of the input regions that violate robustness. It then uses importance sampling to counter the effect of such overapproximation and compute an accurate estimate of the probability that the neural network violates the robustness property.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge