Compositional Causal Reasoning Evaluation in Language Models

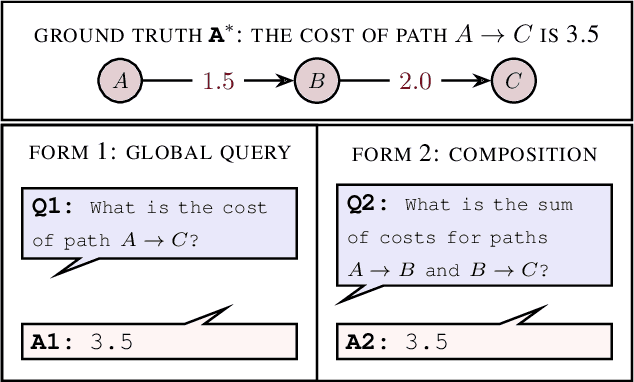
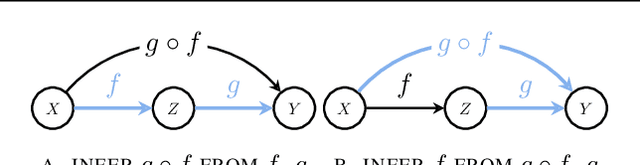
Causal reasoning and compositional reasoning are two core aspirations in generative AI. Measuring the extent of these behaviors requires principled evaluation methods. We explore a unified perspective that considers both behaviors simultaneously, termed compositional causal reasoning (CCR): the ability to infer how causal measures compose and, equivalently, how causal quantities propagate through graphs. We instantiate a framework for the systematic evaluation of CCR for the average treatment effect and the probability of necessity and sufficiency. As proof of concept, we demonstrate the design of CCR tasks for language models in the LLama, Phi, and GPT families. On a math word problem, our framework revealed a range of taxonomically distinct error patterns. Additionally, CCR errors increased with the complexity of causal paths for all models except o1.

Hybrid Global Causal Discovery with Local Search

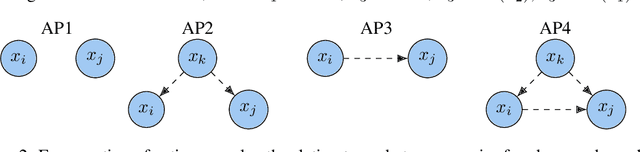
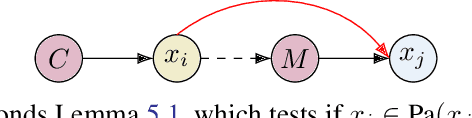
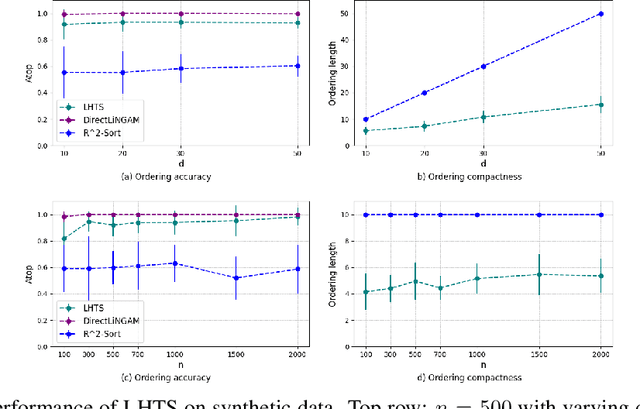
Learning the unique directed acyclic graph corresponding to an unknown causal model is a challenging task. Methods based on functional causal models can identify a unique graph, but either suffer from the curse of dimensionality or impose strong parametric assumptions. To address these challenges, we propose a novel hybrid approach for global causal discovery in observational data that leverages local causal substructures. We first present a topological sorting algorithm that leverages ancestral relationships in linear structural equation models to establish a compact top-down hierarchical ordering, encoding more causal information than linear orderings produced by existing methods. We demonstrate that this approach generalizes to nonlinear settings with arbitrary noise. We then introduce a nonparametric constraint-based algorithm that prunes spurious edges by searching for local conditioning sets, achieving greater accuracy than current methods. We provide theoretical guarantees for correctness and worst-case polynomial time complexities, with empirical validation on synthetic data.

Regularized Data Programming with Bayesian Priors

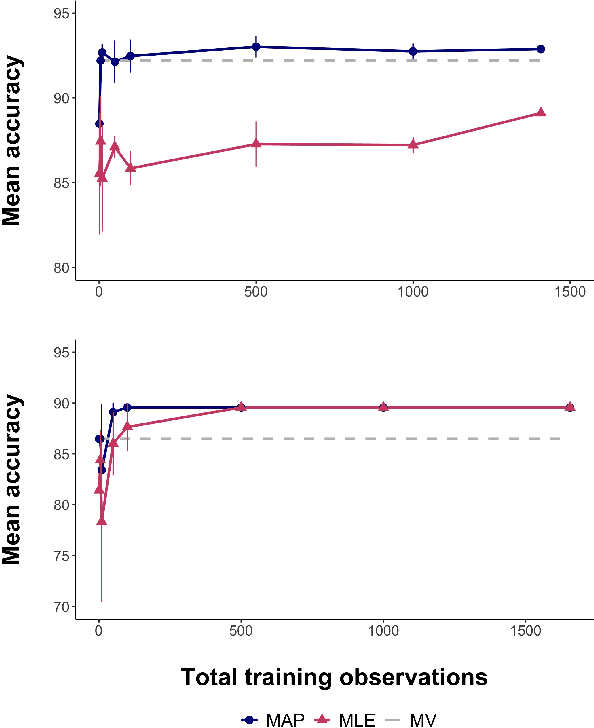
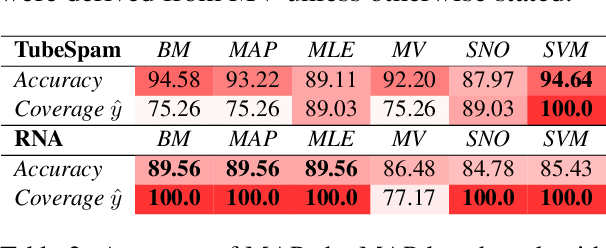
The cost of manual data labeling can be a significant obstacle in supervised learning. Data programming (DP) offers a weakly supervised solution for training dataset creation, wherein the outputs of user-defined programmatic labeling functions (LFs) are reconciled through unsupervised learning. However, DP can fail to outperform an unweighted majority vote in some scenarios, including low-data contexts. This work introduces a Bayesian extension of classical DP that mitigates failures of unsupervised learning by augmenting the DP objective with regularization terms. Regularized learning is achieved through maximum a posteriori estimation in the Bayesian model. Results suggest that regularized DP improves performance relative to maximum likelihood and majority voting, confers greater interpretability, and bolsters performance in low-data regimes.