AIRIVA: A Deep Generative Model of Adaptive Immune Repertoires

Recent advances in immunomics have shown that T-cell receptor (TCR) signatures can accurately predict active or recent infection by leveraging the high specificity of TCR binding to disease antigens. However, the extreme diversity of the adaptive immune repertoire presents challenges in reliably identifying disease-specific TCRs. Population genetics and sequencing depth can also have strong systematic effects on repertoires, which requires careful consideration when developing diagnostic models. We present an Adaptive Immune Repertoire-Invariant Variational Autoencoder (AIRIVA), a generative model that learns a low-dimensional, interpretable, and compositional representation of TCR repertoires to disentangle such systematic effects in repertoires. We apply AIRIVA to two infectious disease case-studies: COVID-19 (natural infection and vaccination) and the Herpes Simplex Virus (HSV-1 and HSV-2), and empirically show that we can disentangle the individual disease signals. We further demonstrate AIRIVA's capability to: learn from unlabelled samples; generate in-silico TCR repertoires by intervening on the latent factors; and identify disease-associated TCRs validated using TCR annotations from external assay data.

Invariant Priors for Bayesian Quadrature

Bayesian quadrature (BQ) is a model-based numerical integration method that is able to increase sample efficiency by encoding and leveraging known structure of the integration task at hand. In this paper, we explore priors that encode invariance of the integrand under a set of bijective transformations in the input domain, in particular some unitary transformations, such as rotations, axis-flips, or point symmetries. We show initial results on superior performance in comparison to standard Bayesian quadrature on several synthetic and one real world application.

Emulation of physical processes with Emukit

Decision making in uncertain scenarios is an ubiquitous challenge in real world systems. Tools to deal with this challenge include simulations to gather information and statistical emulation to quantify uncertainty. The machine learning community has developed a number of methods to facilitate decision making, but so far they are scattered in multiple different toolkits, and generally rely on a fixed backend. In this paper, we present Emukit, a highly adaptable Python toolkit for enriching decision making under uncertainty. Emukit allows users to: (i) use state of the art methods including Bayesian optimization, multi-fidelity emulation, experimental design, Bayesian quadrature and sensitivity analysis; (ii) easily prototype new decision making methods for new problems. Emukit is agnostic to the underlying modeling framework and enables users to use their own custom models. We show how Emukit can be used on three exemplary case studies.

RKHS-SHAP: Shapley Values for Kernel Methods

Feature attribution for kernel methods is often heuristic and not individualised for each prediction. To address this, we turn to the concept of Shapley values, a coalition game theoretical framework that has previously been applied to different machine learning model interpretation tasks, such as linear models, tree ensembles and deep networks. By analysing Shapley values from a functional perspective, we propose \textsc{RKHS-SHAP}, an attribution method for kernel machines that can efficiently compute both \emph{Interventional} and \emph{Observational Shapley values} using kernel mean embeddings of distributions. We show theoretically that our method is robust with respect to local perturbations - a key yet often overlooked desideratum for interpretability. Further, we propose \emph{Shapley regulariser}, applicable to a general empirical risk minimisation framework, allowing learning while controlling the level of specific feature's contributions to the model. We demonstrate that the Shapley regulariser enables learning which is robust to covariate shift of a given feature and fair learning which controls the Shapley values of sensitive features.

GIBBON: General-purpose Information-Based Bayesian OptimisatioN

This paper describes a general-purpose extension of max-value entropy search, a popular approach for Bayesian Optimisation (BO). A novel approximation is proposed for the information gain -- an information-theoretic quantity central to solving a range of BO problems, including noisy, multi-fidelity and batch optimisations across both continuous and highly-structured discrete spaces. Previously, these problems have been tackled separately within information-theoretic BO, each requiring a different sophisticated approximation scheme, except for batch BO, for which no computationally-lightweight information-theoretic approach has previously been proposed. GIBBON (General-purpose Information-Based Bayesian OptimisatioN) provides a single principled framework suitable for all the above, out-performing existing approaches whilst incurring substantially lower computational overheads. In addition, GIBBON does not require the problem's search space to be Euclidean and so is the first high-performance yet computationally light-weight acquisition function that supports batch BO over general highly structured input spaces like molecular search and gene design. Moreover, our principled derivation of GIBBON yields a natural interpretation of a popular batch BO heuristic based on determinantal point processes. Finally, we analyse GIBBON across a suite of synthetic benchmark tasks, a molecular search loop, and as part of a challenging batch multi-fidelity framework for problems with controllable experimental noise.

Good practices for Bayesian Optimization of high dimensional structured spaces

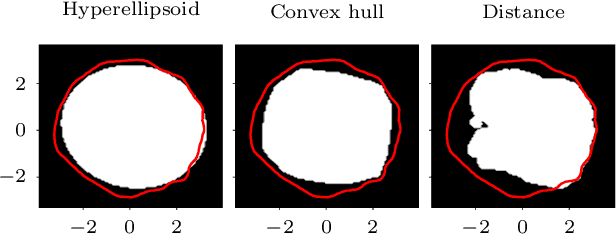
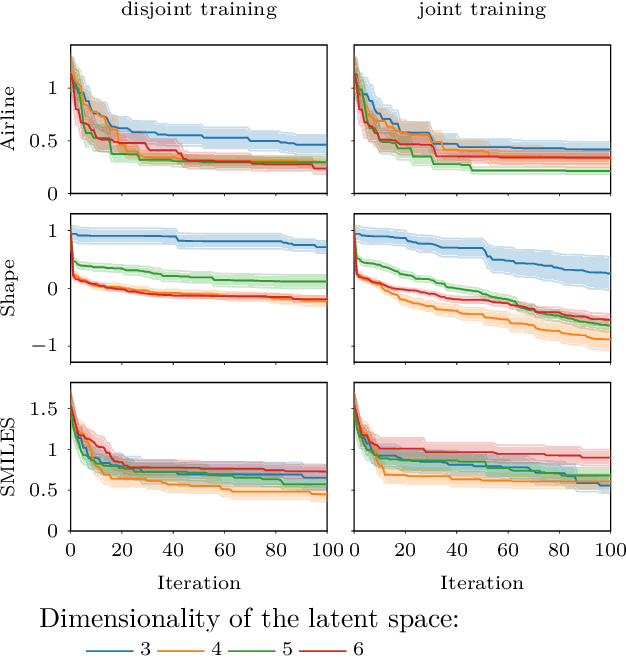
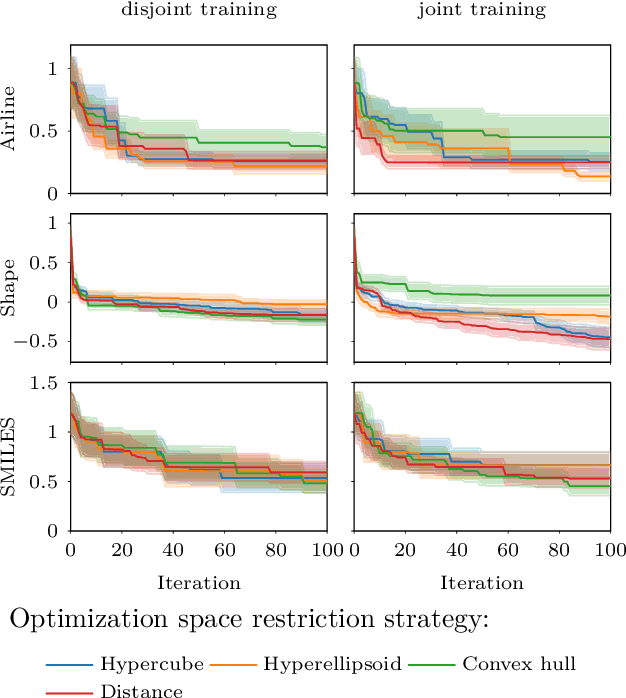
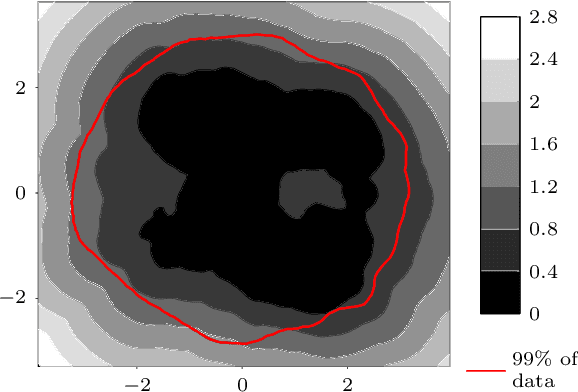
The increasing availability of structured but high dimensional data has opened new opportunities for optimization. One emerging and promising avenue is the exploration of unsupervised methods for projecting structured high dimensional data into low dimensional continuous representations, simplifying the optimization problem and enabling the application of traditional optimization methods. However, this line of research has been purely methodological with little connection to the needs of practitioners so far. In this paper, we study the effect of different search space design choices for performing Bayesian Optimization in high dimensional structured datasets. In particular, we analyse the influence of the dimensionality of the latent space, the role of the acquisition function and evaluate new methods to automatically define the optimization bounds in the latent space. Finally, based on experimental results using synthetic and real datasets, we provide recommendations for the practitioners.

BOSS: Bayesian Optimization over String Spaces

This article develops a Bayesian optimization (BO) method which acts directly over raw strings, proposing the first uses of string kernels and genetic algorithms within BO loops. Recent applications of BO over strings have been hindered by the need to map inputs into a smooth and unconstrained latent space. Learning this projection is computationally and data-intensive. Our approach instead builds a powerful Gaussian process surrogate model based on string kernels, naturally supporting variable length inputs, and performs efficient acquisition function maximization for spaces with syntactical constraints. Experiments demonstrate considerably improved optimization over existing approaches across a broad range of constraints, including the popular setting where syntax is governed by a context-free grammar.

Preferential Batch Bayesian Optimization

Most research in Bayesian optimization (BO) has focused on direct feedback scenarios, where one has access to exact, or perturbed, values of some expensive-to-evaluate objective. This direction has been mainly driven by the use of BO in machine learning hyper-parameter configuration problems. However, in domains such as modelling human preferences, A/B tests or recommender systems, there is a need of methods that are able to replace direct feedback with preferential feedback, obtained via rankings or pairwise comparisons. In this work, we present Preferential Batch Bayesian Optimization (PBBO), a new framework that allows to find the optimum of a latent function of interest, given any type of parallel preferential feedback for a group of two or more points. We do so by using a Gaussian process model with a likelihood specially designed to enable parallel and efficient data collection mechanisms, which are key in modern machine learning. We show how the acquisitions developed under this framework generalize and augment previous approaches in Bayesian optimization, expanding the use of these techniques to a wider range of domains. An extensive simulation study shows the benefits of this approach, both with simulated functions and four real data sets.

Efficient nonmyopic Bayesian optimization and quadrature

Finite-horizon sequential decision problems arise naturally in many machine learning contexts, including Bayesian optimization and Bayesian quadrature. Computing the optimal policy for such problems requires solving Bellman equations, which are generally intractable. Most existing work resorts to myopic approximations by limiting the decision horizon to only a single time-step, which can perform poorly at balancing exploration and exploitation. We propose a general framework for efficient, nonmyopic approximation of the optimal policy by drawing a connection between the optimal adaptive policy and its non-adaptive counterpart. Our proposal is to compute an optimal batch of points, then select a single point from within this batch to evaluate. We realize this idea for both Bayesian optimization and Bayesian quadrature and demonstrate that our proposed method significantly outperforms common myopic alternatives on a variety of tasks.

Meta-Surrogate Benchmarking for Hyperparameter Optimization

Despite the recent progress in hyperparameter optimization (HPO), available benchmarks that resemble real-world scenarios consist of a few and very large problem instances that are expensive to solve. This blocks researchers and practitioners not only from systematically running large-scale comparisons that are needed to draw statistically significant results but also from reproducing experiments that were conducted before. This work proposes a method to alleviate these issues by means of a meta-surrogate model for HPO tasks trained on off-line generated data. The model combines a probabilistic encoder with a multi-task model such that it can generate inexpensive and realistic tasks of the class of problems of interest. We demonstrate that benchmarking HPO methods on samples of the generative model allows us to draw more coherent and statistically significant conclusions that can be reached orders of magnitude faster than using the original tasks. We provide evidence of our findings for various HPO methods on a wide class of problems.