Kernel Quantile Embeddings and Associated Probability Metrics

Embedding probability distributions into reproducing kernel Hilbert spaces (RKHS) has enabled powerful nonparametric methods such as the maximum mean discrepancy (MMD), a statistical distance with strong theoretical and computational properties. At its core, the MMD relies on kernel mean embeddings to represent distributions as mean functions in RKHS. However, it remains unclear if the mean function is the only meaningful RKHS representation. Inspired by generalised quantiles, we introduce the notion of kernel quantile embeddings (KQEs). We then use KQEs to construct a family of distances that: (i) are probability metrics under weaker kernel conditions than MMD; (ii) recover a kernelised form of the sliced Wasserstein distance; and (iii) can be efficiently estimated with near-linear cost. Through hypothesis testing, we show that these distances offer a competitive alternative to MMD and its fast approximations.

Nested Expectations with Kernel Quadrature

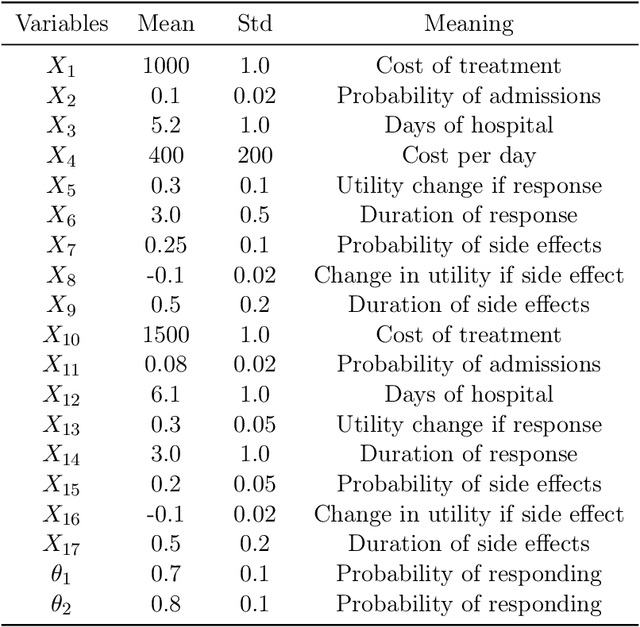
This paper considers the challenging computational task of estimating nested expectations. Existing algorithms, such as nested Monte Carlo or multilevel Monte Carlo, are known to be consistent but require a large number of samples at both inner and outer levels to converge. Instead, we propose a novel estimator consisting of nested kernel quadrature estimators and we prove that it has a faster convergence rate than all baseline methods when the integrands have sufficient smoothness. We then demonstrate empirically that our proposed method does indeed require fewer samples to estimate nested expectations on real-world applications including Bayesian optimisation, option pricing, and health economics.

Conditional Bayesian Quadrature

We propose a novel approach for estimating conditional or parametric expectations in the setting where obtaining samples or evaluating integrands is costly. Through the framework of probabilistic numerical methods (such as Bayesian quadrature), our novel approach allows to incorporates prior information about the integrands especially the prior smoothness knowledge about the integrands and the conditional expectation. As a result, our approach provides a way of quantifying uncertainty and leads to a fast convergence rate, which is confirmed both theoretically and empirically on challenging tasks in Bayesian sensitivity analysis, computational finance and decision making under uncertainty.

Optimally-Weighted Estimators of the Maximum Mean Discrepancy for Likelihood-Free Inference

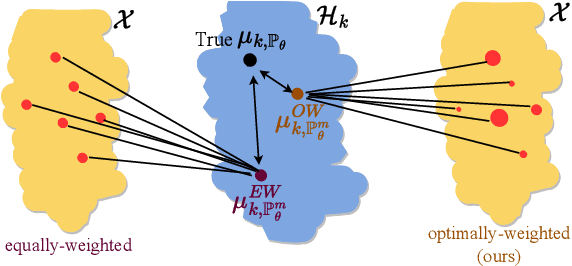
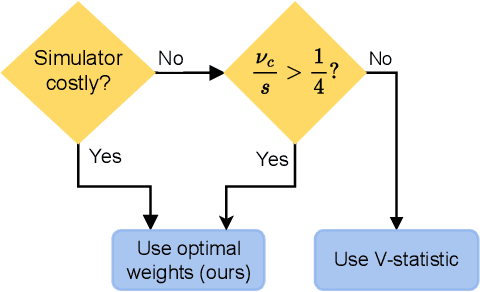
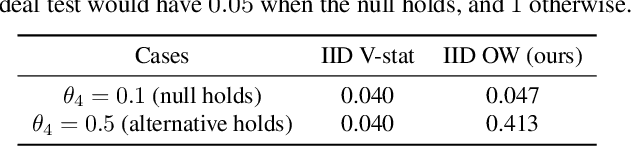
Likelihood-free inference methods typically make use of a distance between simulated and real data. A common example is the maximum mean discrepancy (MMD), which has previously been used for approximate Bayesian computation, minimum distance estimation, generalised Bayesian inference, and within the nonparametric learning framework. The MMD is commonly estimated at a root-$m$ rate, where $m$ is the number of simulated samples. This can lead to significant computational challenges since a large $m$ is required to obtain an accurate estimate, which is crucial for parameter estimation. In this paper, we propose a novel estimator for the MMD with significantly improved sample complexity. The estimator is particularly well suited for computationally expensive smooth simulators with low- to mid-dimensional inputs. This claim is supported through both theoretical results and an extensive simulation study on benchmark simulators.

Invariant Priors for Bayesian Quadrature

Bayesian quadrature (BQ) is a model-based numerical integration method that is able to increase sample efficiency by encoding and leveraging known structure of the integration task at hand. In this paper, we explore priors that encode invariance of the integrand under a set of bijective transformations in the input domain, in particular some unitary transformations, such as rotations, axis-flips, or point symmetries. We show initial results on superior performance in comparison to standard Bayesian quadrature on several synthetic and one real world application.

Using Pairwise Occurrence Information to Improve Knowledge Graph Completion on Large-Scale Datasets

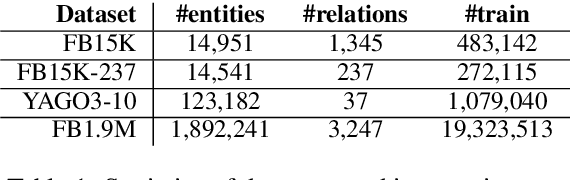
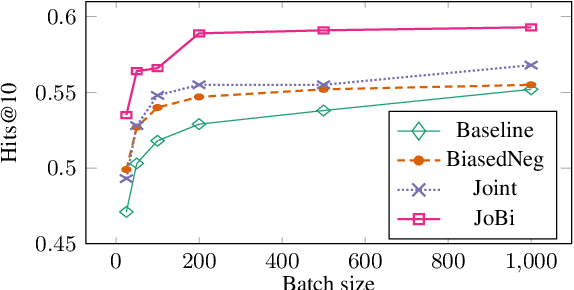
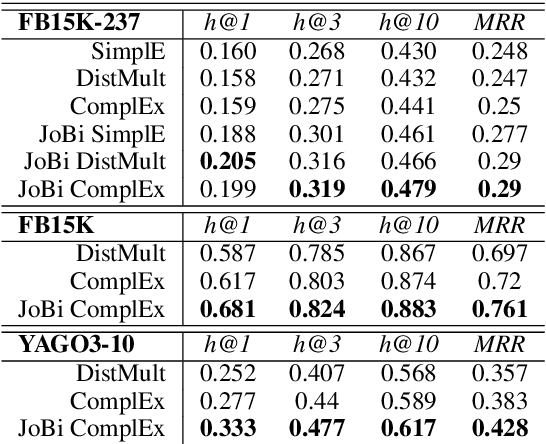
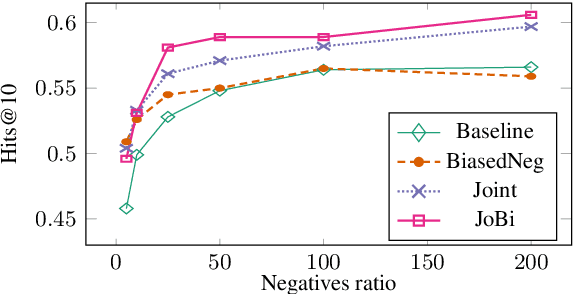
Bilinear models such as DistMult and ComplEx are effective methods for knowledge graph (KG) completion. However, they require large batch sizes, which becomes a performance bottleneck when training on large scale datasets due to memory constraints. In this paper we use occurrences of entity-relation pairs in the dataset to construct a joint learning model and to increase the quality of sampled negatives during training. We show on three standard datasets that when these two techniques are combined, they give a significant improvement in performance, especially when the batch size and the number of generated negative examples are low relative to the size of the dataset. We then apply our techniques to a dataset containing 2 million entities and demonstrate that our model outperforms the baseline by 2.8% absolute on hits@1.