Nested Expectations with Kernel Quadrature

This paper considers the challenging computational task of estimating nested expectations. Existing algorithms, such as nested Monte Carlo or multilevel Monte Carlo, are known to be consistent but require a large number of samples at both inner and outer levels to converge. Instead, we propose a novel estimator consisting of nested kernel quadrature estimators and we prove that it has a faster convergence rate than all baseline methods when the integrands have sufficient smoothness. We then demonstrate empirically that our proposed method does indeed require fewer samples to estimate nested expectations on real-world applications including Bayesian optimisation, option pricing, and health economics.

Conditional Bayesian Quadrature

We propose a novel approach for estimating conditional or parametric expectations in the setting where obtaining samples or evaluating integrands is costly. Through the framework of probabilistic numerical methods (such as Bayesian quadrature), our novel approach allows to incorporates prior information about the integrands especially the prior smoothness knowledge about the integrands and the conditional expectation. As a result, our approach provides a way of quantifying uncertainty and leads to a fast convergence rate, which is confirmed both theoretically and empirically on challenging tasks in Bayesian sensitivity analysis, computational finance and decision making under uncertainty.

Conformal Counterfactual Inference under Hidden Confounding

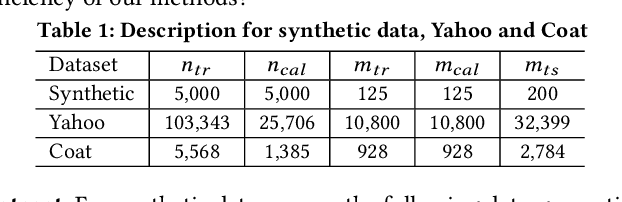
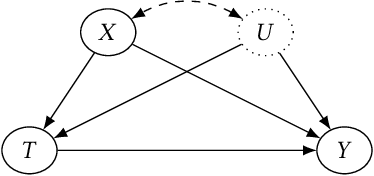
Personalized decision making requires the knowledge of potential outcomes under different treatments, and confidence intervals about the potential outcomes further enrich this decision-making process and improve its reliability in high-stakes scenarios. Predicting potential outcomes along with its uncertainty in a counterfactual world poses the foundamental challenge in causal inference. Existing methods that construct confidence intervals for counterfactuals either rely on the assumption of strong ignorability, or need access to un-identifiable lower and upper bounds that characterize the difference between observational and interventional distributions. To overcome these limitations, we first propose a novel approach wTCP-DR based on transductive weighted conformal prediction, which provides confidence intervals for counterfactual outcomes with marginal converage guarantees, even under hidden confounding. With less restrictive assumptions, our approach requires access to a fraction of interventional data (from randomized controlled trials) to account for the covariate shift from observational distributoin to interventional distribution. Theoretical results explicitly demonstrate the conditions under which our algorithm is strictly advantageous to the naive method that only uses interventional data. After ensuring valid intervals on counterfactuals, it is straightforward to construct intervals for individual treatment effects (ITEs). We demonstrate our method across synthetic and real-world data, including recommendation systems, to verify the superiority of our methods compared against state-of-the-art baselines in terms of both coverage and efficiency

Tractable Function-Space Variational Inference in Bayesian Neural Networks

Reliable predictive uncertainty estimation plays an important role in enabling the deployment of neural networks to safety-critical settings. A popular approach for estimating the predictive uncertainty of neural networks is to define a prior distribution over the network parameters, infer an approximate posterior distribution, and use it to make stochastic predictions. However, explicit inference over neural network parameters makes it difficult to incorporate meaningful prior information about the data-generating process into the model. In this paper, we pursue an alternative approach. Recognizing that the primary object of interest in most settings is the distribution over functions induced by the posterior distribution over neural network parameters, we frame Bayesian inference in neural networks explicitly as inferring a posterior distribution over functions and propose a scalable function-space variational inference method that allows incorporating prior information and results in reliable predictive uncertainty estimates. We show that the proposed method leads to state-of-the-art uncertainty estimation and predictive performance on a range of prediction tasks and demonstrate that it performs well on a challenging safety-critical medical diagnosis task in which reliable uncertainty estimation is essential.

PanoViT: Vision Transformer for Room Layout Estimation from a Single Panoramic Image

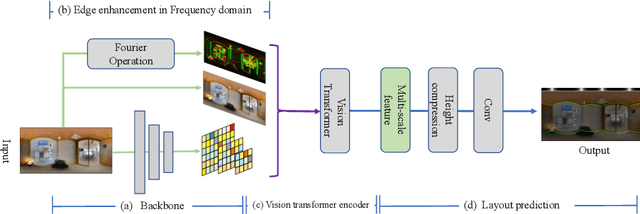
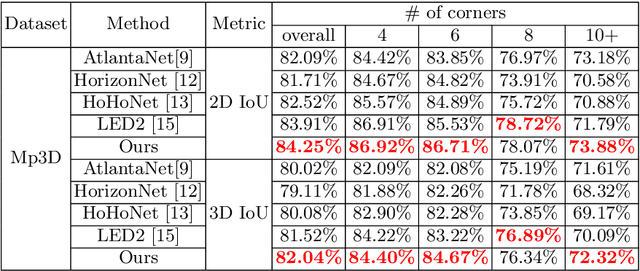
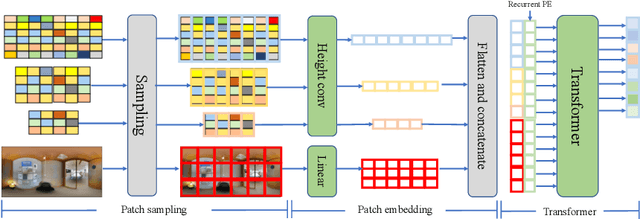
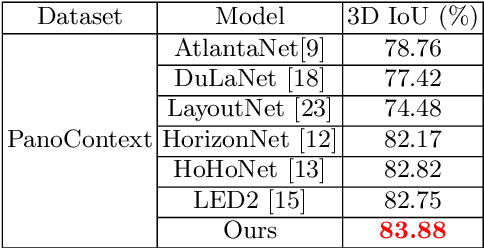
In this paper, we propose PanoViT, a panorama vision transformer to estimate the room layout from a single panoramic image. Compared to CNN models, our PanoViT is more proficient in learning global information from the panoramic image for the estimation of complex room layouts. Considering the difference between a perspective image and an equirectangular image, we design a novel recurrent position embedding and a patch sampling method for the processing of panoramic images. In addition to extracting global information, PanoViT also includes a frequency-domain edge enhancement module and a 3D loss to extract local geometric features in a panoramic image. Experimental results on several datasets demonstrate that our method outperforms state-of-the-art solutions in room layout prediction accuracy.

Efficient Neural Network Training via Forward and Backward Propagation Sparsification

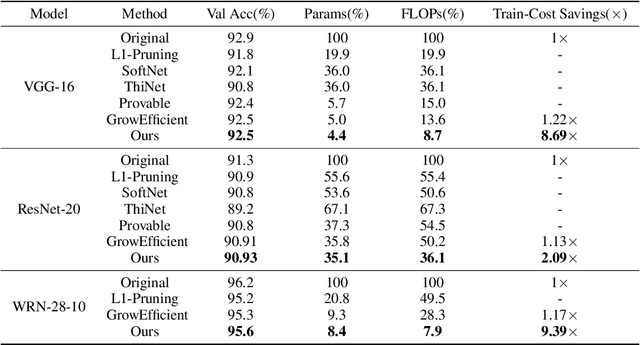
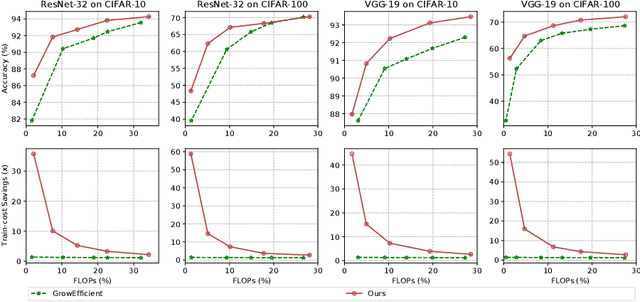
Sparse training is a natural idea to accelerate the training speed of deep neural networks and save the memory usage, especially since large modern neural networks are significantly over-parameterized. However, most of the existing methods cannot achieve this goal in practice because the chain rule based gradient (w.r.t. structure parameters) estimators adopted by previous methods require dense computation at least in the backward propagation step. This paper solves this problem by proposing an efficient sparse training method with completely sparse forward and backward passes. We first formulate the training process as a continuous minimization problem under global sparsity constraint. We then separate the optimization process into two steps, corresponding to weight update and structure parameter update. For the former step, we use the conventional chain rule, which can be sparse via exploiting the sparse structure. For the latter step, instead of using the chain rule based gradient estimators as in existing methods, we propose a variance reduced policy gradient estimator, which only requires two forward passes without backward propagation, thus achieving completely sparse training. We prove that the variance of our gradient estimator is bounded. Extensive experimental results on real-world datasets demonstrate that compared to previous methods, our algorithm is much more effective in accelerating the training process, up to an order of magnitude faster.