Efficient Neural Network Training via Forward and Backward Propagation Sparsification
Paper and Code
Nov 10, 2021

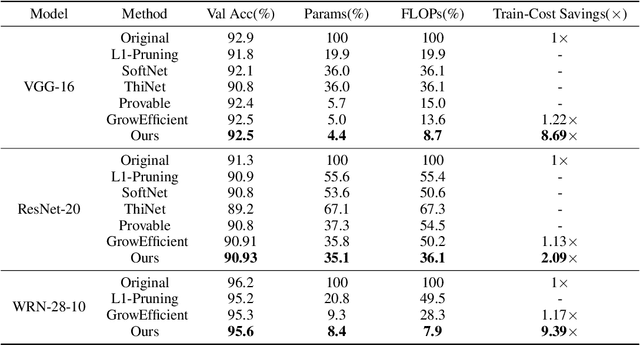
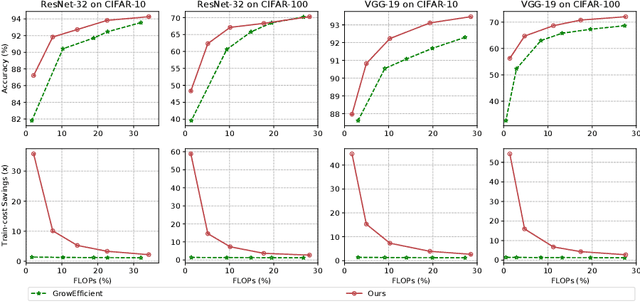
Sparse training is a natural idea to accelerate the training speed of deep neural networks and save the memory usage, especially since large modern neural networks are significantly over-parameterized. However, most of the existing methods cannot achieve this goal in practice because the chain rule based gradient (w.r.t. structure parameters) estimators adopted by previous methods require dense computation at least in the backward propagation step. This paper solves this problem by proposing an efficient sparse training method with completely sparse forward and backward passes. We first formulate the training process as a continuous minimization problem under global sparsity constraint. We then separate the optimization process into two steps, corresponding to weight update and structure parameter update. For the former step, we use the conventional chain rule, which can be sparse via exploiting the sparse structure. For the latter step, instead of using the chain rule based gradient estimators as in existing methods, we propose a variance reduced policy gradient estimator, which only requires two forward passes without backward propagation, thus achieving completely sparse training. We prove that the variance of our gradient estimator is bounded. Extensive experimental results on real-world datasets demonstrate that compared to previous methods, our algorithm is much more effective in accelerating the training process, up to an order of magnitude faster.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge