Mauricio Álvarez
Multi-task Causal Learning with Gaussian Processes
Sep 27, 2020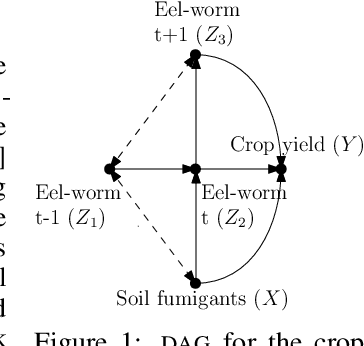
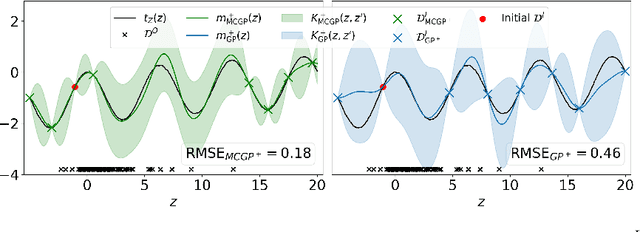
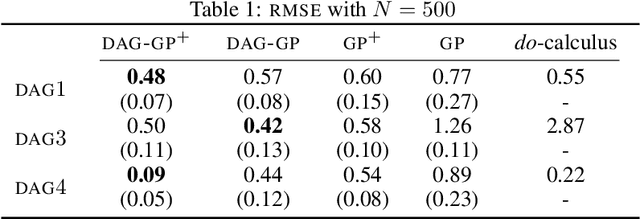
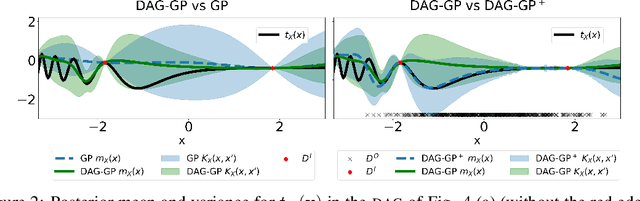
Abstract:This paper studies the problem of learning the correlation structure of a set of intervention functions defined on the directed acyclic graph (DAG) of a causal model. This is useful when we are interested in jointly learning the causal effects of interventions on different subsets of variables in a DAG, which is common in field such as healthcare or operations research. We propose the first multi-task causal Gaussian process (GP) model, which we call DAG-GP, that allows for information sharing across continuous interventions and across experiments on different variables. DAG-GP accommodates different assumptions in terms of data availability and captures the correlation between functions lying in input spaces of different dimensionality via a well-defined integral operator. We give theoretical results detailing when and how the DAG-GP model can be formulated depending on the DAG. We test both the quality of its predictions and its calibrated uncertainties. Compared to single-task models, DAG-GP achieves the best fitting performance in a variety of real and synthetic settings. In addition, it helps to select optimal interventions faster than competing approaches when used within sequential decision making frameworks, like active learning or Bayesian optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge