Decision Making under Model Misspecification: DRO with Robust Bayesian Ambiguity Sets

Distributionally Robust Optimisation (DRO) protects risk-averse decision-makers by considering the worst-case risk within an ambiguity set of distributions based on the empirical distribution or a model. To further guard against finite, noisy data, model-based approaches admit Bayesian formulations that propagate uncertainty from the posterior to the decision-making problem. However, when the model is misspecified, the decision maker must stretch the ambiguity set to contain the data-generating process (DGP), leading to overly conservative decisions. We address this challenge by introducing DRO with Robust, to model misspecification, Bayesian Ambiguity Sets (DRO-RoBAS). These are Maximum Mean Discrepancy ambiguity sets centred at a robust posterior predictive distribution that incorporates beliefs about the DGP. We show that the resulting optimisation problem obtains a dual formulation in the Reproducing Kernel Hilbert Space and we give probabilistic guarantees on the tolerance level of the ambiguity set. Our method outperforms other Bayesian and empirical DRO approaches in out-of-sample performance on the Newsvendor and Portfolio problems with various cases of model misspecification.

Federated Generalised Variational Inference: A Robust Probabilistic Federated Learning Framework

We introduce FedGVI, a probabilistic Federated Learning (FL) framework that is provably robust to both prior and likelihood misspecification. FedGVI addresses limitations in both frequentist and Bayesian FL by providing unbiased predictions under model misspecification, with calibrated uncertainty quantification. Our approach generalises previous FL approaches, specifically Partitioned Variational Inference (Ashman et al., 2022), by allowing robust and conjugate updates, decreasing computational complexity at the clients. We offer theoretical analysis in terms of fixed-point convergence, optimality of the cavity distribution, and provable robustness. Additionally, we empirically demonstrate the effectiveness of FedGVI in terms of improved robustness and predictive performance on multiple synthetic and real world classification data sets.

Decision Making under the Exponential Family: Distributionally Robust Optimisation with Bayesian Ambiguity Sets

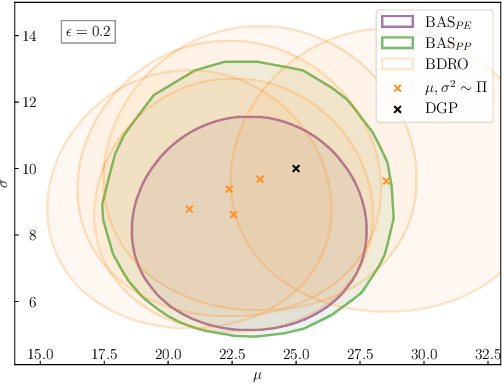
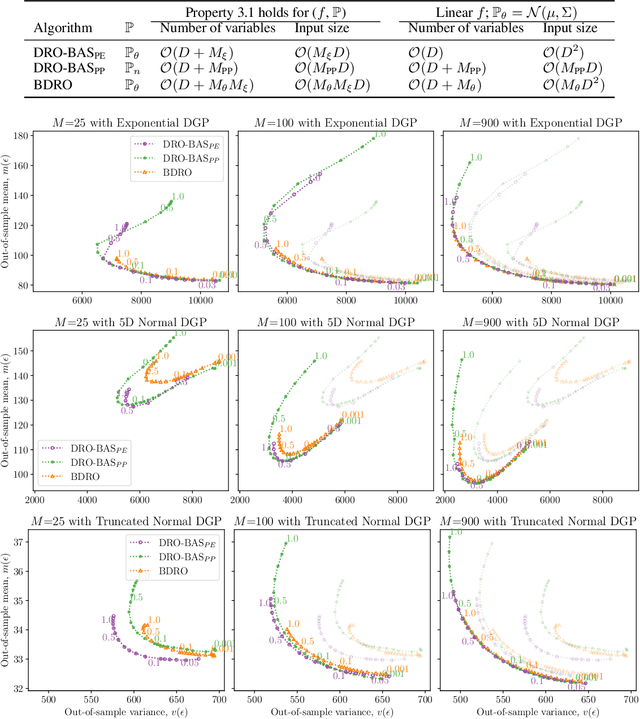
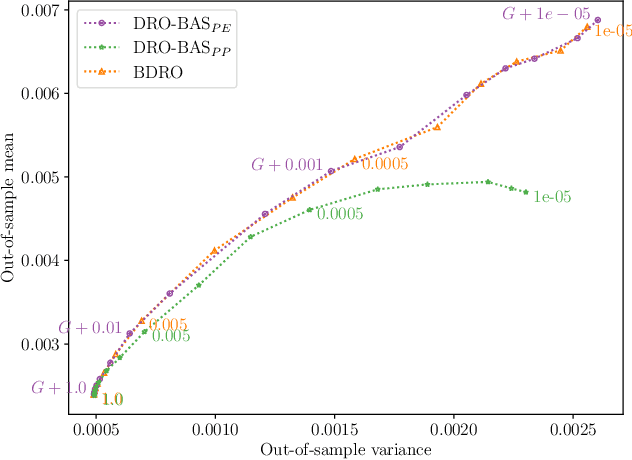
Decision making under uncertainty is challenging as the data-generating process (DGP) is often unknown. Bayesian inference proceeds by estimating the DGP through posterior beliefs on the model's parameters. However, minimising the expected risk under these beliefs can lead to suboptimal decisions due to model uncertainty or limited, noisy observations. To address this, we introduce Distributionally Robust Optimisation with Bayesian Ambiguity Sets (DRO-BAS) which hedges against model uncertainty by optimising the worst-case risk over a posterior-informed ambiguity set. We provide two such sets, based on posterior expectations (DRO-BAS(PE)) or posterior predictives (DRO-BAS(PP)) and prove that both admit, under conditions, strong dual formulations leading to efficient single-stage stochastic programs which are solved with a sample average approximation. For DRO-BAS(PE) this covers all conjugate exponential family members while for DRO-BAS(PP) this is shown under conditions on the predictive's moment generating function. Our DRO-BAS formulations Pareto dominate existing Bayesian DRO on the Newsvendor problem and achieve faster solve times with comparable robustness on the Portfolio problem.

Generating Origin-Destination Matrices in Neural Spatial Interaction Models

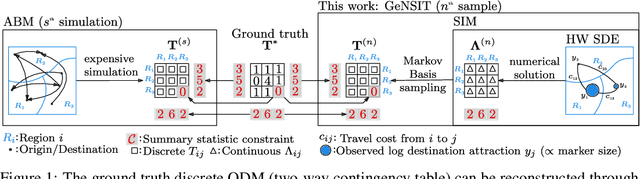
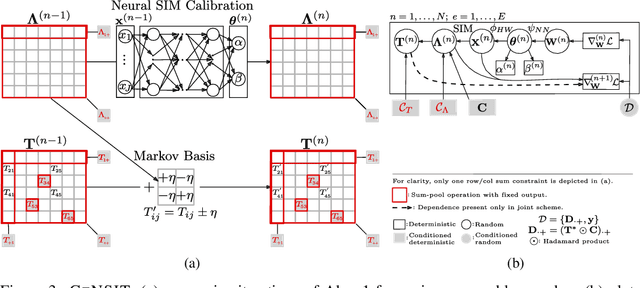
Agent-based models (ABMs) are proliferating as decision-making tools across policy areas in transportation, economics, and epidemiology. In these models, a central object of interest is the discrete origin-destination matrix which captures spatial interactions and agent trip counts between locations. Existing approaches resort to continuous approximations of this matrix and subsequent ad-hoc discretisations in order to perform ABM simulation and calibration. This impedes conditioning on partially observed summary statistics, fails to explore the multimodal matrix distribution over a discrete combinatorial support, and incurs discretisation errors. To address these challenges, we introduce a computationally efficient framework that scales linearly with the number of origin-destination pairs, operates directly on the discrete combinatorial space, and learns the agents' trip intensity through a neural differential equation that embeds spatial interactions. Our approach outperforms the prior art in terms of reconstruction error and ground truth matrix coverage, at a fraction of the computational cost. We demonstrate these benefits in large-scale spatial mobility ABMs in Cambridge, UK and Washington, DC, USA.

Physics-Informed Variational State-Space Gaussian Processes

Differential equations are important mechanistic models that are integral to many scientific and engineering applications. With the abundance of available data there has been a growing interest in data-driven physics-informed models. Gaussian processes (GPs) are particularly suited to this task as they can model complex, non-linear phenomena whilst incorporating prior knowledge and quantifying uncertainty. Current approaches have found some success but are limited as they either achieve poor computational scalings or focus only on the temporal setting. This work addresses these issues by introducing a variational spatio-temporal state-space GP that handles linear and non-linear physical constraints while achieving efficient linear-in-time computation costs. We demonstrate our methods in a range of synthetic and real-world settings and outperform the current state-of-the-art in both predictive and computational performance.

Distributionally Robust Optimisation with Bayesian Ambiguity Sets

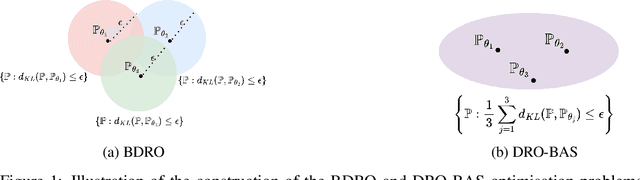
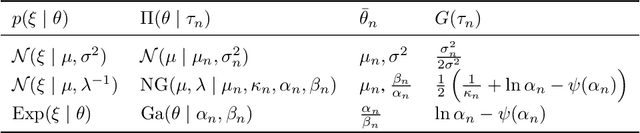
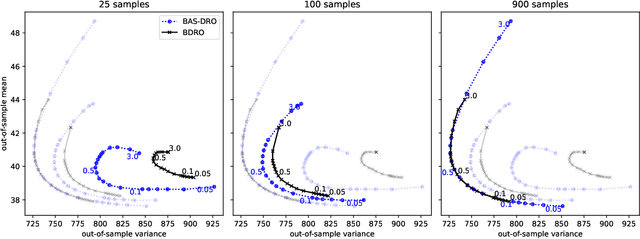
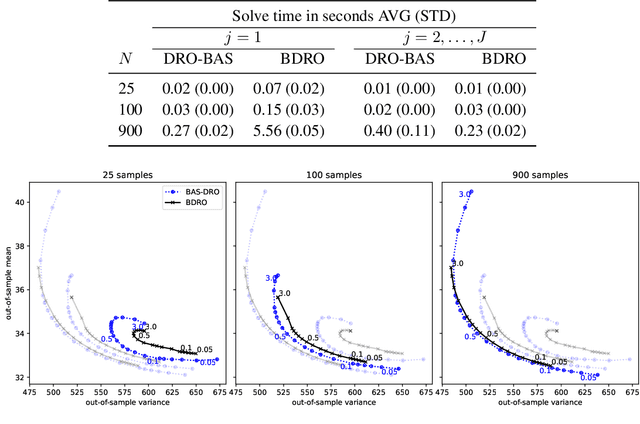
Decision making under uncertainty is challenging since the data-generating process (DGP) is often unknown. Bayesian inference proceeds by estimating the DGP through posterior beliefs about the model's parameters. However, minimising the expected risk under these posterior beliefs can lead to sub-optimal decisions due to model uncertainty or limited, noisy observations. To address this, we introduce Distributionally Robust Optimisation with Bayesian Ambiguity Sets (DRO-BAS) which hedges against uncertainty in the model by optimising the worst-case risk over a posterior-informed ambiguity set. We show that our method admits a closed-form dual representation for many exponential family members and showcase its improved out-of-sample robustness against existing Bayesian DRO methodology in the Newsvendor problem.

Causally Abstracted Multi-armed Bandits

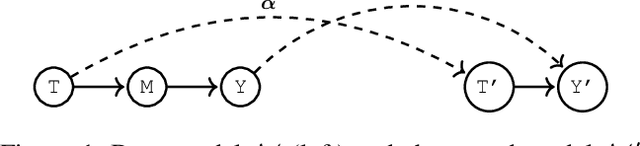
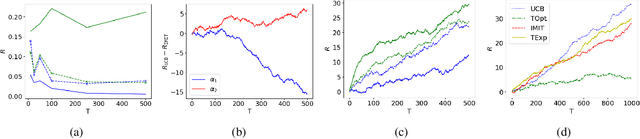
Multi-armed bandits (MAB) and causal MABs (CMAB) are established frameworks for decision-making problems. The majority of prior work typically studies and solves individual MAB and CMAB in isolation for a given problem and associated data. However, decision-makers are often faced with multiple related problems and multi-scale observations where joint formulations are needed in order to efficiently exploit the problem structures and data dependencies. Transfer learning for CMABs addresses the situation where models are defined on identical variables, although causal connections may differ. In this work, we extend transfer learning to setups involving CMABs defined on potentially different variables, with varying degrees of granularity, and related via an abstraction map. Formally, we introduce the problem of causally abstracted MABs (CAMABs) by relying on the theory of causal abstraction in order to express a rigorous abstraction map. We propose algorithms to learn in a CAMAB, and study their regret. We illustrate the limitations and the strengths of our algorithms on a real-world scenario related to online advertising.

Interventionally Consistent Surrogates for Agent-based Simulators

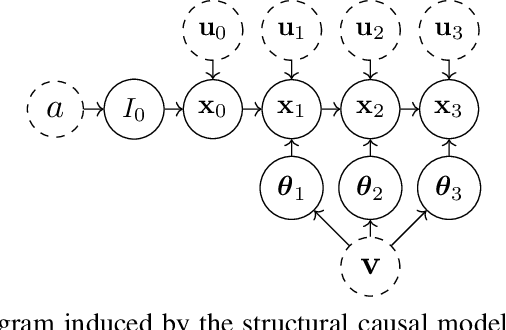
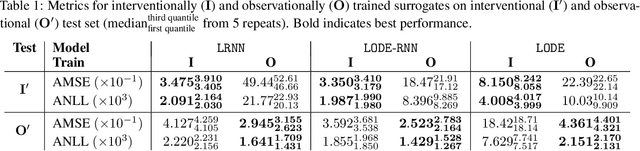
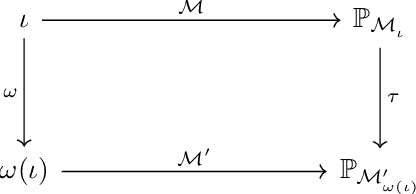
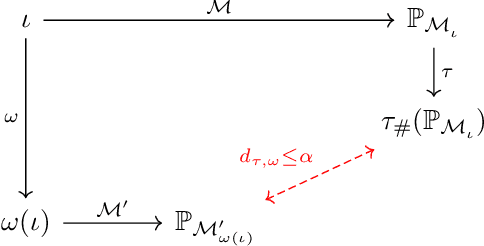
Agent-based simulators provide granular representations of complex intelligent systems by directly modelling the interactions of the system's constituent agents. Their high-fidelity nature enables hyper-local policy evaluation and testing of what-if scenarios, but is associated with large computational costs that inhibits their widespread use. Surrogate models can address these computational limitations, but they must behave consistently with the agent-based model under policy interventions of interest. In this paper, we capitalise on recent developments on causal abstractions to develop a framework for learning interventionally consistent surrogate models for agent-based simulators. Our proposed approach facilitates rapid experimentation with policy interventions in complex systems, while inducing surrogates to behave consistently with high probability with respect to the agent-based simulator across interventions of interest. We demonstrate with empirical studies that observationally trained surrogates can misjudge the effect of interventions and misguide policymakers towards suboptimal policies, while surrogates trained for interventional consistency with our proposed method closely mimic the behaviour of an agent-based model under interventions of interest.

Causal Optimal Transport of Abstractions

Causal abstraction (CA) theory establishes formal criteria for relating multiple structural causal models (SCMs) at different levels of granularity by defining maps between them. These maps have significant relevance for real-world challenges such as synthesizing causal evidence from multiple experimental environments, learning causally consistent representations at different resolutions, and linking interventions across multiple SCMs. In this work, we propose COTA, the first method to learn abstraction maps from observational and interventional data without assuming complete knowledge of the underlying SCMs. In particular, we introduce a multi-marginal Optimal Transport (OT) formulation that enforces do-calculus causal constraints, together with a cost function that relies on interventional information. We extensively evaluate COTA on synthetic and real world problems, and showcase its advantages over non-causal, independent and aggregated COTA formulations. Finally, we demonstrate the efficiency of our method as a data augmentation tool by comparing it against the state-of-the-art CA learning framework, which assumes fully specified SCMs, on a real-world downstream task.

Robust Bayesian Inference for Measurement Error Models

Measurement error occurs when a set of covariates influencing a response variable are corrupted by noise. This can lead to misleading inference outcomes, particularly in problems where accurately estimating the relationship between covariates and response variables is crucial, such as causal effect estimation. Existing methods for dealing with measurement error often rely on strong assumptions such as knowledge of the error distribution or its variance and availability of replicated measurements of the covariates. We propose a Bayesian Nonparametric Learning framework which is robust to mismeasured covariates, does not require the preceding assumptions, and is able to incorporate prior beliefs about the true error distribution. Our approach gives rise to two methods that are robust to measurement error via different loss functions: one based on the Total Least Squares objective and the other based on Maximum Mean Discrepancy (MMD). The latter allows for generalisation to non-Gaussian distributed errors and non-linear covariate-response relationships. We provide bounds on the generalisation error using the MMD-loss and showcase the effectiveness of the proposed framework versus prior art in real-world mental health and dietary datasets that contain significant measurement errors.