Guarantees of a Preconditioned Subgradient Algorithm for Overparameterized Asymmetric Low-rank Matrix Recovery

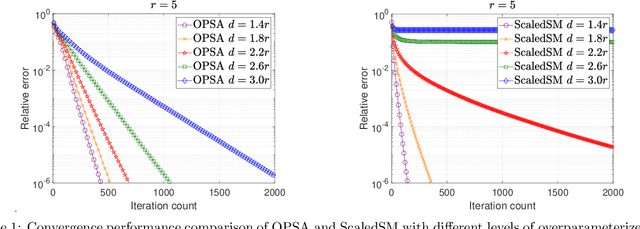
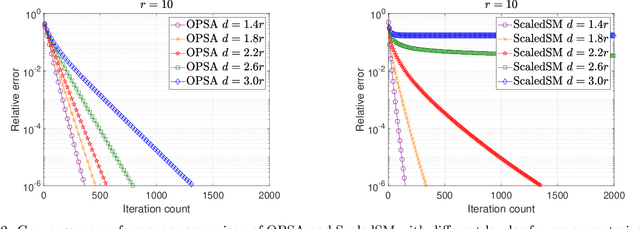
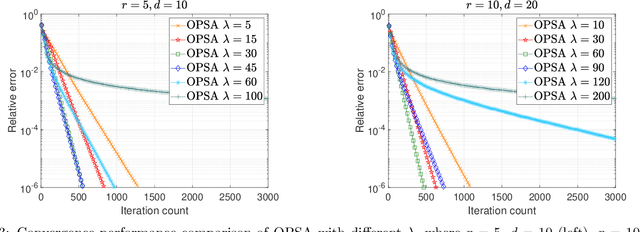
In this paper, we focus on a matrix factorization-based approach for robust low-rank and asymmetric matrix recovery from corrupted measurements. We address the challenging scenario where the rank of the sought matrix is unknown and employ an overparameterized approach using the variational form of the nuclear norm as a regularizer. We propose a subgradient algorithm that inherits the merits of preconditioned algorithms, whose rate of convergence does not depend on the condition number of the sought matrix, and addresses their current limitation, i.e., the lack of convergence guarantees in the case of asymmetric matrices with unknown rank. In this setting, we provide, for the first time in the literature, linear convergence guarantees for the derived overparameterized preconditioned subgradient algorithm in the presence of gross corruptions. Additionally, by applying our approach to matrix sensing, we highlight its merits when the measurement operator satisfies the mixed-norm restricted isometry properties. Lastly, we present numerical experiments that validate our theoretical results and demonstrate the effectiveness of our approach.

Clustering-based Domain-Incremental Learning

We consider the problem of learning multiple tasks in a continual learning setting in which data from different tasks is presented to the learner in a streaming fashion. A key challenge in this setting is the so-called "catastrophic forgetting problem", in which the performance of the learner in an "old task" decreases when subsequently trained on a "new task". Existing continual learning methods, such as Averaged Gradient Episodic Memory (A-GEM) and Orthogonal Gradient Descent (OGD), address catastrophic forgetting by minimizing the loss for the current task without increasing the loss for previous tasks. However, these methods assume the learner knows when the task changes, which is unrealistic in practice. In this paper, we alleviate the need to provide the algorithm with information about task changes by using an online clustering-based approach on a dynamically updated finite pool of samples or gradients. We thereby successfully counteract catastrophic forgetting in one of the hardest settings, namely: domain-incremental learning, a setting for which the problem was previously unsolved. We showcase the benefits of our approach by applying these ideas to projection-based methods, such as A-GEM and OGD, which lead to task-agnostic versions of them. Experiments on real datasets demonstrate the effectiveness of the proposed strategy and its promising performance compared to state-of-the-art methods.

A Linearly Convergent GAN Inversion-based Algorithm for Reverse Engineering of Deceptions

An important aspect of developing reliable deep learning systems is devising strategies that make these systems robust to adversarial attacks. There is a long line of work that focuses on developing defenses against these attacks, but recently, researchers have began to study ways to reverse engineer the attack process. This allows us to not only defend against several attack models, but also classify the threat model. However, there is still a lack of theoretical guarantees for the reverse engineering process. Current approaches that give any guarantees are based on the assumption that the data lies in a union of linear subspaces, which is not a valid assumption for more complex datasets. In this paper, we build on prior work and propose a novel framework for reverse engineering of deceptions which supposes that the clean data lies in the range of a GAN. To classify the signal and attack, we jointly solve a GAN inversion problem and a block-sparse recovery problem. For the first time in the literature, we provide deterministic linear convergence guarantees for this problem. We also empirically demonstrate the merits of the proposed approach on several nonlinear datasets as compared to state-of-the-art methods.

Reverse Engineering $\ell_p$ attacks: A block-sparse optimization approach with recovery guarantees

Deep neural network-based classifiers have been shown to be vulnerable to imperceptible perturbations to their input, such as $\ell_p$-bounded norm adversarial attacks. This has motivated the development of many defense methods, which are then broken by new attacks, and so on. This paper focuses on a different but related problem of reverse engineering adversarial attacks. Specifically, given an attacked signal, we study conditions under which one can determine the type of attack ($\ell_1$, $\ell_2$ or $\ell_\infty$) and recover the clean signal. We pose this problem as a block-sparse recovery problem, where both the signal and the attack are assumed to lie in a union of subspaces that includes one subspace per class and one subspace per attack type. We derive geometric conditions on the subspaces under which any attacked signal can be decomposed as the sum of a clean signal plus an attack. In addition, by determining the subspaces that contain the signal and the attack, we can also classify the signal and determine the attack type. Experiments on digit and face classification demonstrate the effectiveness of the proposed approach.

Simultaneously sparse and low-rank abundance matrix estimation for hyperspectral image unmixing

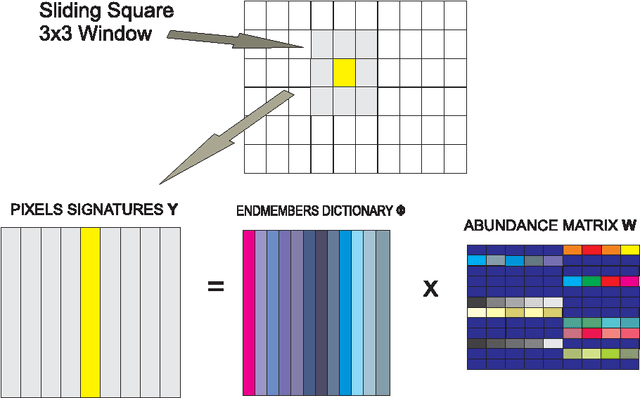
In a plethora of applications dealing with inverse problems, e.g. in image processing, social networks, compressive sensing, biological data processing etc., the signal of interest is known to be structured in several ways at the same time. This premise has recently guided the research to the innovative and meaningful idea of imposing multiple constraints on the parameters involved in the problem under study. For instance, when dealing with problems whose parameters form sparse and low-rank matrices, the adoption of suitably combined constraints imposing sparsity and low-rankness, is expected to yield substantially enhanced estimation results. In this paper, we address the spectral unmixing problem in hyperspectral images. Specifically, two novel unmixing algorithms are introduced, in an attempt to exploit both spatial correlation and sparse representation of pixels lying in homogeneous regions of hyperspectral images. To this end, a novel convex mixed penalty term is first defined consisting of the sum of the weighted $\ell_1$ and the weighted nuclear norm of the abundance matrix corresponding to a small area of the image determined by a sliding square window. This penalty term is then used to regularize a conventional quadratic cost function and impose simultaneously sparsity and row-rankness on the abundance matrix. The resulting regularized cost function is minimized by a) an incremental proximal sparse and low-rank unmixing algorithm and b) an algorithm based on the alternating minimization method of multipliers (ADMM). The effectiveness of the proposed algorithms is illustrated in experiments conducted both on simulated and real data.