Physics-Informed Variational State-Space Gaussian Processes

Differential equations are important mechanistic models that are integral to many scientific and engineering applications. With the abundance of available data there has been a growing interest in data-driven physics-informed models. Gaussian processes (GPs) are particularly suited to this task as they can model complex, non-linear phenomena whilst incorporating prior knowledge and quantifying uncertainty. Current approaches have found some success but are limited as they either achieve poor computational scalings or focus only on the temporal setting. This work addresses these issues by introducing a variational spatio-temporal state-space GP that handles linear and non-linear physical constraints while achieving efficient linear-in-time computation costs. We demonstrate our methods in a range of synthetic and real-world settings and outperform the current state-of-the-art in both predictive and computational performance.

Spatio-Temporal Variational Gaussian Processes

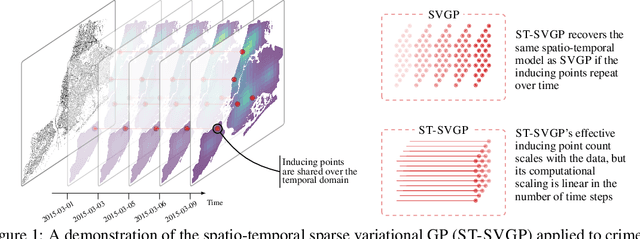
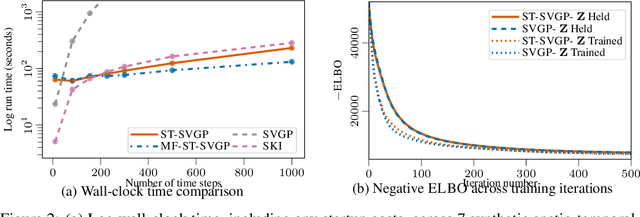
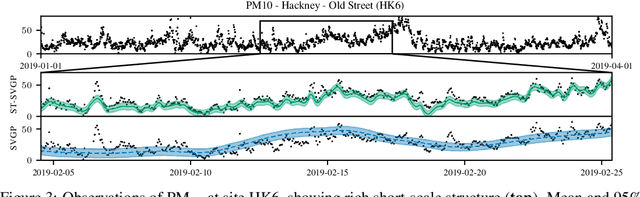
We introduce a scalable approach to Gaussian process inference that combines spatio-temporal filtering with natural gradient variational inference, resulting in a non-conjugate GP method for multivariate data that scales linearly with respect to time. Our natural gradient approach enables application of parallel filtering and smoothing, further reducing the temporal span complexity to be logarithmic in the number of time steps. We derive a sparse approximation that constructs a state-space model over a reduced set of spatial inducing points, and show that for separable Markov kernels the full and sparse cases exactly recover the standard variational GP, whilst exhibiting favourable computational properties. To further improve the spatial scaling we propose a mean-field assumption of independence between spatial locations which, when coupled with sparsity and parallelisation, leads to an efficient and accurate method for large spatio-temporal problems.

Transforming Gaussian Processes With Normalizing Flows

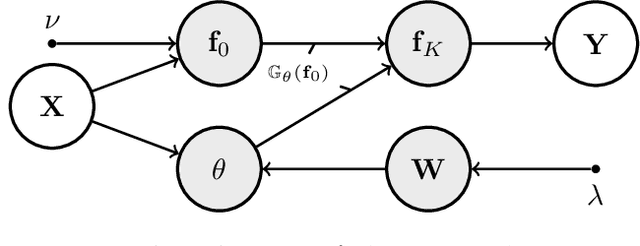
Gaussian Processes (GPs) can be used as flexible, non-parametric function priors. Inspired by the growing body of work on Normalizing Flows, we enlarge this class of priors through a parametric invertible transformation that can be made input-dependent. Doing so also allows us to encode interpretable prior knowledge (e.g., boundedness constraints). We derive a variational approximation to the resulting Bayesian inference problem, which is as fast as stochastic variational GP regression (Hensman et al., 2013; Dezfouli and Bonilla,2015). This makes the model a computationally efficient alternative to other hierarchical extensions of GP priors (Lazaro-Gredilla,2012; Damianou and Lawrence, 2013). The resulting algorithm's computational and inferential performance is excellent, and we demonstrate this on a range of data sets. For example, even with only 5 inducing points and an input-dependent flow, our method is consistently competitive with a standard sparse GP fitted using 100 inducing points.

Multi-resolution Multi-task Gaussian Processes

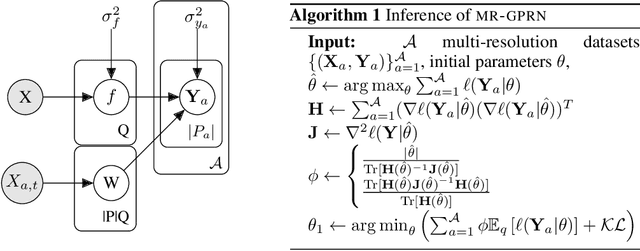
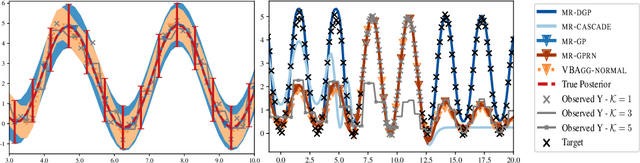
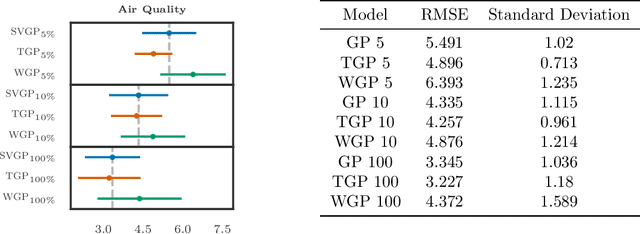
We consider evidence integration from potentially dependent observation processes under varying spatio-temporal sampling resolutions and noise levels. We develop a multi-resolution multi-task (MRGP) framework while allowing for both inter-task and intra-task multi-resolution and multi-fidelity. We develop shallow Gaussian Process (GP) mixtures that approximate the difficult to estimate joint likelihood with a composite one and deep GP constructions that naturally handle biases in the mean. By doing so, we generalize and outperform state of the art GP compositions and offer information-theoretic corrections and efficient variational approximations. We demonstrate the competitiveness of MRGPs on synthetic settings and on the challenging problem of hyper-local estimation of air pollution levels across London from multiple sensing modalities operating at disparate spatio-temporal resolutions.