Jeremias Knoblauch
Robust Bayesian Optimisation with Unbounded Corruptions
Nov 19, 2025Abstract:Bayesian Optimization is critically vulnerable to extreme outliers. Existing provably robust methods typically assume a bounded cumulative corruption budget, which makes them defenseless against even a single corruption of sufficient magnitude. To address this, we introduce a new adversary whose budget is only bounded in the frequency of corruptions, not in their magnitude. We then derive RCGP-UCB, an algorithm coupling the famous upper confidence bound (UCB) approach with a Robust Conjugate Gaussian Process (RCGP). We present stable and adaptive versions of RCGP-UCB, and prove that they achieve sublinear regret in the presence of up to $O(T^{1/2})$ and $O(T^{1/3})$ corruptions with possibly infinite magnitude. This robustness comes at near zero cost: without outliers, RCGP-UCB's regret bounds match those of the standard GP-UCB algorithm.
Multi-Output Robust and Conjugate Gaussian Processes
Oct 30, 2025Abstract:Multi-output Gaussian process (MOGP) regression allows modelling dependencies among multiple correlated response variables. Similarly to standard Gaussian processes, MOGPs are sensitive to model misspecification and outliers, which can distort predictions within individual outputs. This situation can be further exacerbated by multiple anomalous response variables whose errors propagate due to correlations between outputs. To handle this situation, we extend and generalise the robust and conjugate Gaussian process (RCGP) framework introduced by Altamirano et al. (2024). This results in the multi-output RCGP (MO-RCGP): a provably robust MOGP that is conjugate, and jointly captures correlations across outputs. We thoroughly evaluate our approach through applications in finance and cancer research.
Predictively Oriented Posteriors
Oct 02, 2025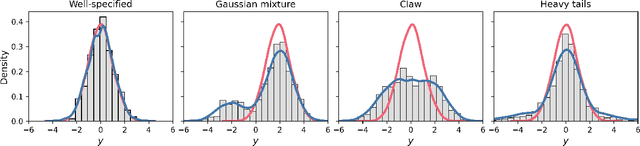
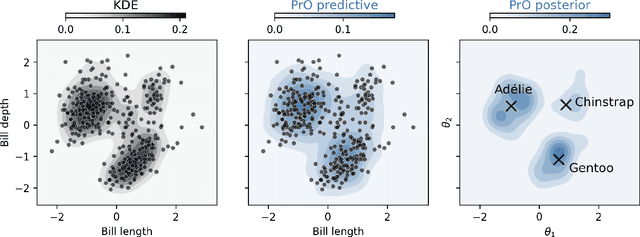
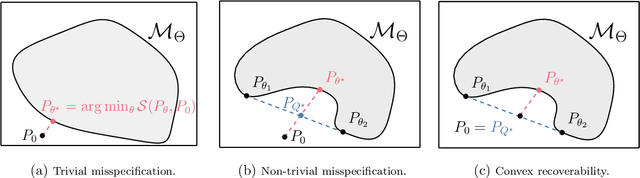
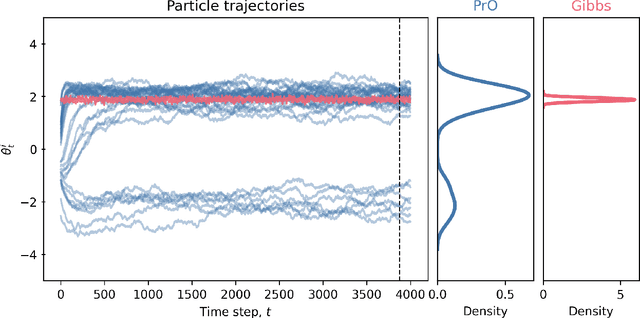
Abstract:We advocate for a new statistical principle that combines the most desirable aspects of both parameter inference and density estimation. This leads us to the predictively oriented (PrO) posterior, which expresses uncertainty as a consequence of predictive ability. Doing so leads to inferences which predictively dominate both classical and generalised Bayes posterior predictive distributions: up to logarithmic factors, PrO posteriors converge to the predictively optimal model average at rate $n^{-1/2}$. Whereas classical and generalised Bayes posteriors only achieve this rate if the model can recover the data-generating process, PrO posteriors adapt to the level of model misspecification. This means that they concentrate around the true model at rate $n^{1/2}$ in the same way as Bayes and Gibbs posteriors if the model can recover the data-generating distribution, but do \textit{not} concentrate in the presence of non-trivial forms of model misspecification. Instead, they stabilise towards a predictively optimal posterior whose degree of irreducible uncertainty admits an interpretation as the degree of model misspecification -- a sharp contrast to how Bayesian uncertainty and its existing extensions behave. Lastly, we show that PrO posteriors can be sampled from by evolving particles based on mean field Langevin dynamics, and verify the practical significance of our theoretical developments on a number of numerical examples.
Near-Optimal Approximations for Bayesian Inference in Function Space
Feb 25, 2025Abstract:We propose a scalable inference algorithm for Bayes posteriors defined on a reproducing kernel Hilbert space (RKHS). Given a likelihood function and a Gaussian random element representing the prior, the corresponding Bayes posterior measure $\Pi_{\text{B}}$ can be obtained as the stationary distribution of an RKHS-valued Langevin diffusion. We approximate the infinite-dimensional Langevin diffusion via a projection onto the first $M$ components of the Kosambi-Karhunen-Lo\`eve expansion. Exploiting the thus obtained approximate posterior for these $M$ components, we perform inference for $\Pi_{\text{B}}$ by relying on the law of total probability and a sufficiency assumption. The resulting method scales as $O(M^3+JM^2)$, where $J$ is the number of samples produced from the posterior measure $\Pi_{\text{B}}$. Interestingly, the algorithm recovers the posterior arising from the sparse variational Gaussian process (SVGP) (see Titsias, 2009) as a special case, owed to the fact that the sufficiency assumption underlies both methods. However, whereas the SVGP is parametrically constrained to be a Gaussian process, our method is based on a non-parametric variational family $\mathcal{P}(\mathbb{R}^M)$ consisting of all probability measures on $\mathbb{R}^M$. As a result, our method is provably close to the optimal $M$-dimensional variational approximation of the Bayes posterior $\Pi_{\text{B}}$ in $\mathcal{P}(\mathbb{R}^M)$ for convex and Lipschitz continuous negative log likelihoods, and coincides with SVGP for the special case of a Gaussian error likelihood.
Robust and Conjugate Spatio-Temporal Gaussian Processes
Feb 04, 2025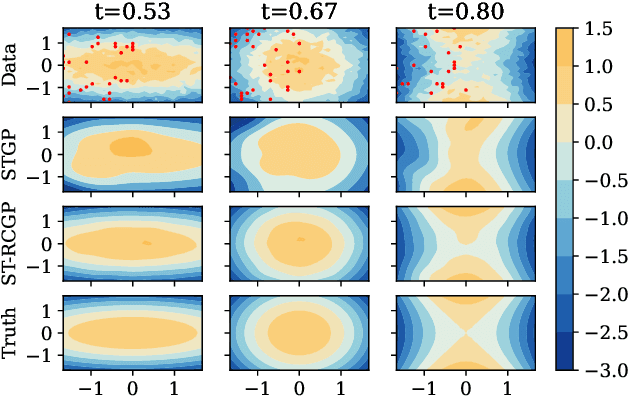
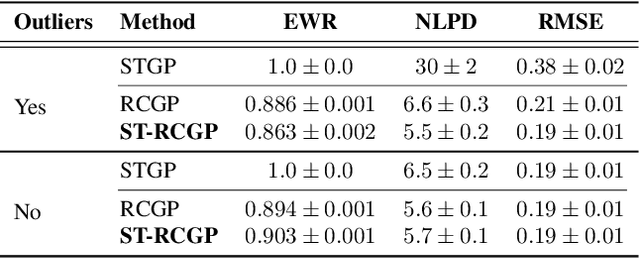
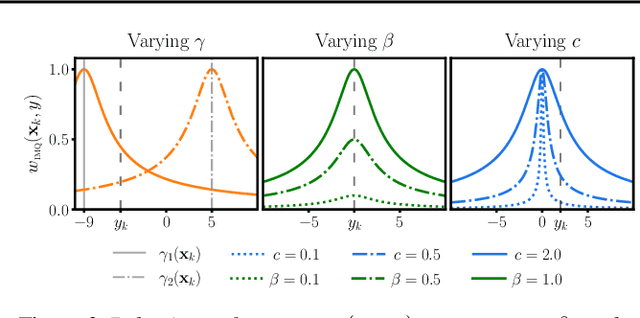
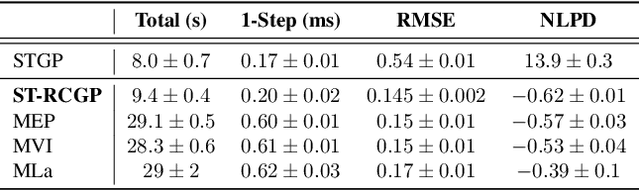
Abstract:State-space formulations allow for Gaussian process (GP) regression with linear-in-time computational cost in spatio-temporal settings, but performance typically suffers in the presence of outliers. In this paper, we adapt and specialise the robust and conjugate GP (RCGP) framework of Altamirano et al. (2024) to the spatio-temporal setting. In doing so, we obtain an outlier-robust spatio-temporal GP with a computational cost comparable to classical spatio-temporal GPs. We also overcome the three main drawbacks of RCGPs: their unreliable performance when the prior mean is chosen poorly, their lack of reliable uncertainty quantification, and the need to carefully select a hyperparameter by hand. We study our method extensively in finance and weather forecasting applications, demonstrating that it provides a reliable approach to spatio-temporal modelling in the presence of outliers.
Outlier-robust Kalman Filtering through Generalised Bayes
May 09, 2024Abstract:We derive a novel, provably robust, and closed-form Bayesian update rule for online filtering in state-space models in the presence of outliers and misspecified measurement models. Our method combines generalised Bayesian inference with filtering methods such as the extended and ensemble Kalman filter. We use the former to show robustness and the latter to ensure computational efficiency in the case of nonlinear models. Our method matches or outperforms other robust filtering methods (such as those based on variational Bayes) at a much lower computational cost. We show this empirically on a range of filtering problems with outlier measurements, such as object tracking, state estimation in high-dimensional chaotic systems, and online learning of neural networks.
Robust and Conjugate Gaussian Process Regression
Nov 01, 2023Abstract:To enable closed form conditioning, a common assumption in Gaussian process (GP) regression is independent and identically distributed Gaussian observation noise. This strong and simplistic assumption is often violated in practice, which leads to unreliable inferences and uncertainty quantification. Unfortunately, existing methods for robustifying GPs break closed-form conditioning, which makes them less attractive to practitioners and significantly more computationally expensive. In this paper, we demonstrate how to perform provably robust and conjugate Gaussian process (RCGP) regression at virtually no additional cost using generalised Bayesian inference. RCGP is particularly versatile as it enables exact conjugate closed form updates in all settings where standard GPs admit them. To demonstrate its strong empirical performance, we deploy RCGP for problems ranging from Bayesian optimisation to sparse variational Gaussian processes.
A Rigorous Link between Deep Ensembles and Bayesian Methods
May 24, 2023



Abstract:We establish the first mathematically rigorous link between Bayesian, variational Bayesian, and ensemble methods. A key step towards this it to reformulate the non-convex optimisation problem typically encountered in deep learning as a convex optimisation in the space of probability measures. On a technical level, our contribution amounts to studying generalised variational inference through the lense of Wasserstein gradient flows. The result is a unified theory of various seemingly disconnected approaches that are commonly used for uncertainty quantification in deep learning -- including deep ensembles and (variational) Bayesian methods. This offers a fresh perspective on the reasons behind the success of deep ensembles over procedures based on parameterised variational inference, and allows the derivation of new ensembling schemes with convergence guarantees. We showcase this by proposing a family of interacting deep ensembles with direct parallels to the interactions of particle systems in thermodynamics, and use our theory to prove the convergence of these algorithms to a well-defined global minimiser on the space of probability measures.
Robust and Scalable Bayesian Online Changepoint Detection
Feb 09, 2023Abstract:This paper proposes an online, provably robust, and scalable Bayesian approach for changepoint detection. The resulting algorithm has key advantages over previous work: it provides provable robustness by leveraging the generalised Bayesian perspective, and also addresses the scalability issues of previous attempts. Specifically, the proposed generalised Bayesian formalism leads to conjugate posteriors whose parameters are available in closed form by leveraging diffusion score matching. The resulting algorithm is exact, can be updated through simple algebra, and is more than 10 times faster than its closest competitor.
Generalised Bayesian Inference for Discrete Intractable Likelihood
Jun 16, 2022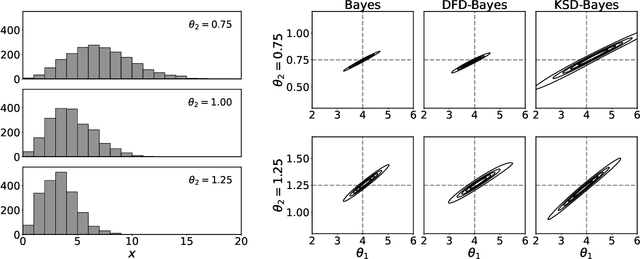
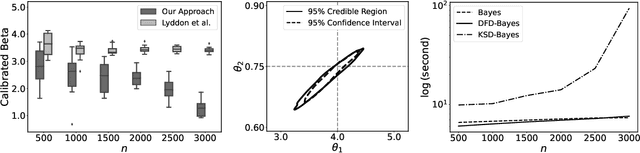
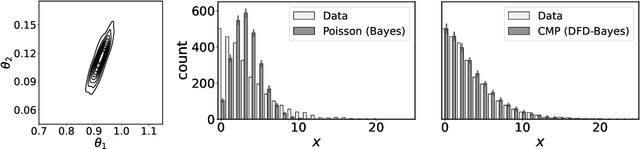
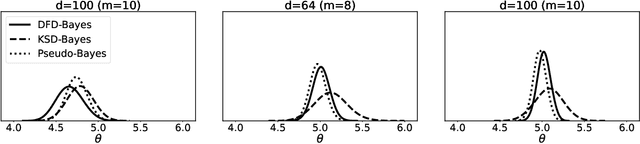
Abstract:Discrete state spaces represent a major computational challenge to statistical inference, since the computation of normalisation constants requires summation over large or possibly infinite sets, which can be impractical. This paper addresses this computational challenge through the development of a novel generalised Bayesian inference procedure suitable for discrete intractable likelihood. Inspired by recent methodological advances for continuous data, the main idea is to update beliefs about model parameters using a discrete Fisher divergence, in lieu of the problematic intractable likelihood. The result is a generalised posterior that can be sampled using standard computational tools, such as Markov chain Monte Carlo, circumventing the intractable normalising constant. The statistical properties of the generalised posterior are analysed, with sufficient conditions for posterior consistency and asymptotic normality established. In addition, a novel and general approach to calibration of generalised posteriors is proposed. Applications are presented on lattice models for discrete spatial data and on multivariate models for count data, where in each case the methodology facilitates generalised Bayesian inference at low computational cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge