OpenAI o1 System Card

The o1 model series is trained with large-scale reinforcement learning to reason using chain of thought. These advanced reasoning capabilities provide new avenues for improving the safety and robustness of our models. In particular, our models can reason about our safety policies in context when responding to potentially unsafe prompts, through deliberative alignment. This leads to state-of-the-art performance on certain benchmarks for risks such as generating illicit advice, choosing stereotyped responses, and succumbing to known jailbreaks. Training models to incorporate a chain of thought before answering has the potential to unlock substantial benefits, while also increasing potential risks that stem from heightened intelligence. Our results underscore the need for building robust alignment methods, extensively stress-testing their efficacy, and maintaining meticulous risk management protocols. This report outlines the safety work carried out for the OpenAI o1 and OpenAI o1-mini models, including safety evaluations, external red teaming, and Preparedness Framework evaluations.

Human-inspired Perspectives: A Survey on AI Long-term Memory

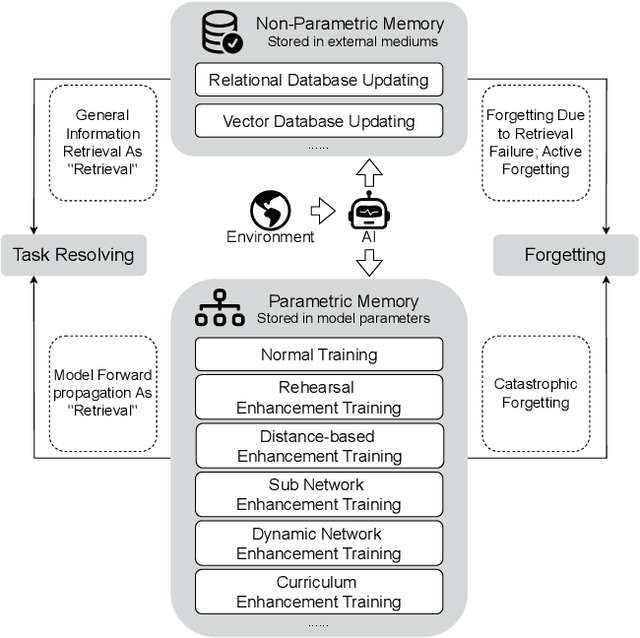
With the rapid advancement of AI systems, their abilities to store, retrieve, and utilize information over the long term - referred to as long-term memory - have become increasingly significant. These capabilities are crucial for enhancing the performance of AI systems across a wide range of tasks. However, there is currently no comprehensive survey that systematically investigates AI's long-term memory capabilities, formulates a theoretical framework, and inspires the development of next-generation AI long-term memory systems. This paper begins by systematically introducing the mechanisms of human long-term memory, then explores AI long-term memory mechanisms, establishing a mapping between the two. Based on the mapping relationships identified, we extend the current cognitive architectures and propose the Cognitive Architecture of Self-Adaptive Long-term Memory (SALM). SALM provides a theoretical framework for the practice of AI long-term memory and holds potential for guiding the creation of next-generation long-term memory driven AI systems. Finally, we delve into the future directions and application prospects of AI long-term memory.

More Experts Than Galaxies: Conditionally-overlapping Experts With Biologically-Inspired Fixed Routing

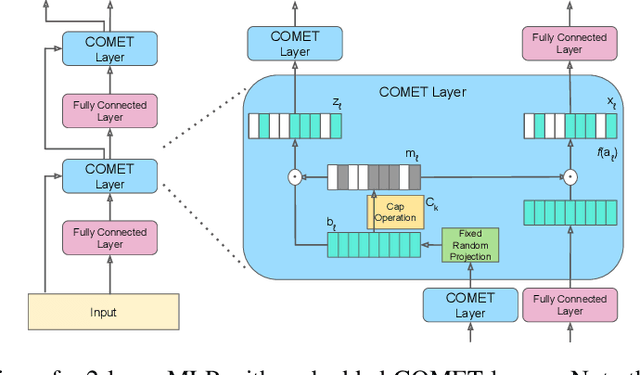
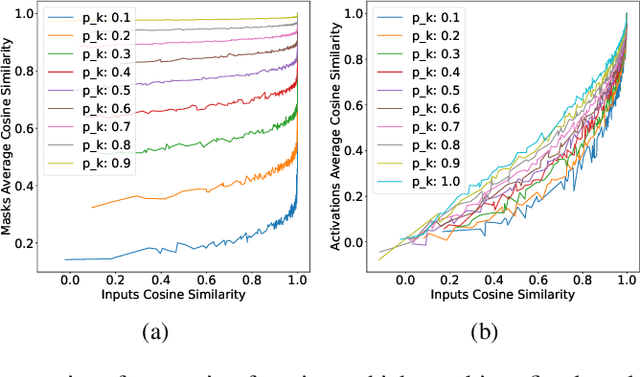
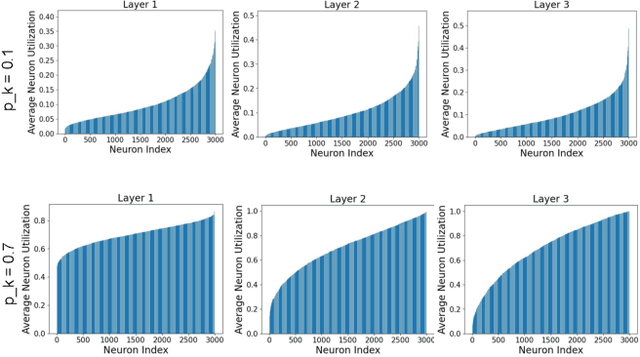
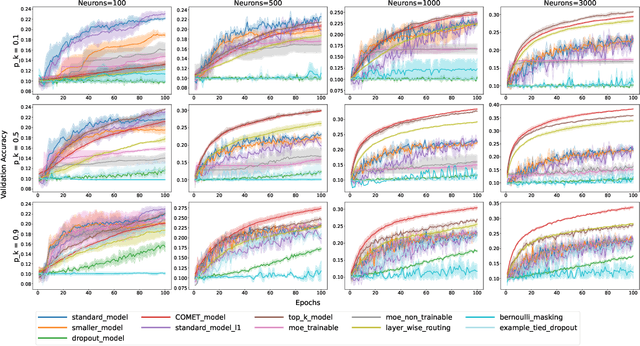
The evolution of biological neural systems has led to both modularity and sparse coding, which enables efficiency in energy usage, and robustness across the diversity of tasks in the lifespan. In contrast, standard neural networks rely on dense, non-specialized architectures, where all model parameters are simultaneously updated to learn multiple tasks, leading to representation interference. Current sparse neural network approaches aim to alleviate this issue, but are often hindered by limitations such as 1) trainable gating functions that cause representation collapse; 2) non-overlapping experts that result in redundant computation and slow learning; and 3) reliance on explicit input or task IDs that impose significant constraints on flexibility and scalability. In this paper we propose Conditionally Overlapping Mixture of ExperTs (COMET), a general deep learning method that addresses these challenges by inducing a modular, sparse architecture with an exponential number of overlapping experts. COMET replaces the trainable gating function used in Sparse Mixture of Experts with a fixed, biologically inspired random projection applied to individual input representations. This design causes the degree of expert overlap to depend on input similarity, so that similar inputs tend to share more parameters. This facilitates positive knowledge transfer, resulting in faster learning and improved generalization. We demonstrate the effectiveness of COMET on a range of tasks, including image classification, language modeling, and regression, using several popular deep learning architectures.

Bayesian Online Natural Gradient (BONG)

We propose a novel approach to sequential Bayesian inference based on variational Bayes. The key insight is that, in the online setting, we do not need to add the KL term to regularize to the prior (which comes from the posterior at the previous timestep); instead we can optimize just the expected log-likelihood, performing a single step of natural gradient descent starting at the prior predictive. We prove this method recovers exact Bayesian inference if the model is conjugate, and empirically outperforms other online VB methods in the non-conjugate setting, such as online learning for neural networks, especially when controlling for computational costs.

Outlier-robust Kalman Filtering through Generalised Bayes

We derive a novel, provably robust, and closed-form Bayesian update rule for online filtering in state-space models in the presence of outliers and misspecified measurement models. Our method combines generalised Bayesian inference with filtering methods such as the extended and ensemble Kalman filter. We use the former to show robustness and the latter to ensure computational efficiency in the case of nonlinear models. Our method matches or outperforms other robust filtering methods (such as those based on variational Bayes) at a much lower computational cost. We show this empirically on a range of filtering problems with outlier measurements, such as object tracking, state estimation in high-dimensional chaotic systems, and online learning of neural networks.

Reawakening knowledge: Anticipatory recovery from catastrophic interference via structured training

We explore the training dynamics of neural networks in a structured non-IID setting where documents are presented cyclically in a fixed, repeated sequence. Typically, networks suffer from catastrophic interference when training on a sequence of documents; however, we discover a curious and remarkable property of LLMs fine-tuned sequentially in this setting: they exhibit anticipatory behavior, recovering from the forgetting on documents before encountering them again. The behavior emerges and becomes more robust as the architecture scales up its number of parameters. Through comprehensive experiments and visualizations, we uncover new insights into training over-parameterized networks in structured environments.

Noise misleads rotation invariant algorithms on sparse targets

It is well known that the class of rotation invariant algorithms are suboptimal even for learning sparse linear problems when the number of examples is below the "dimension" of the problem. This class includes any gradient descent trained neural net with a fully-connected input layer (initialized with a rotationally symmetric distribution). The simplest sparse problem is learning a single feature out of $d$ features. In that case the classification error or regression loss grows with $1-k/n$ where $k$ is the number of examples seen. These lower bounds become vacuous when the number of examples $k$ reaches the dimension $d$. We show that when noise is added to this sparse linear problem, rotation invariant algorithms are still suboptimal after seeing $d$ or more examples. We prove this via a lower bound for the Bayes optimal algorithm on a rotationally symmetrized problem. We then prove much lower upper bounds on the same problem for simple non-rotation invariant algorithms. Finally we analyze the gradient flow trajectories of many standard optimization algorithms in some simple cases and show how they veer toward or away from the sparse targets. We believe that our trajectory categorization will be useful in designing algorithms that can exploit sparse targets and our method for proving lower bounds will be crucial for analyzing other families of algorithms that admit different classes of invariances.

Low-rank extended Kalman filtering for online learning of neural networks from streaming data

We propose an efficient online approximate Bayesian inference algorithm for estimating the parameters of a nonlinear function from a potentially non-stationary data stream. The method is based on the extended Kalman filter (EKF), but uses a novel low-rank plus diagonal decomposition of the posterior precision matrix, which gives a cost per step which is linear in the number of model parameters. In contrast to methods based on stochastic variational inference, our method is fully deterministic, and does not require step-size tuning. We show experimentally that this results in much faster (more sample efficient) learning, which results in more rapid adaptation to changing distributions, and faster accumulation of reward when used as part of a contextual bandit algorithm.

Robust priors for regularized regression

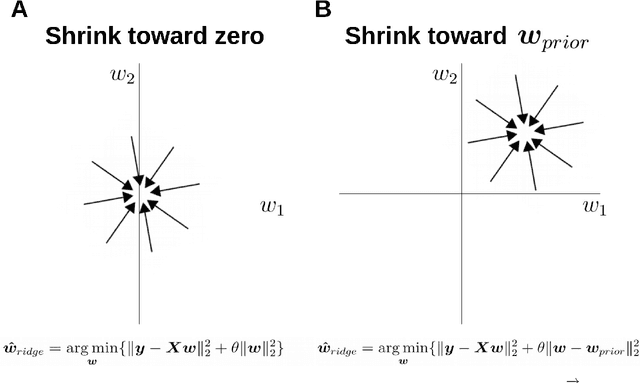
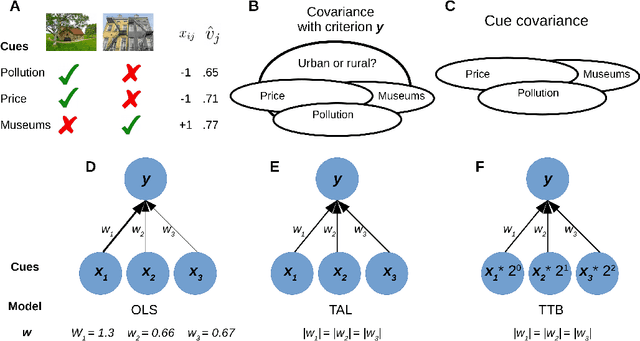
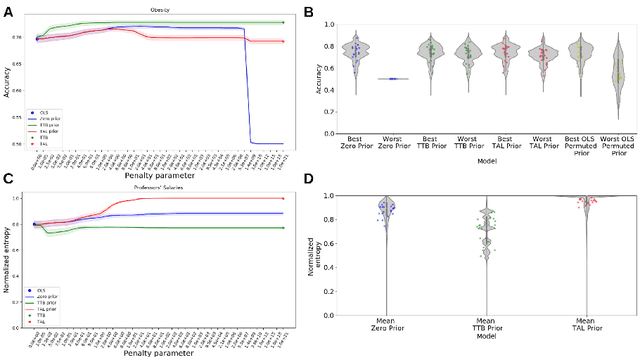
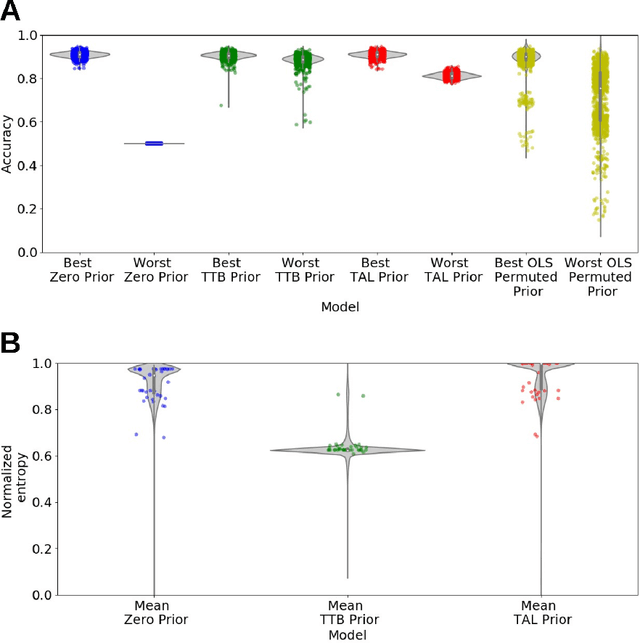
Induction benefits from useful priors. Penalized regression approaches, like ridge regression, shrink weights toward zero but zero association is usually not a sensible prior. Inspired by simple and robust decision heuristics humans use, we constructed non-zero priors for penalized regression models that provide robust and interpretable solutions across several tasks. Our approach enables estimates from a constrained model to serve as a prior for a more general model, yielding a principled way to interpolate between models of differing complexity. We successfully applied this approach to a number of decision and classification problems, as well as analyzing simulated brain imaging data. Models with robust priors had excellent worst-case performance. Solutions followed from the form of the heuristic that was used to derive the prior. These new algorithms can serve applications in data analysis and machine learning, as well as help in understanding how people transition from novice to expert performance.

Reinforcement Learning with Analogical Similarity to Guide Schema Induction and Attention

Research in analogical reasoning suggests that higher-order cognitive functions such as abstract reasoning, far transfer, and creativity are founded on recognizing structural similarities among relational systems. Here we integrate theories of analogy with the computational framework of reinforcement learning (RL). We propose a psychology theory that is a computational synergy between analogy and RL, in which analogical comparison provides the RL learning algorithm with a measure of relational similarity, and RL provides feedback signals that can drive analogical learning. Simulation results support the power of this approach.