Takuo Matsubara
Bures-Wasserstein Importance-Weighted Evidence Lower Bound: Exposition and Applications
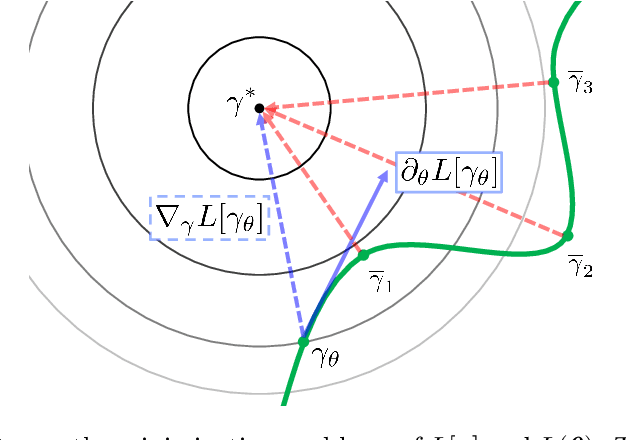
Feb 04, 2026Abstract:The Importance-Weighted Evidence Lower Bound (IW-ELBO) has emerged as an effective objective for variational inference (VI), tightening the standard ELBO and mitigating the mode-seeking behaviour. However, optimizing the IW-ELBO in Euclidean space is often inefficient, as its gradient estimators suffer from a vanishing signal-to-noise ratio (SNR). This paper formulates the optimisation of the IW-ELBO in Bures-Wasserstein space, a manifold of Gaussian distributions equipped with the 2-Wasserstein metric. We derive the Wasserstein gradient of the IW-ELBO and project it onto the Bures-Wasserstein space to yield a tractable algorithm for Gaussian VI. A pivotal contribution of our analysis concerns the stability of the gradient estimator. While the SNR of the standard Euclidean gradient estimator is known to vanish as the number of importance samples $K$ increases, we prove that the SNR of the Wasserstein gradient scales favourably as $Ω(\sqrt{K})$, ensuring optimisation efficiency even for large $K$. We further extend this geometric analysis to the Variational Rényi Importance-Weighted Autoencoder bound, establishing analogous stability guarantees. Experiments demonstrate that the proposed framework achieves superior approximation performance compared to other baselines.
Wasserstein Gradient Boosting: A General Framework with Applications to Posterior Regression
May 15, 2024Abstract:Gradient boosting is a sequential ensemble method that fits a new base learner to the gradient of the remaining loss at each step. We propose a novel family of gradient boosting, Wasserstein gradient boosting, which fits a new base learner to an exactly or approximately available Wasserstein gradient of a loss functional on the space of probability distributions. Wasserstein gradient boosting returns a set of particles that approximates a target probability distribution assigned at each input. In probabilistic prediction, a parametric probability distribution is often specified on the space of output variables, and a point estimate of the output-distribution parameter is produced for each input by a model. Our main application of Wasserstein gradient boosting is a novel distributional estimate of the output-distribution parameter, which approximates the posterior distribution over the output-distribution parameter determined pointwise at each data point. We empirically demonstrate the superior performance of the probabilistic prediction by Wasserstein gradient boosting in comparison with various existing methods.
TCE: A Test-Based Approach to Measuring Calibration Error
Jun 25, 2023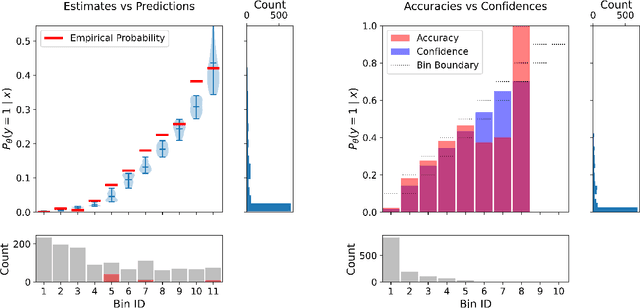

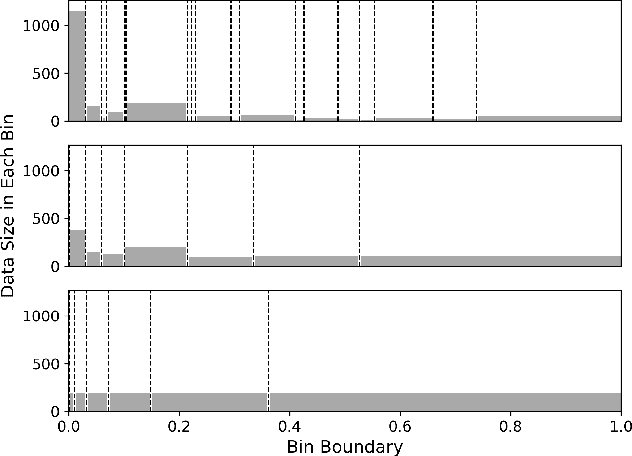
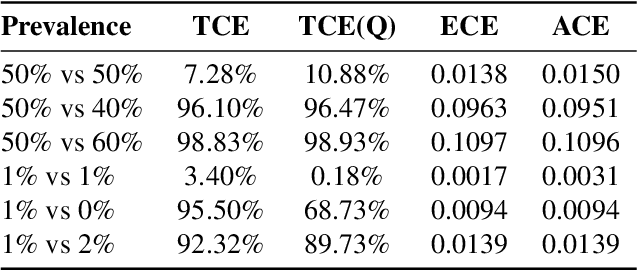
Abstract:This paper proposes a new metric to measure the calibration error of probabilistic binary classifiers, called test-based calibration error (TCE). TCE incorporates a novel loss function based on a statistical test to examine the extent to which model predictions differ from probabilities estimated from data. It offers (i) a clear interpretation, (ii) a consistent scale that is unaffected by class imbalance, and (iii) an enhanced visual representation with repect to the standard reliability diagram. In addition, we introduce an optimality criterion for the binning procedure of calibration error metrics based on a minimal estimation error of the empirical probabilities. We provide a novel computational algorithm for optimal bins under bin-size constraints. We demonstrate properties of TCE through a range of experiments, including multiple real-world imbalanced datasets and ImageNet 1000.
Generalised Bayesian Inference for Discrete Intractable Likelihood
Jun 16, 2022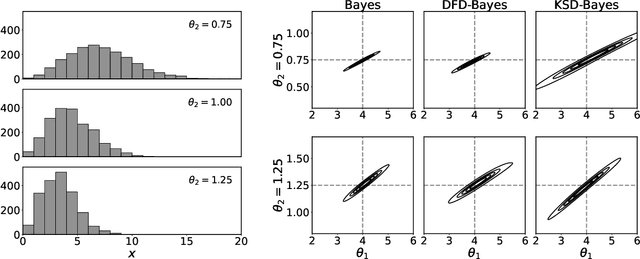
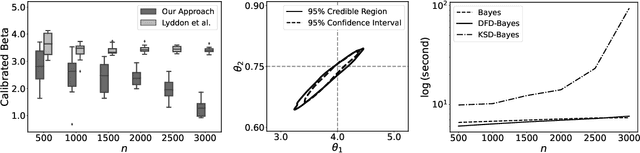
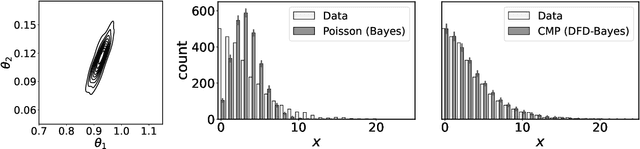
Abstract:Discrete state spaces represent a major computational challenge to statistical inference, since the computation of normalisation constants requires summation over large or possibly infinite sets, which can be impractical. This paper addresses this computational challenge through the development of a novel generalised Bayesian inference procedure suitable for discrete intractable likelihood. Inspired by recent methodological advances for continuous data, the main idea is to update beliefs about model parameters using a discrete Fisher divergence, in lieu of the problematic intractable likelihood. The result is a generalised posterior that can be sampled using standard computational tools, such as Markov chain Monte Carlo, circumventing the intractable normalising constant. The statistical properties of the generalised posterior are analysed, with sufficient conditions for posterior consistency and asymptotic normality established. In addition, a novel and general approach to calibration of generalised posteriors is proposed. Applications are presented on lattice models for discrete spatial data and on multivariate models for count data, where in each case the methodology facilitates generalised Bayesian inference at low computational cost.
Robust Generalised Bayesian Inference for Intractable Likelihoods
Apr 15, 2021



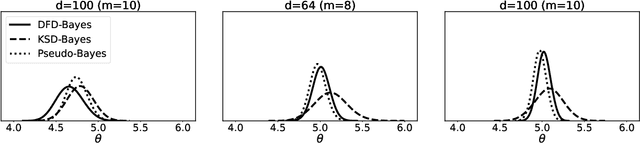
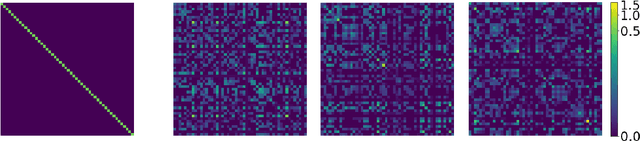
Abstract:Generalised Bayesian inference updates prior beliefs using a loss function, rather than a likelihood, and can therefore be used to confer robustness against possible misspecification of the likelihood. Here we consider generalised Bayesian inference with a Stein discrepancy as a loss function, motivated by applications in which the likelihood contains an intractable normalisation constant. In this context, the Stein discrepancy circumvents evaluation of the normalisation constant and produces generalised posteriors that are either closed form or accessible using standard Markov chain Monte Carlo. On a theoretical level, we show consistency, asymptotic normality, and bias-robustness of the generalised posterior, highlighting how these properties are impacted by the choice of Stein discrepancy. Then, we provide numerical experiments on a range of intractable distributions, including applications to kernel-based exponential family models and non-Gaussian graphical models.
The Ridgelet Prior: A Covariance Function Approach to Prior Specification for Bayesian Neural Networks
Oct 16, 2020


Abstract:Bayesian neural networks attempt to combine the strong predictive performance of neural networks with formal quantification of uncertainty associated with the predictive output in the Bayesian framework. However, it remains unclear how to endow the parameters of the network with a prior distribution that is meaningful when lifted into the output space of the network. A possible solution is proposed that enables the user to posit an appropriate covariance function for the task at hand. Our approach constructs a prior distribution for the parameters of the network, called a ridgelet prior, that approximates the posited covariance structure in the output space of the network. The approach is rooted in the ridgelet transform and we establish both finite-sample-size error bounds and the consistency of the approximation of the covariance function in a limit where the number of hidden units is increased. Our experimental assessment is limited to a proof-of-concept, where we demonstrate that the ridgelet prior can out-perform an unstructured prior on regression problems for which an informative covariance function can be a priori provided.
Integral representation of shallow neural network that attains the global minimum
Oct 10, 2018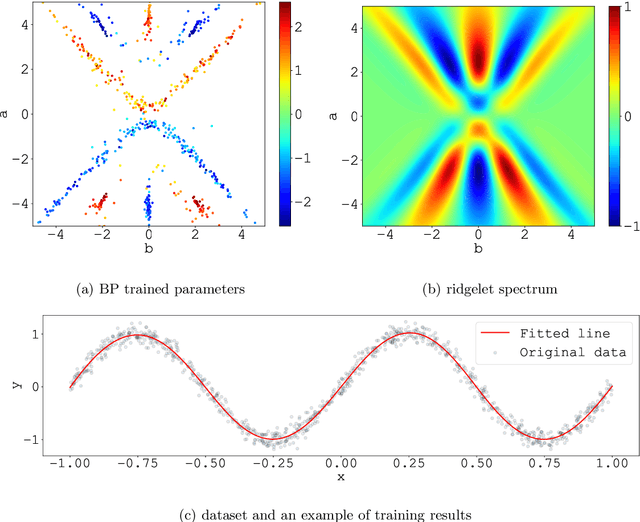
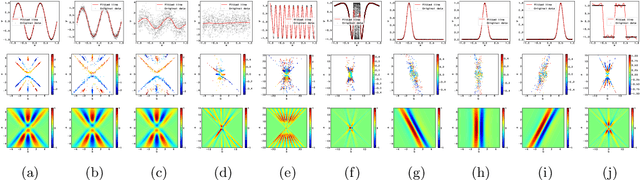
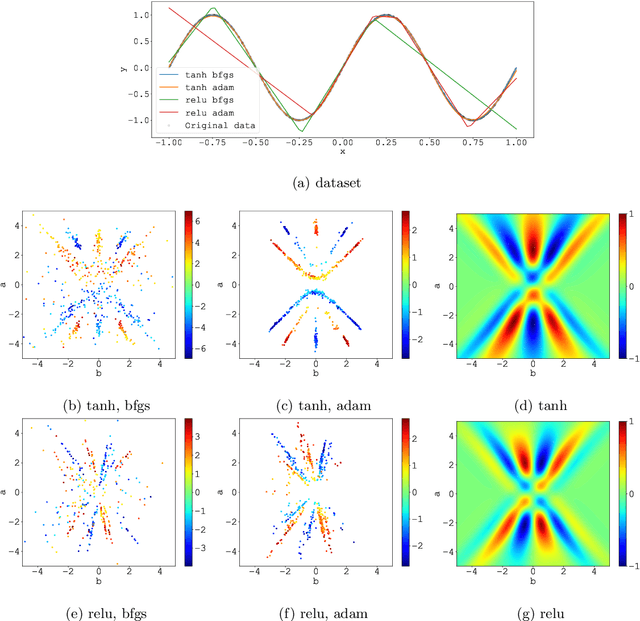
Abstract:We consider the supervised learning problem with shallow neural networks. According to our unpublished experiments conducted several years prior to this study, we had noticed an interesting similarity between the distribution of hidden parameters after backprobagation (BP) training, and the ridgelet spectrum of the same dataset. Therefore, we conjectured that the distribution is expressed as a version of ridgelet transform, but it was not proven until this study. One difficulty is that both the local minimizers and the ridgelet transforms have an infinite number of varieties, and no relations are known between them. By using the integral representation, we reformulate the BP training as a strong-convex optimization problem and find a global minimizer. Finally, by developing ridgelet analysis on a reproducing kernel Hilbert space (RKHS), we write the minimizer explicitly and succeed to prove the conjecture. The modified ridgelet transform has an explicit expression that can be computed by numerical integration, which suggests that we can obtain the global minimizer of BP, without BP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge