Integral representation of shallow neural network that attains the global minimum

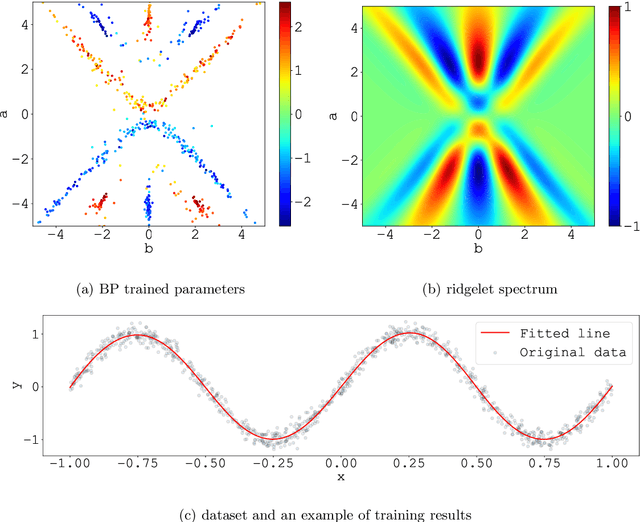
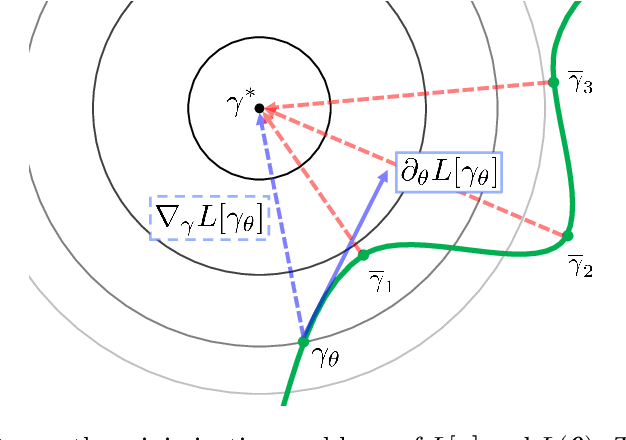
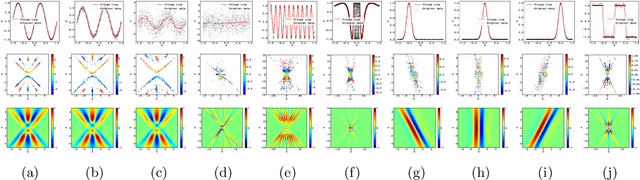
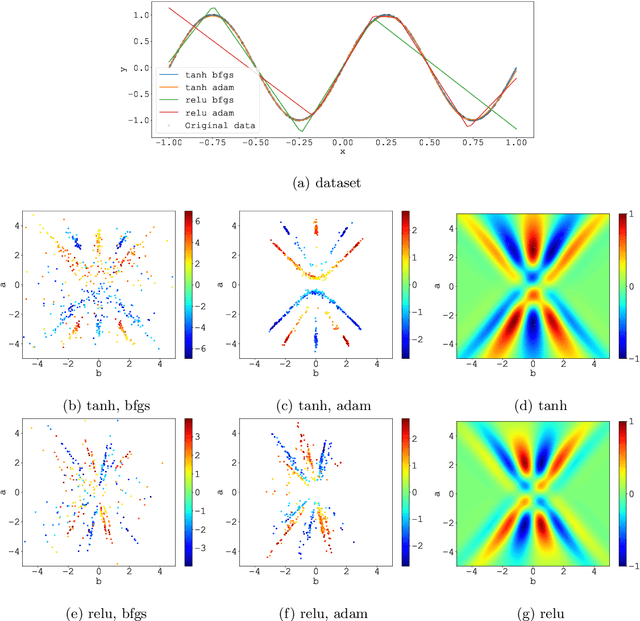
We consider the supervised learning problem with shallow neural networks. According to our unpublished experiments conducted several years prior to this study, we had noticed an interesting similarity between the distribution of hidden parameters after backprobagation (BP) training, and the ridgelet spectrum of the same dataset. Therefore, we conjectured that the distribution is expressed as a version of ridgelet transform, but it was not proven until this study. One difficulty is that both the local minimizers and the ridgelet transforms have an infinite number of varieties, and no relations are known between them. By using the integral representation, we reformulate the BP training as a strong-convex optimization problem and find a global minimizer. Finally, by developing ridgelet analysis on a reproducing kernel Hilbert space (RKHS), we write the minimizer explicitly and succeed to prove the conjecture. The modified ridgelet transform has an explicit expression that can be computed by numerical integration, which suggests that we can obtain the global minimizer of BP, without BP.