Scalable Monte Carlo for Bayesian Learning

This book aims to provide a graduate-level introduction to advanced topics in Markov chain Monte Carlo (MCMC) algorithms, as applied broadly in the Bayesian computational context. Most, if not all of these topics (stochastic gradient MCMC, non-reversible MCMC, continuous time MCMC, and new techniques for convergence assessment) have emerged as recently as the last decade, and have driven substantial recent practical and theoretical advances in the field. A particular focus is on methods that are scalable with respect to either the amount of data, or the data dimension, motivated by the emerging high-priority application areas in machine learning and AI.

Operator-informed score matching for Markov diffusion models

Diffusion models are typically trained using score matching, yet score matching is agnostic to the particular forward process that defines the model. This paper argues that Markov diffusion models enjoy an advantage over other types of diffusion model, as their associated operators can be exploited to improve the training process. In particular, (i) there exists an explicit formal solution to the forward process as a sequence of time-dependent kernel mean embeddings; and (ii) the derivation of score-matching and related estimators can be streamlined. Building upon (i), we propose Riemannian diffusion kernel smoothing, which ameliorates the need for neural score approximation, at least in the low-dimensional context; Building upon (ii), we propose operator-informed score matching, a variance reduction technique that is straightforward to implement in both low- and high-dimensional diffusion modeling and is demonstrated to improve score matching in an empirical proof-of-concept.

Meta-learning Control Variates: Variance Reduction with Limited Data

Control variates can be a powerful tool to reduce the variance of Monte Carlo estimators, but constructing effective control variates can be challenging when the number of samples is small. In this paper, we show that when a large number of related integrals need to be computed, it is possible to leverage the similarity between these integration tasks to improve performance even when the number of samples per task is very small. Our approach, called meta learning CVs (Meta-CVs), can be used for up to hundreds or thousands of tasks. Our empirical assessment indicates that Meta-CVs can lead to significant variance reduction in such settings, and our theoretical analysis establishes general conditions under which Meta-CVs can be successfully trained.

Maximum Likelihood Estimation in Gaussian Process Regression is Ill-Posed

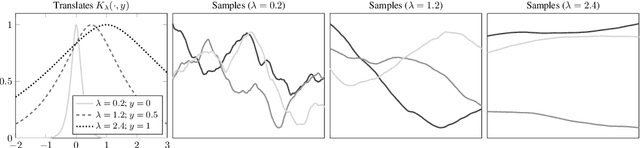
Gaussian process regression underpins countless academic and industrial applications of machine learning and statistics, with maximum likelihood estimation routinely used to select appropriate parameters for the covariance kernel. However, it remains an open problem to establish the circumstances in which maximum likelihood estimation is well-posed. That is, when the predictions of the regression model are continuous (or insensitive to small perturbations) in the training data. This article presents a rigorous proof that the maximum likelihood estimator fails to be well-posed in Hellinger distance in a scenario where the data are noiseless. The failure case occurs for any Gaussian process with a stationary covariance function whose lengthscale parameter is estimated using maximum likelihood. Although the failure of maximum likelihood estimation is informally well-known, these theoretical results appear to be the first of their kind, and suggest that well-posedness may need to be assessed post-hoc, on a case-by-case basis, when maximum likelihood estimation is used to train a Gaussian process model.

Probabilistic Iterative Methods for Linear Systems

This paper presents a probabilistic perspective on iterative methods for approximating the solution $\mathbf{x}_* \in \mathbb{R}^d$ of a nonsingular linear system $\mathbf{A} \mathbf{x}_* = \mathbf{b}$. In the approach a standard iterative method on $\mathbb{R}^d$ is lifted to act on the space of probability distributions $\mathcal{P}(\mathbb{R}^d)$. Classically, an iterative method produces a sequence $\mathbf{x}_m$ of approximations that converge to $\mathbf{x}_*$. The output of the iterative methods proposed in this paper is, instead, a sequence of probability distributions $\mu_m \in \mathcal{P}(\mathbb{R}^d)$. The distributional output both provides a "best guess" for $\mathbf{x}_*$, for example as the mean of $\mu_m$, and also probabilistic uncertainty quantification for the value of $\mathbf{x}_*$ when it has not been exactly determined. Theoretical analysis is provided in the prototypical case of a stationary linear iterative method. In this setting we characterise both the rate of contraction of $\mu_m$ to an atomic measure on $\mathbf{x}_*$ and the nature of the uncertainty quantification being provided. We conclude with an empirical illustration that highlights the insight into solution uncertainty that can be provided by probabilistic iterative methods.

Measure Transport with Kernel Stein Discrepancy

Measure transport underpins several recent algorithms for posterior approximation in the Bayesian context, wherein a transport map is sought to minimise the Kullback--Leibler divergence (KLD) from the posterior to the approximation. The KLD is a strong mode of convergence, requiring absolute continuity of measures and placing restrictions on which transport maps can be permitted. Here we propose to minimise a kernel Stein discrepancy (KSD) instead, requiring only that the set of transport maps is dense in an $L^2$ sense and demonstrating how this condition can be validated. The consistency of the associated posterior approximation is established and empirical results suggest that KSD is competitive and more flexible alternative to KLD for measure transport.

The Ridgelet Prior: A Covariance Function Approach to Prior Specification for Bayesian Neural Networks

Bayesian neural networks attempt to combine the strong predictive performance of neural networks with formal quantification of uncertainty associated with the predictive output in the Bayesian framework. However, it remains unclear how to endow the parameters of the network with a prior distribution that is meaningful when lifted into the output space of the network. A possible solution is proposed that enables the user to posit an appropriate covariance function for the task at hand. Our approach constructs a prior distribution for the parameters of the network, called a ridgelet prior, that approximates the posited covariance structure in the output space of the network. The approach is rooted in the ridgelet transform and we establish both finite-sample-size error bounds and the consistency of the approximation of the covariance function in a limit where the number of hidden units is increased. Our experimental assessment is limited to a proof-of-concept, where we demonstrate that the ridgelet prior can out-perform an unstructured prior on regression problems for which an informative covariance function can be a priori provided.

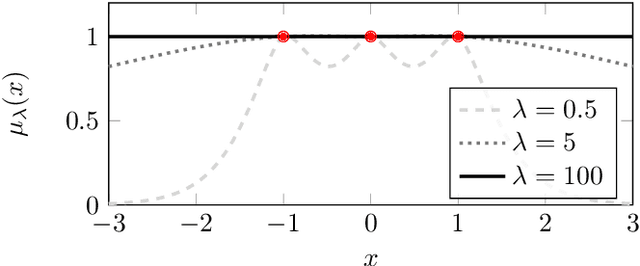
Maximum likelihood estimation and uncertainty quantification for Gaussian process approximation of deterministic functions

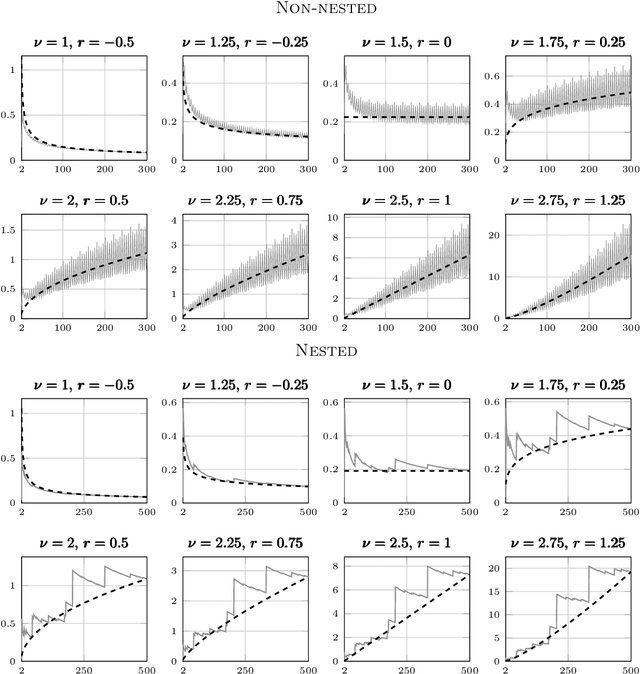
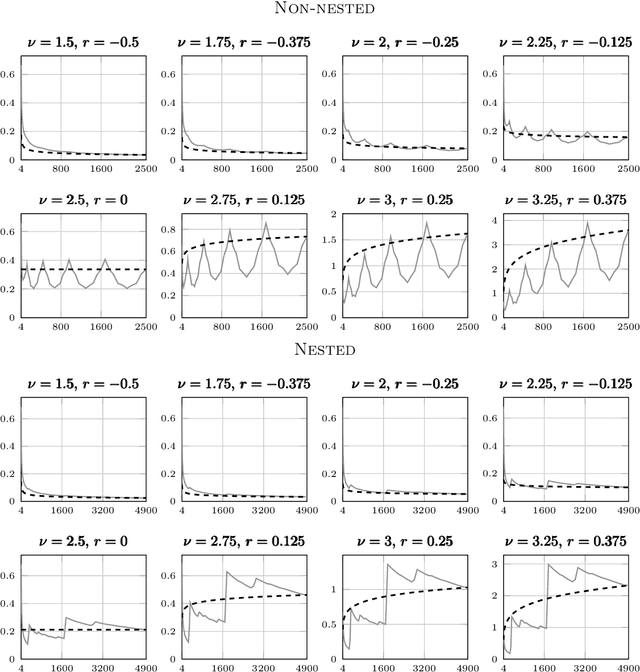
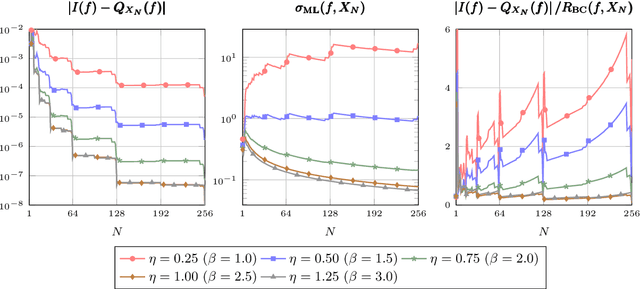
Despite the ubiquity of the Gaussian process regression model, few theoretical results are available that account for the fact that parameters of the covariance kernel typically need to be estimated from the dataset. This article provides one of the first theoretical analyses in the context of Gaussian process regression with a noiseless dataset. Specifically, we consider the scenario where the scale parameter of a Sobolev kernel (such as a Mat\'ern kernel) is estimated by maximum likelihood. We show that the maximum likelihood estimation of the scale parameter alone provides significant adaptation against misspecification of the Gaussian process model in the sense that the model can become "slowly" overconfident at worst, regardless of the difference between the smoothness of the data-generating function and that expected by the model. The analysis is based on a combination of techniques from nonparametric regression and scattered data interpolation. Empirical results are provided in support of the theoretical findings.

Improved Calibration of Numerical Integration Error in Sigma-Point Filters

The sigma-point filters, such as the UKF, which exploit numerical quadrature to obtain an additional order of accuracy in the moment transformation step, are popular alternatives to the ubiquitous EKF. The classical quadrature rules used in the sigma-point filters are motivated via polynomial approximation of the integrand, however in the applied context these assumptions cannot always be justified. As a result, quadrature error can introduce bias into estimated moments, for which there is no compensatory mechanism in the classical sigma-point filters. This can lead in turn to estimates and predictions that are poorly calibrated. In this article, we investigate the Bayes-Sard quadrature method in the context of sigma-point filters, which enables uncertainty due to quadrature error to be formalised within a probabilistic model. Our first contribution is to derive the well-known classical quadratures as special cases of the Bayes-Sard quadrature method. Then a general-purpose moment transform is developed and utilised in the design of novel sigma-point filters, so that uncertainty due to quadrature error is explicitly quantified. Numerical experiments on a challenging tracking example with misspecified initial conditions show that the additional uncertainty quantification built into our method leads to better-calibrated state estimates with improved RMSE.

Rejoinder for "Probabilistic Integration: A Role in Statistical Computation?"

This article is the rejoinder for the paper "Probabilistic Integration: A Role in Statistical Computation?" to appear in Statistical Science with discussion. We would first like to thank the reviewers and many of our colleagues who helped shape this paper, the editor for selecting our paper for discussion, and of course all of the discussants for their thoughtful, insightful and constructive comments. In this rejoinder, we respond to some of the points raised by the discussants and comment further on the fundamental questions underlying the paper: (i) Should Bayesian ideas be used in numerical analysis?, and (ii) If so, what role should such approaches have in statistical computation?