Stochastic Rounding Implicitly Regularizes Tall-and-Thin Matrices

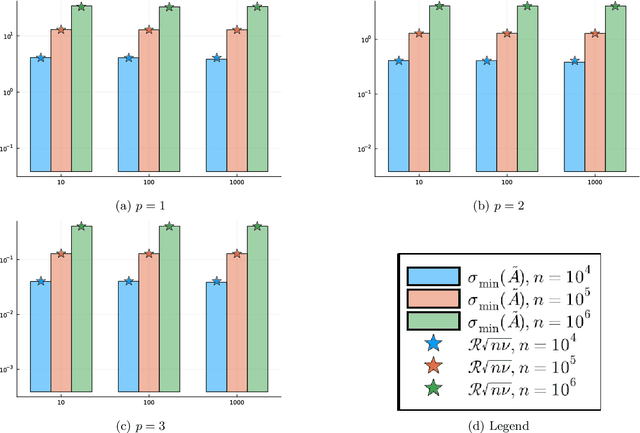
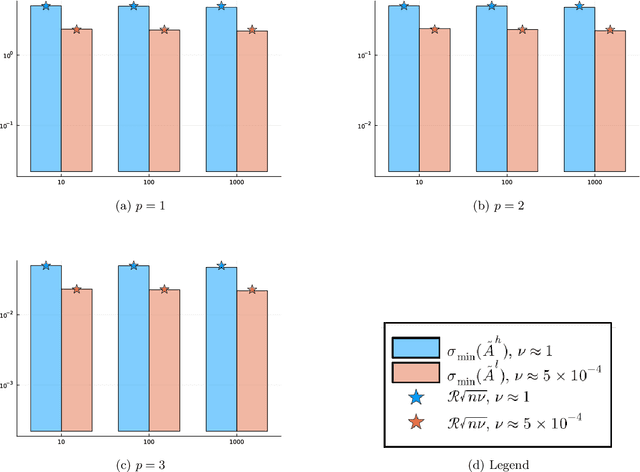
Motivated by the popularity of stochastic rounding in the context of machine learning and the training of large-scale deep neural network models, we consider stochastic nearness rounding of real matrices $\mathbf{A}$ with many more rows than columns. We provide novel theoretical evidence, supported by extensive experimental evaluation that, with high probability, the smallest singular value of a stochastically rounded matrix is well bounded away from zero -- regardless of how close $\mathbf{A}$ is to being rank deficient and even if $\mathbf{A}$ is rank-deficient. In other words, stochastic rounding \textit{implicitly regularizes} tall and skinny matrices $\mathbf{A}$ so that the rounded version has full column rank. Our proofs leverage powerful results in random matrix theory, and the idea that stochastic rounding errors do not concentrate in low-dimensional column spaces.

Probabilistic Iterative Methods for Linear Systems

This paper presents a probabilistic perspective on iterative methods for approximating the solution $\mathbf{x}_* \in \mathbb{R}^d$ of a nonsingular linear system $\mathbf{A} \mathbf{x}_* = \mathbf{b}$. In the approach a standard iterative method on $\mathbb{R}^d$ is lifted to act on the space of probability distributions $\mathcal{P}(\mathbb{R}^d)$. Classically, an iterative method produces a sequence $\mathbf{x}_m$ of approximations that converge to $\mathbf{x}_*$. The output of the iterative methods proposed in this paper is, instead, a sequence of probability distributions $\mu_m \in \mathcal{P}(\mathbb{R}^d)$. The distributional output both provides a "best guess" for $\mathbf{x}_*$, for example as the mean of $\mu_m$, and also probabilistic uncertainty quantification for the value of $\mathbf{x}_*$ when it has not been exactly determined. Theoretical analysis is provided in the prototypical case of a stationary linear iterative method. In this setting we characterise both the rate of contraction of $\mu_m$ to an atomic measure on $\mathbf{x}_*$ and the nature of the uncertainty quantification being provided. We conclude with an empirical illustration that highlights the insight into solution uncertainty that can be provided by probabilistic iterative methods.

Randomized Least Squares Regression: Combining Model- and Algorithm-Induced Uncertainties

We analyze the uncertainties in the minimum norm solution of full-rank regression problems, arising from Gaussian linear models, computed by randomized (row-wise sampling and, more generally, sketching) algorithms. From a deterministic perspective, our structural perturbation bounds imply that least squares problems are less sensitive to multiplicative perturbations than to additive perturbations. From a probabilistic perspective, our expressions for the total expectation and variance with regard to both model- and algorithm-induced uncertainties, are exact, hold for general sketching matrices, and make no assumptions on the rank of the sketched matrix. The relative differences between the total bias and variance on the one hand, and the model bias and variance on the other hand, are governed by two factors: (i) the expected rank deficiency of the sketched matrix, and (ii) the expected difference between projectors associated with the original and the sketched problems. A simple example, based on uniform sampling with replacement, illustrates the statistical quantities.

Randomized Approximation of the Gram Matrix: Exact Computation and Probabilistic Bounds

Given a real matrix A with n columns, the problem is to approximate the Gram product AA^T by c << n weighted outer products of columns of A. Necessary and sufficient conditions for the exact computation of AA^T (in exact arithmetic) from c >= rank(A) columns depend on the right singular vector matrix of A. For a Monte-Carlo matrix multiplication algorithm by Drineas et al. that samples outer products, we present probabilistic bounds for the 2-norm relative error due to randomization. The bounds depend on the stable rank or the rank of A, but not on the matrix dimensions. Numerical experiments illustrate that the bounds are informative, even for stringent success probabilities and matrices of small dimension. We also derive bounds for the smallest singular value and the condition number of matrices obtained by sampling rows from orthonormal matrices.