Stochastic Rounding Increases Small Singular Values

Over the past half-dozen years, stochastic rounding (SR) has regained significant attention as a quantization scheme for low-precision floating-point arithmetic, with applications spanning numerical analysis and modern machine learning systems. Recent work has shown that SR acts as an implicit regularizer by increasing the smallest singular value of extremely tall-and-thin (or, symmetrically, short-and-fat) matrices. In this work, we substantially sharpen and extend this understanding in two directions. First, we show that the regularization effect of SR is not restricted to extreme aspect ratio regimes: it persists for matrices with constant aspect ratio. Second, we demonstrate that SR does not merely regularize the smallest singular value, but instead lifts entire clusters of singular values at the tail of the spectrum. Together, these results provide a more general characterization of stochastic rounding as a spectral regularizer, revealing that its effects extend beyond extremal aspect ratios and act on a broader portion of the singular value spectrum.

Stochastic Rounding Implicitly Regularizes Tall-and-Thin Matrices

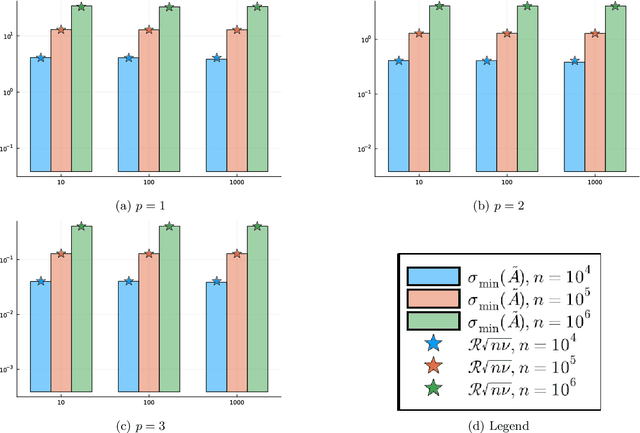
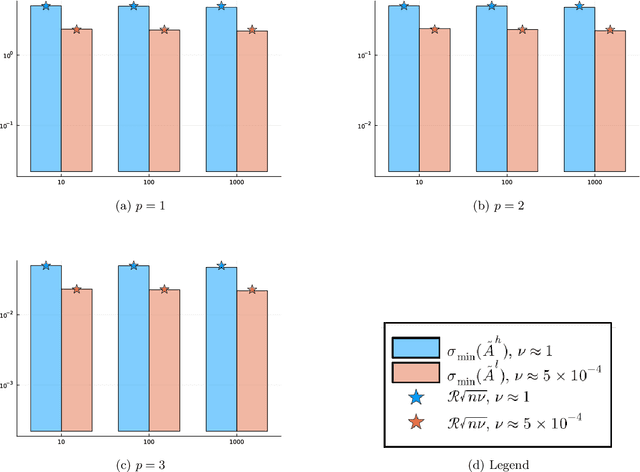
Motivated by the popularity of stochastic rounding in the context of machine learning and the training of large-scale deep neural network models, we consider stochastic nearness rounding of real matrices $\mathbf{A}$ with many more rows than columns. We provide novel theoretical evidence, supported by extensive experimental evaluation that, with high probability, the smallest singular value of a stochastically rounded matrix is well bounded away from zero -- regardless of how close $\mathbf{A}$ is to being rank deficient and even if $\mathbf{A}$ is rank-deficient. In other words, stochastic rounding \textit{implicitly regularizes} tall and skinny matrices $\mathbf{A}$ so that the rounded version has full column rank. Our proofs leverage powerful results in random matrix theory, and the idea that stochastic rounding errors do not concentrate in low-dimensional column spaces.