Stochastic Rounding Implicitly Regularizes Tall-and-Thin Matrices
Paper and Code
Mar 18, 2024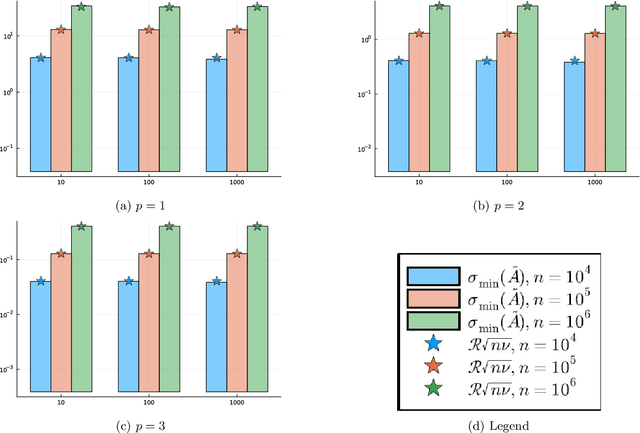
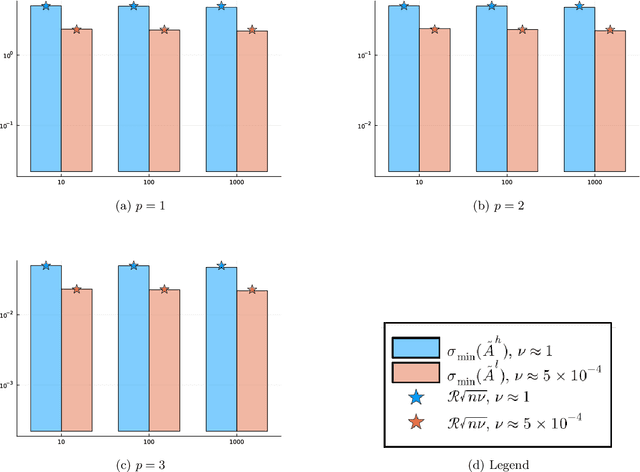

Motivated by the popularity of stochastic rounding in the context of machine learning and the training of large-scale deep neural network models, we consider stochastic nearness rounding of real matrices $\mathbf{A}$ with many more rows than columns. We provide novel theoretical evidence, supported by extensive experimental evaluation that, with high probability, the smallest singular value of a stochastically rounded matrix is well bounded away from zero -- regardless of how close $\mathbf{A}$ is to being rank deficient and even if $\mathbf{A}$ is rank-deficient. In other words, stochastic rounding \textit{implicitly regularizes} tall and skinny matrices $\mathbf{A}$ so that the rounded version has full column rank. Our proofs leverage powerful results in random matrix theory, and the idea that stochastic rounding errors do not concentrate in low-dimensional column spaces.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge