Stochastic Rounding Implicitly Regularizes Tall-and-Thin Matrices

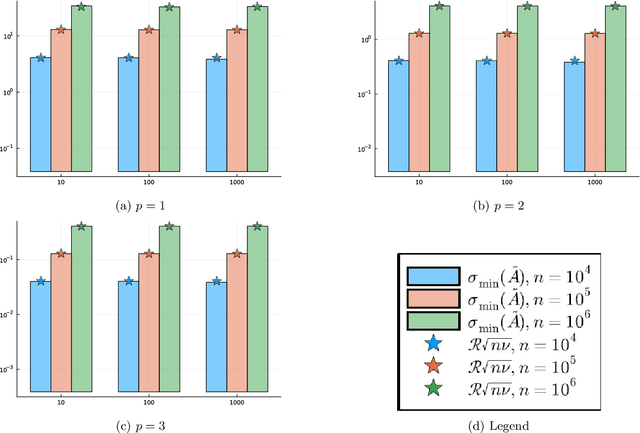
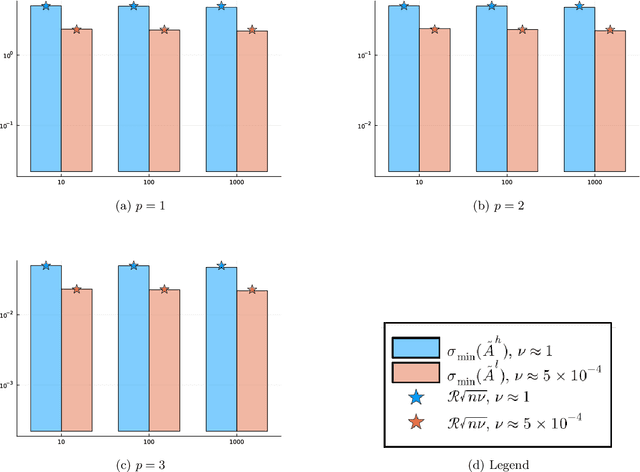
Motivated by the popularity of stochastic rounding in the context of machine learning and the training of large-scale deep neural network models, we consider stochastic nearness rounding of real matrices $\mathbf{A}$ with many more rows than columns. We provide novel theoretical evidence, supported by extensive experimental evaluation that, with high probability, the smallest singular value of a stochastically rounded matrix is well bounded away from zero -- regardless of how close $\mathbf{A}$ is to being rank deficient and even if $\mathbf{A}$ is rank-deficient. In other words, stochastic rounding \textit{implicitly regularizes} tall and skinny matrices $\mathbf{A}$ so that the rounded version has full column rank. Our proofs leverage powerful results in random matrix theory, and the idea that stochastic rounding errors do not concentrate in low-dimensional column spaces.

Refined Mechanism Design for Approximately Structured Priors via Active Regression

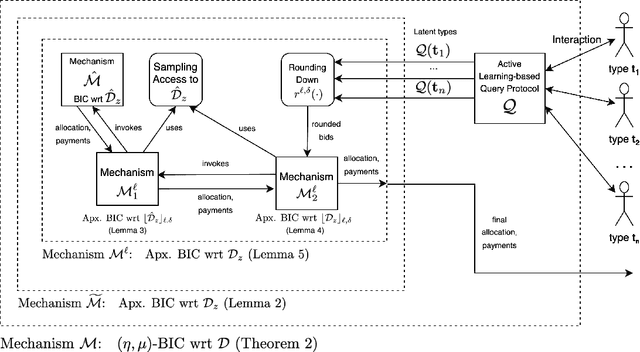
We consider the problem of a revenue-maximizing seller with a large number of items $m$ for sale to $n$ strategic bidders, whose valuations are drawn independently from high-dimensional, unknown prior distributions. It is well-known that optimal and even approximately-optimal mechanisms for this setting are notoriously difficult to characterize or compute, and, even when they can be found, are often rife with various counter-intuitive properties. In this paper, following a model introduced recently by Cai and Daskalakis~\cite{cai2022recommender}, we consider the case that bidders' prior distributions can be well-approximated by a topic model. We design an active learning component, responsible for interacting with the bidders and outputting low-dimensional approximations of their types, and a mechanism design component, responsible for robustifying mechanisms for the low-dimensional model to work for the approximate types of the former component. On the active learning front, we cast our problem in the framework of Randomized Linear Algebra (RLA) for regression problems, allowing us to import several breakthrough results from that line of research, and adapt them to our setting. On the mechanism design front, we remove many restrictive assumptions of prior work on the type of access needed to the underlying distributions and the associated mechanisms. To the best of our knowledge, our work is the first to formulate connections between mechanism design, and RLA for active learning of regression problems, opening the door for further applications of randomized linear algebra primitives to mechanism design.