Automating Food Drop: The Power of Two Choices for Dynamic and Fair Food Allocation

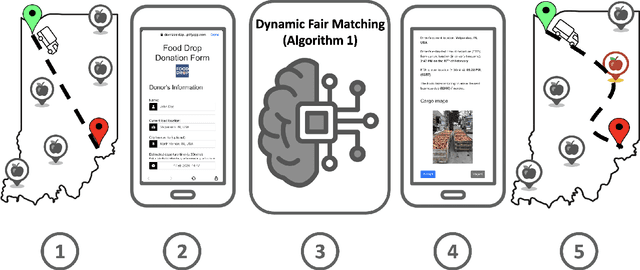
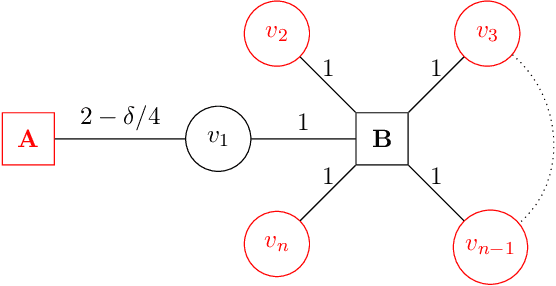
Food waste and food insecurity are two closely related pressing global issues. Food rescue organizations worldwide run programs aimed at addressing the two problems. In this paper, we partner with a non-profit organization in the state of Indiana that leads \emph{Food Drop}, a program that is designed to redirect rejected truckloads of food away from landfills and into food banks. The truckload to food bank matching decisions are currently made by an employee of our partner organization. In addition to this being a very time-consuming task, as perhaps expected from human-based matching decisions, the allocations are often skewed: a small percentage of the possible recipients receives the majority of donations. Our goal in this partnership is to completely automate Food Drop. In doing so, we need a matching algorithm for making real-time decisions that strikes a balance between ensuring fairness for the food banks that receive the food and optimizing efficiency for the truck drivers. In this paper, we describe the theoretical guarantees and experiments that dictated our choice of algorithm in the platform we built and deployed for our partner organization. Our work also makes contributions to the literature on load balancing and balls-into-bins games, that might be of independent interest. Specifically, we study the allocation of $m$ weighted balls into $n$ weighted bins, where each ball has two non-uniformly sampled random bin choices, and prove upper bounds, that hold with high probability, on the maximum load of any bin.

Refined Mechanism Design for Approximately Structured Priors via Active Regression

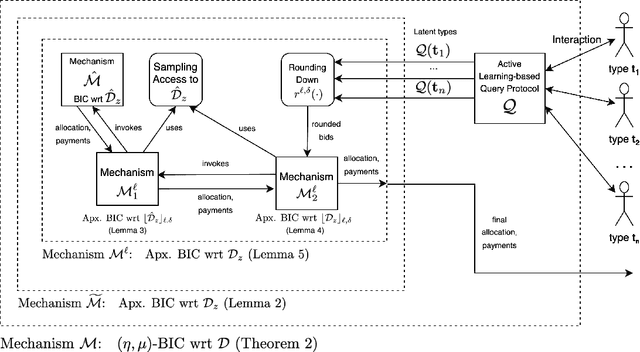
We consider the problem of a revenue-maximizing seller with a large number of items $m$ for sale to $n$ strategic bidders, whose valuations are drawn independently from high-dimensional, unknown prior distributions. It is well-known that optimal and even approximately-optimal mechanisms for this setting are notoriously difficult to characterize or compute, and, even when they can be found, are often rife with various counter-intuitive properties. In this paper, following a model introduced recently by Cai and Daskalakis~\cite{cai2022recommender}, we consider the case that bidders' prior distributions can be well-approximated by a topic model. We design an active learning component, responsible for interacting with the bidders and outputting low-dimensional approximations of their types, and a mechanism design component, responsible for robustifying mechanisms for the low-dimensional model to work for the approximate types of the former component. On the active learning front, we cast our problem in the framework of Randomized Linear Algebra (RLA) for regression problems, allowing us to import several breakthrough results from that line of research, and adapt them to our setting. On the mechanism design front, we remove many restrictive assumptions of prior work on the type of access needed to the underlying distributions and the associated mechanisms. To the best of our knowledge, our work is the first to formulate connections between mechanism design, and RLA for active learning of regression problems, opening the door for further applications of randomized linear algebra primitives to mechanism design.