Maximum Likelihood Estimation in Gaussian Process Regression is Ill-Posed

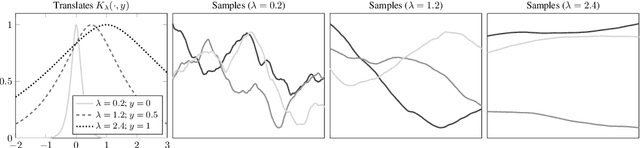
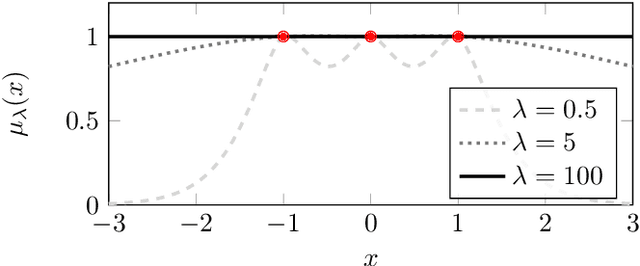
Gaussian process regression underpins countless academic and industrial applications of machine learning and statistics, with maximum likelihood estimation routinely used to select appropriate parameters for the covariance kernel. However, it remains an open problem to establish the circumstances in which maximum likelihood estimation is well-posed. That is, when the predictions of the regression model are continuous (or insensitive to small perturbations) in the training data. This article presents a rigorous proof that the maximum likelihood estimator fails to be well-posed in Hellinger distance in a scenario where the data are noiseless. The failure case occurs for any Gaussian process with a stationary covariance function whose lengthscale parameter is estimated using maximum likelihood. Although the failure of maximum likelihood estimation is informally well-known, these theoretical results appear to be the first of their kind, and suggest that well-posedness may need to be assessed post-hoc, on a case-by-case basis, when maximum likelihood estimation is used to train a Gaussian process model.