Scalable Monte Carlo for Bayesian Learning

This book aims to provide a graduate-level introduction to advanced topics in Markov chain Monte Carlo (MCMC) algorithms, as applied broadly in the Bayesian computational context. Most, if not all of these topics (stochastic gradient MCMC, non-reversible MCMC, continuous time MCMC, and new techniques for convergence assessment) have emerged as recently as the last decade, and have driven substantial recent practical and theoretical advances in the field. A particular focus is on methods that are scalable with respect to either the amount of data, or the data dimension, motivated by the emerging high-priority application areas in machine learning and AI.

SwISS: A Scalable Markov chain Monte Carlo Divide-and-Conquer Strategy

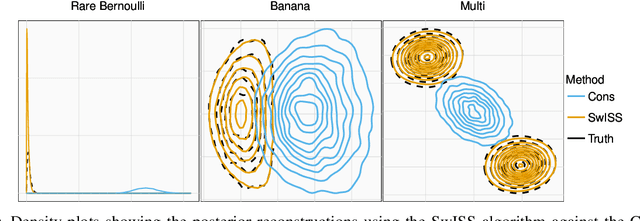
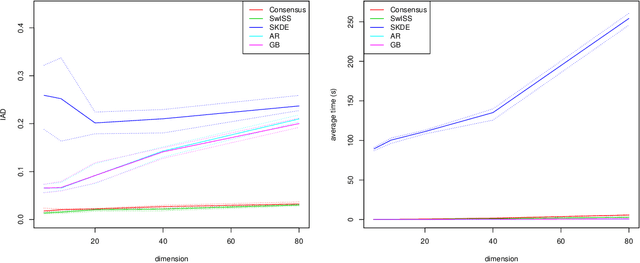
Divide-and-conquer strategies for Monte Carlo algorithms are an increasingly popular approach to making Bayesian inference scalable to large data sets. In its simplest form, the data are partitioned across multiple computing cores and a separate Markov chain Monte Carlo algorithm on each core targets the associated partial posterior distribution, which we refer to as a sub-posterior, that is the posterior given only the data from the segment of the partition associated with that core. Divide-and-conquer techniques reduce computational, memory and disk bottle-necks, but make it difficult to recombine the sub-posterior samples. We propose SwISS: Sub-posteriors with Inflation, Scaling and Shifting; a new approach for recombining the sub-posterior samples which is simple to apply, scales to high-dimensional parameter spaces and accurately approximates the original posterior distribution through affine transformations of the sub-posterior samples. We prove that our transformation is asymptotically optimal across a natural set of affine transformations and illustrate the efficacy of SwISS against competing algorithms on synthetic and real-world data sets.

Bounds on Wasserstein distances between continuous distributions using independent samples

The plug-in estimator of the Wasserstein distance is known to be conservative, however its usefulness is severely limited when the distributions are similar as its bias does not decay to zero with the true Wasserstein distance. We propose a linear combination of plug-in estimators for the squared 2-Wasserstein distance with a reduced bias that decays to zero with the true distance. The new estimator is provably conservative provided one distribution is appropriately overdispersed with respect the other, and is unbiased when the distributions are equal. We apply it to approximately bound from above the 2-Wasserstein distance between the target and current distribution in Markov chain Monte Carlo, running multiple identically distributed chains which start, and remain, overdispersed with respect to the target. Our bound consistently outperforms the current state-of-the-art bound, which uses coupling, improving mixing time bounds by up to an order of magnitude.

Merging MCMC Subposteriors through Gaussian-Process Approximations

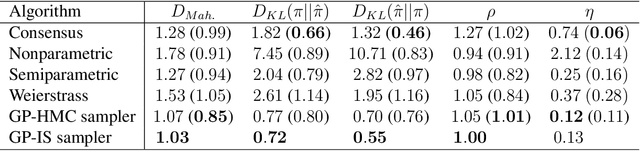
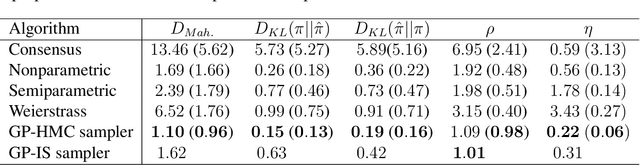
Markov chain Monte Carlo (MCMC) algorithms have become powerful tools for Bayesian inference. However, they do not scale well to large-data problems. Divide-and-conquer strategies, which split the data into batches and, for each batch, run independent MCMC algorithms targeting the corresponding subposterior, can spread the computational burden across a number of separate workers. The challenge with such strategies is in recombining the subposteriors to approximate the full posterior. By creating a Gaussian-process approximation for each log-subposterior density we create a tractable approximation for the full posterior. This approximation is exploited through three methodologies: firstly a Hamiltonian Monte Carlo algorithm targeting the expectation of the posterior density provides a sample from an approximation to the posterior; secondly, evaluating the true posterior at the sampled points leads to an importance sampler that, asymptotically, targets the true posterior expectations; finally, an alternative importance sampler uses the full Gaussian-process distribution of the approximation to the log-posterior density to re-weight any initial sample and provide both an estimate of the posterior expectation and a measure of the uncertainty in it.

Particle Metropolis-adjusted Langevin algorithms

This paper proposes a new sampling scheme based on Langevin dynamics that is applicable within pseudo-marginal and particle Markov chain Monte Carlo algorithms. We investigate this algorithm's theoretical properties under standard asymptotics, which correspond to an increasing dimension of the parameters, $n$. Our results show that the behaviour of the algorithm depends crucially on how accurately one can estimate the gradient of the log target density. If the error in the estimate of the gradient is not sufficiently controlled as dimension increases, then asymptotically there will be no advantage over the simpler random-walk algorithm. However, if the error is sufficiently well-behaved, then the optimal scaling of this algorithm will be $O(n^{-1/6})$ compared to $O(n^{-1/2})$ for the random walk. Our theory also gives guidelines on how to tune the number of Monte Carlo samples in the likelihood estimate and the proposal step-size.