SwISS: A Scalable Markov chain Monte Carlo Divide-and-Conquer Strategy
Paper and Code
Aug 08, 2022
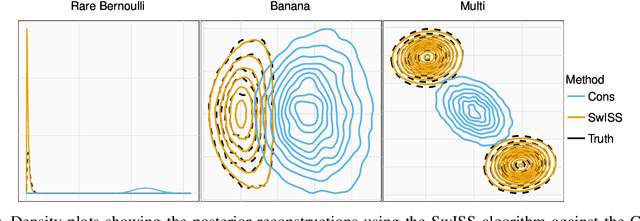

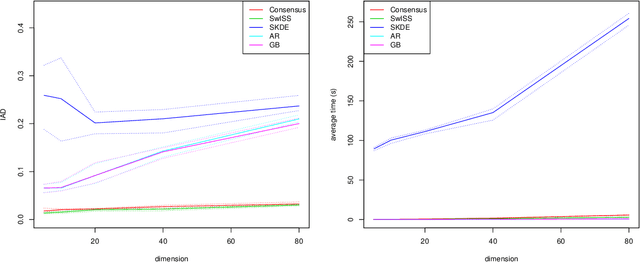
Divide-and-conquer strategies for Monte Carlo algorithms are an increasingly popular approach to making Bayesian inference scalable to large data sets. In its simplest form, the data are partitioned across multiple computing cores and a separate Markov chain Monte Carlo algorithm on each core targets the associated partial posterior distribution, which we refer to as a sub-posterior, that is the posterior given only the data from the segment of the partition associated with that core. Divide-and-conquer techniques reduce computational, memory and disk bottle-necks, but make it difficult to recombine the sub-posterior samples. We propose SwISS: Sub-posteriors with Inflation, Scaling and Shifting; a new approach for recombining the sub-posterior samples which is simple to apply, scales to high-dimensional parameter spaces and accurately approximates the original posterior distribution through affine transformations of the sub-posterior samples. We prove that our transformation is asymptotically optimal across a natural set of affine transformations and illustrate the efficacy of SwISS against competing algorithms on synthetic and real-world data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge