Maximum likelihood estimation and uncertainty quantification for Gaussian process approximation of deterministic functions

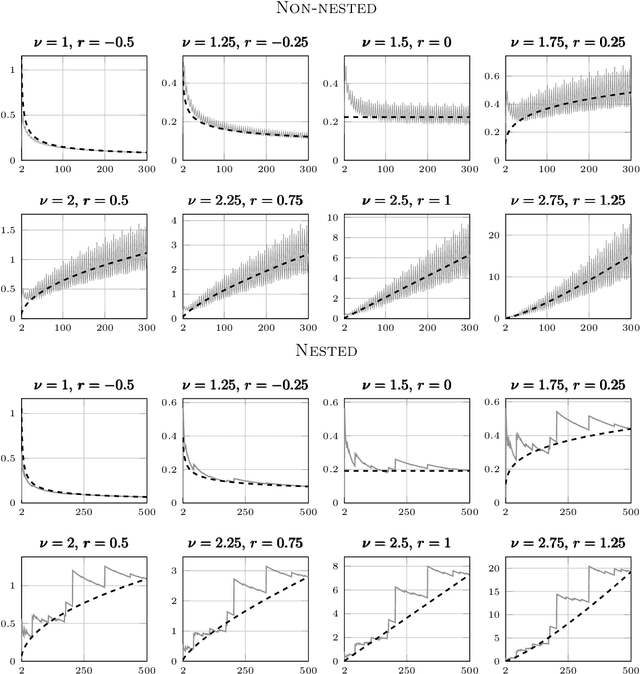
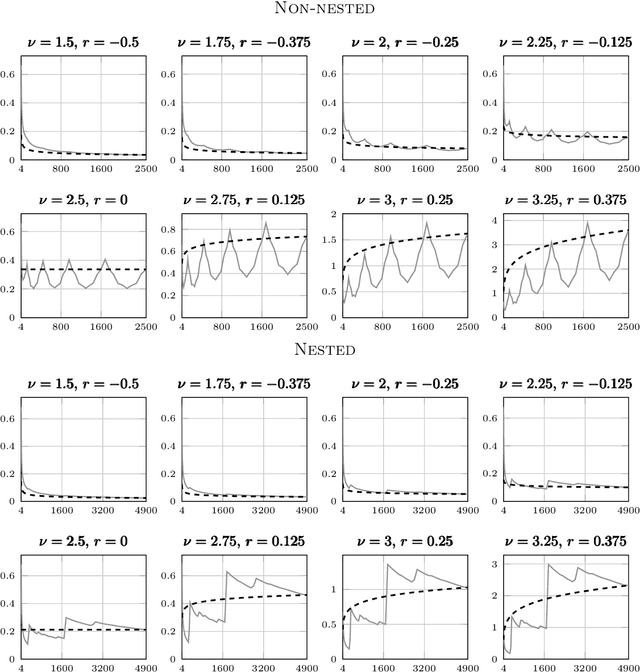
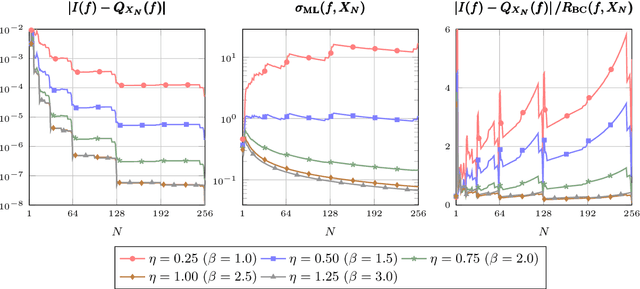
Despite the ubiquity of the Gaussian process regression model, few theoretical results are available that account for the fact that parameters of the covariance kernel typically need to be estimated from the dataset. This article provides one of the first theoretical analyses in the context of Gaussian process regression with a noiseless dataset. Specifically, we consider the scenario where the scale parameter of a Sobolev kernel (such as a Mat\'ern kernel) is estimated by maximum likelihood. We show that the maximum likelihood estimation of the scale parameter alone provides significant adaptation against misspecification of the Gaussian process model in the sense that the model can become "slowly" overconfident at worst, regardless of the difference between the smoothness of the data-generating function and that expected by the model. The analysis is based on a combination of techniques from nonparametric regression and scattered data interpolation. Empirical results are provided in support of the theoretical findings.