Flexible Tails for Normalizing Flows

Normalizing flows are a flexible class of probability distributions, expressed as transformations of a simple base distribution. A limitation of standard normalizing flows is representing distributions with heavy tails, which arise in applications to both density estimation and variational inference. A popular current solution to this problem is to use a heavy tailed base distribution. Examples include the tail adaptive flow (TAF) methods of Laszkiewicz et al (2022). We argue this can lead to poor performance due to the difficulty of optimising neural networks, such as normalizing flows, under heavy tailed input. This problem is demonstrated in our paper. We propose an alternative: use a Gaussian base distribution and a final transformation layer which can produce heavy tails. We call this approach tail transform flow (TTF). Experimental results show this approach outperforms current methods, especially when the target distribution has large dimension or tail weight.

Flexible Tails for Normalising Flows, with Application to the Modelling of Financial Return Data

We propose a transformation capable of altering the tail properties of a distribution, motivated by extreme value theory, which can be used as a layer in a normalizing flow to approximate multivariate heavy tailed distributions. We apply this approach to model financial returns, capturing potentially extreme shocks that arise in such data. The trained models can be used directly to generate new synthetic sets of potentially extreme returns

Measure Transport with Kernel Stein Discrepancy

Measure transport underpins several recent algorithms for posterior approximation in the Bayesian context, wherein a transport map is sought to minimise the Kullback--Leibler divergence (KLD) from the posterior to the approximation. The KLD is a strong mode of convergence, requiring absolute continuity of measures and placing restrictions on which transport maps can be permitted. Here we propose to minimise a kernel Stein discrepancy (KSD) instead, requiring only that the set of transport maps is dense in an $L^2$ sense and demonstrating how this condition can be validated. The consistency of the associated posterior approximation is established and empirical results suggest that KSD is competitive and more flexible alternative to KLD for measure transport.

Bonsai-Net: One-Shot Neural Architecture Search via Differentiable Pruners

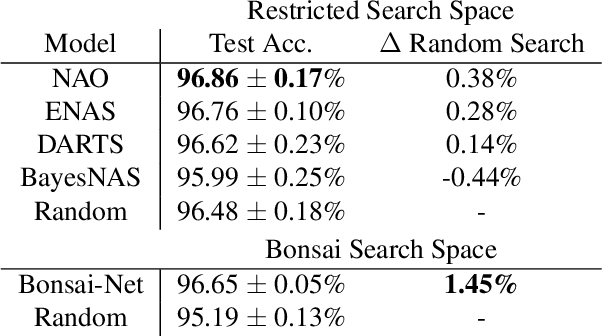
One-shot Neural Architecture Search (NAS) aims to minimize the computational expense of discovering state-of-the-art models. However, in the past year attention has been drawn to the comparable performance of naive random search across the same search spaces used by leading NAS algorithms. To address this, we explore the effects of drastically relaxing the NAS search space, and we present Bonsai-Net, an efficient one-shot NAS method to explore our relaxed search space. Bonsai-Net is built around a modified differential pruner and can consistently discover state-of-the-art architectures that are significantly better than random search with fewer parameters than other state-of-the-art methods. Additionally, Bonsai-Net performs simultaneous model search and training, dramatically reducing the total time it takes to generate fully-trained models from scratch.

Distilling importance sampling

The two main approaches to Bayesian inference are sampling and optimisation methods. However many complicated posteriors are difficult to approximate by either. Therefore we propose a novel approach combining features of both. We use a flexible parameterised family of densities, such as a normalising flow. Given a density from this family approximating the posterior we use importance sampling to produce a weighted sample from a more accurate posterior approximation. This sample is then used in optimisation to update the parameters of the approximate density, a process we refer to as "distilling" the importance sampling results. We illustrate our method in a queueing model example.

Scalable approximate inference for state space models with normalising flows

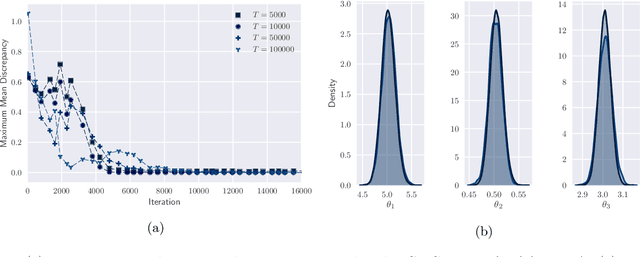
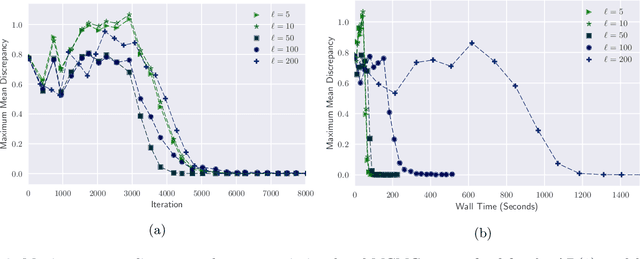
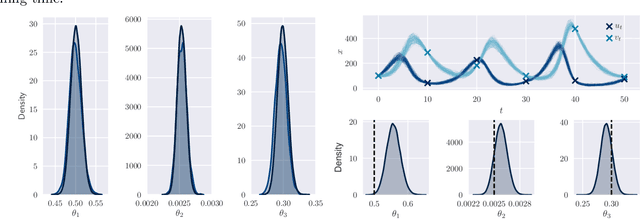
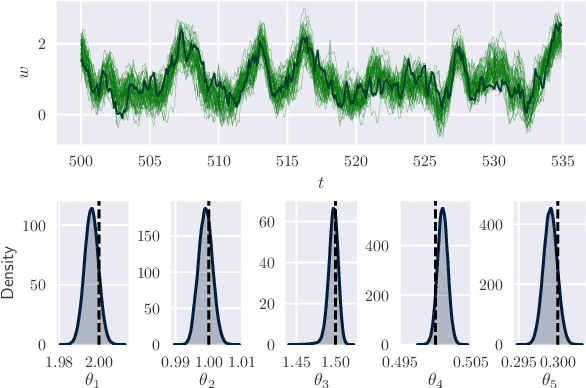
By exploiting mini-batch stochastic gradient optimisation, variational inference has had great success in scaling up approximate Bayesian inference to big data. To date, however, this strategy has only been applicable to models of independent data. Here we extend mini-batch variational methods to state space models of time series data. To do so we introduce a novel generative model as our variational approximation, a local inverse autoregressive flow. This allows a subsequence to be sampled without sampling the entire distribution. Hence we can perform training iterations using short portions of the time series at low computational cost. We illustrate our method on AR(1), Lotka-Volterra and FitzHugh-Nagumo models, achieving accurate parameter estimation in a short time.

Variational Bridge Constructs for Grey Box Modelling with Gaussian Processes

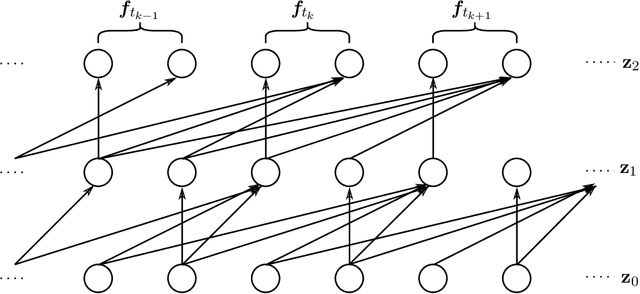
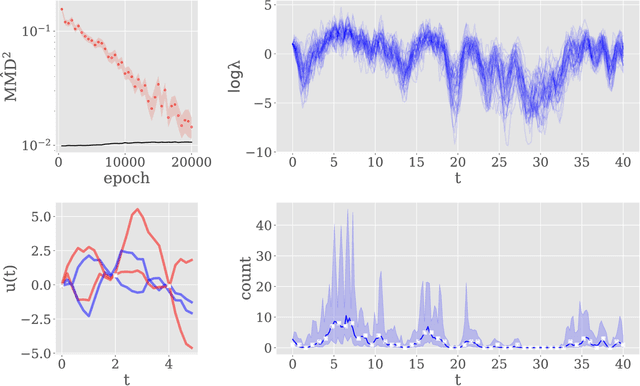
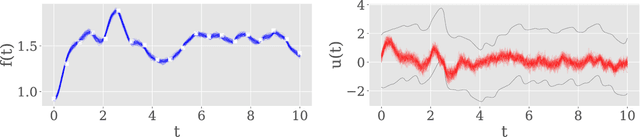
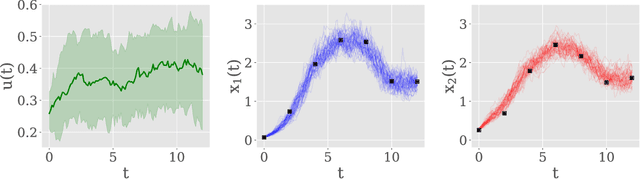
This paper introduces a method for inference of heterogeneous dynamical systems where part of the dynamics are known, in the form of an ordinary differential equation (ODEs), with some functional input that is unknown. Inference of such systems can be difficult, particularly when the dynamics are non-linear and the input is unknown. In this work, we place a Gaussian process (GP) prior over the input function which results in a stochastic It\^o process. Using an autoregressive variational approach, we simulate samples from the resulting process and conform them to the dynamics of the system, conditioned on some observation model. We apply the approach to non-linear ODEs to evaluate the method. As a simulation-based inference method, we also show how it can be extended to models with non-Gaussian likelihoods, such as count data.

Black-Box Autoregressive Density Estimation for State-Space Models

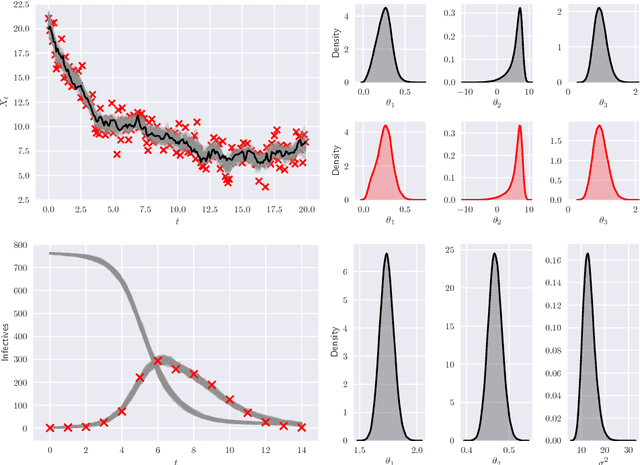
State-space models (SSMs) provide a flexible framework for modelling time-series data. Consequently, SSMs are ubiquitously applied in areas such as engineering, econometrics and epidemiology. In this paper we provide a fast approach for approximate Bayesian inference in SSMs using the tools of deep learning and variational inference.

Black-box Variational Inference for Stochastic Differential Equations

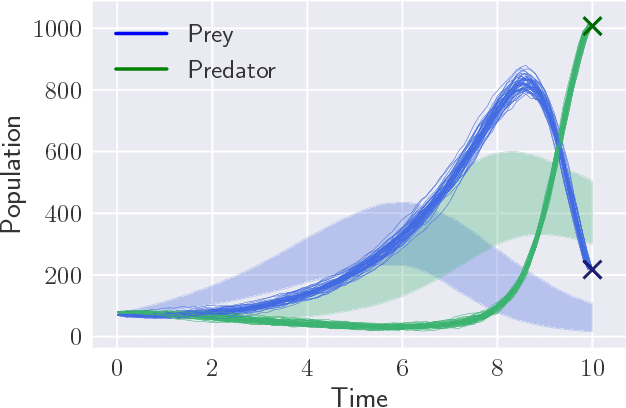
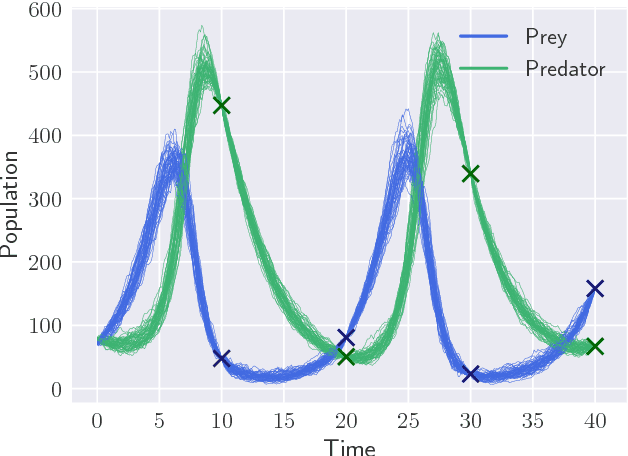
Parameter inference for stochastic differential equations is challenging due to the presence of a latent diffusion process. Working with an Euler-Maruyama discretisation for the diffusion, we use variational inference to jointly learn the parameters and the diffusion paths. We use a standard mean-field variational approximation of the parameter posterior, and introduce a recurrent neural network to approximate the posterior for the diffusion paths conditional on the parameters. This neural network learns how to provide Gaussian state transitions which bridge between observations in a very similar way to the conditioned diffusion process. The resulting black-box inference method can be applied to any SDE system with light tuning requirements. We illustrate the method on a Lotka-Volterra system and an epidemic model, producing accurate parameter estimates in a few hours.

Marginal sequential Monte Carlo for doubly intractable models

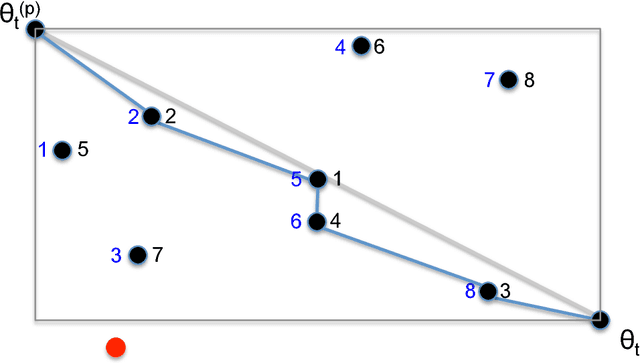
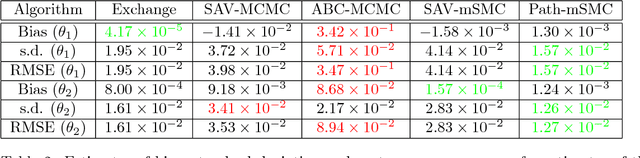
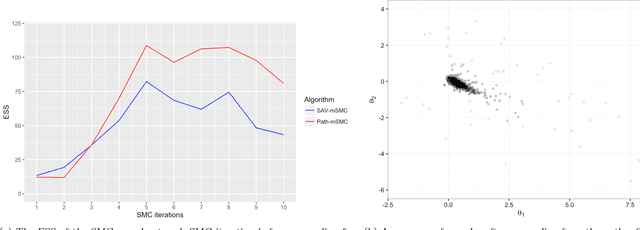
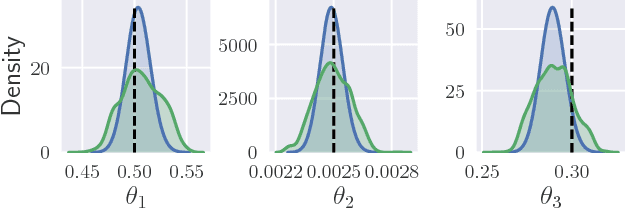
Bayesian inference for models that have an intractable partition function is known as a doubly intractable problem, where standard Monte Carlo methods are not applicable. The past decade has seen the development of auxiliary variable Monte Carlo techniques (M{\o}ller et al., 2006; Murray et al., 2006) for tackling this problem; these approaches being members of the more general class of pseudo-marginal, or exact-approximate, Monte Carlo algorithms (Andrieu and Roberts, 2009), which make use of unbiased estimates of intractable posteriors. Everitt et al. (2017) investigated the use of exact-approximate importance sampling (IS) and sequential Monte Carlo (SMC) in doubly intractable problems, but focussed only on SMC algorithms that used data-point tempering. This paper describes SMC samplers that may use alternative sequences of distributions, and describes ways in which likelihood estimates may be improved adaptively as the algorithm progresses, building on ideas from Moores et al. (2015). This approach is compared with a number of alternative algorithms for doubly intractable problems, including approximate Bayesian computation (ABC), which we show is closely related to the method of M{\o}ller et al. (2006).