ARCHANGEL: Tamper-proofing Video Archives using Temporal Content Hashes on the Blockchain

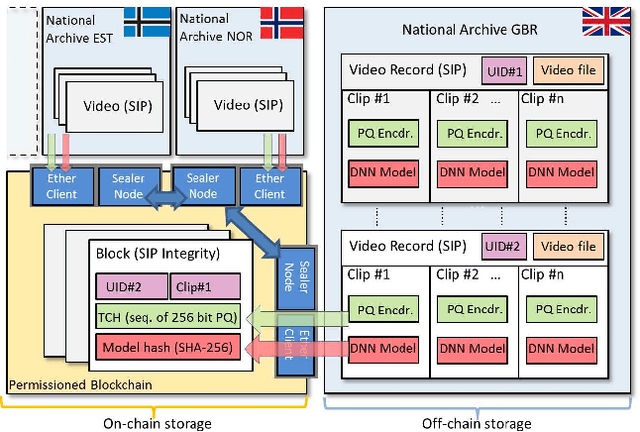
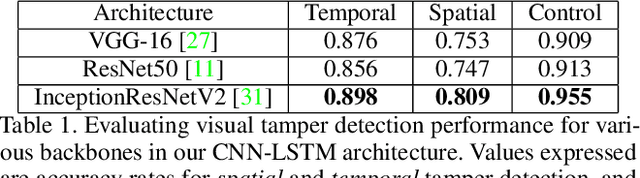
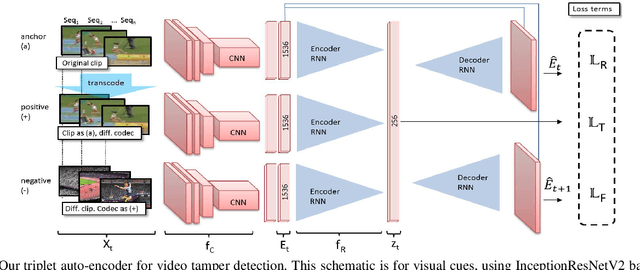
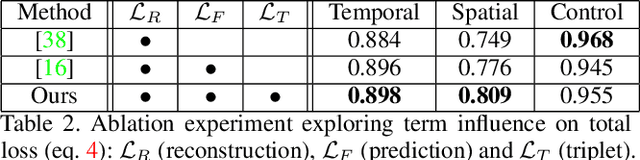
We present ARCHANGEL; a novel distributed ledger based system for assuring the long-term integrity of digital video archives. First, we describe a novel deep network architecture for computing compact temporal content hashes (TCHs) from audio-visual streams with durations of minutes or hours. Our TCHs are sensitive to accidental or malicious content modification (tampering) but invariant to the codec used to encode the video. This is necessary due to the curatorial requirement for archives to format shift video over time to ensure future accessibility. Second, we describe how the TCHs (and the models used to derive them) are secured via a proof-of-authority blockchain distributed across multiple independent archives. We report on the efficacy of ARCHANGEL within the context of a trial deployment in which the national government archives of the United Kingdom, Estonia and Norway participated.

Marginal sequential Monte Carlo for doubly intractable models

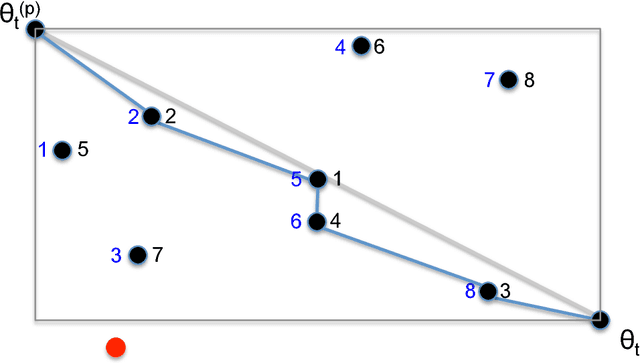
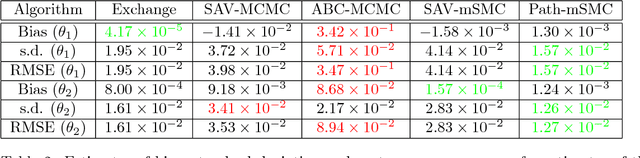
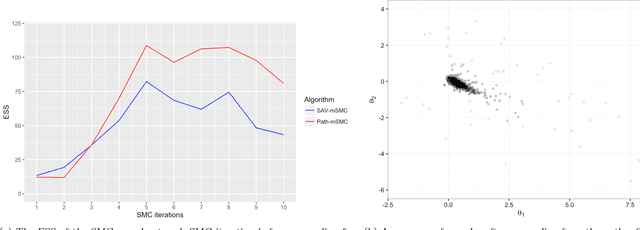
Bayesian inference for models that have an intractable partition function is known as a doubly intractable problem, where standard Monte Carlo methods are not applicable. The past decade has seen the development of auxiliary variable Monte Carlo techniques (M{\o}ller et al., 2006; Murray et al., 2006) for tackling this problem; these approaches being members of the more general class of pseudo-marginal, or exact-approximate, Monte Carlo algorithms (Andrieu and Roberts, 2009), which make use of unbiased estimates of intractable posteriors. Everitt et al. (2017) investigated the use of exact-approximate importance sampling (IS) and sequential Monte Carlo (SMC) in doubly intractable problems, but focussed only on SMC algorithms that used data-point tempering. This paper describes SMC samplers that may use alternative sequences of distributions, and describes ways in which likelihood estimates may be improved adaptively as the algorithm progresses, building on ideas from Moores et al. (2015). This approach is compared with a number of alternative algorithms for doubly intractable problems, including approximate Bayesian computation (ABC), which we show is closely related to the method of M{\o}ller et al. (2006).