Generalized Bayesian deep reinforcement learning

Bayesian reinforcement learning (BRL) is a method that merges principles from Bayesian statistics and reinforcement learning to make optimal decisions in uncertain environments. Similar to other model-based RL approaches, it involves two key components: (1) Inferring the posterior distribution of the data generating process (DGP) modeling the true environment and (2) policy learning using the learned posterior. We propose to model the dynamics of the unknown environment through deep generative models assuming Markov dependence. In absence of likelihood functions for these models we train them by learning a generalized predictive-sequential (or prequential) scoring rule (SR) posterior. We use sequential Monte Carlo (SMC) samplers to draw samples from this generalized Bayesian posterior distribution. In conjunction, to achieve scalability in the high dimensional parameter space of the neural networks, we use the gradient based Markov chain Monte Carlo (MCMC) kernels within SMC. To justify the use of the prequential scoring rule posterior we prove a Bernstein-von Misses type theorem. For policy learning, we propose expected Thompson sampling (ETS) to learn the optimal policy by maximizing the expected value function with respect to the posterior distribution. This improves upon traditional Thompson sampling (TS) and its extensions which utilize only one sample drawn from the posterior distribution. This improvement is studied both theoretically and using simulation studies assuming discrete action and state-space. Finally we successfully extend our setup for a challenging problem with continuous action space without theoretical guarantees.

Bootstrapped synthetic likelihood

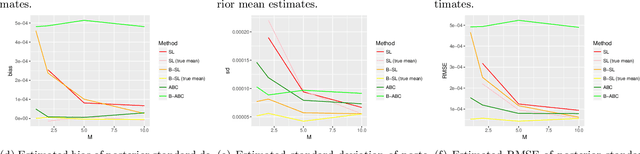
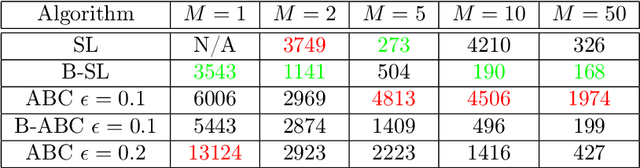
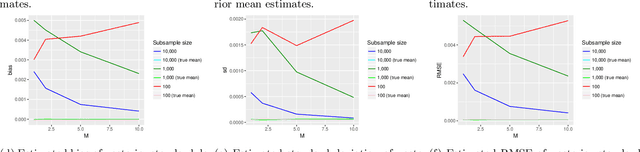
Approximate Bayesian computation (ABC) and synthetic likelihood (SL) techniques have enabled the use of Bayesian inference for models that may be simulated, but for which the likelihood cannot be evaluated pointwise at values of an unknown parameter $\theta$. The main idea in ABC and SL is to, for different values of $\theta$ (usually chosen using a Monte Carlo algorithm), build estimates of the likelihood based on simulations from the model conditional on $\theta$. The quality of these estimates determines the efficiency of an ABC/SL algorithm. In standard ABC/SL, the only means to improve an estimated likelihood at $\theta$ is to simulate more times from the model conditional on $\theta$, which is infeasible in cases where the simulator is computationally expensive. In this paper we describe how to use bootstrapping as a means for improving SL estimates whilst using fewer simulations from the model, and also investigate its use in ABC. Further, we investigate the use of the bag of little bootstraps as a means for applying this approach to large datasets, yielding Monte Carlo algorithms that accurately approximate posterior distributions whilst only simulating subsamples of the full data. Examples of the approach applied to i.i.d., temporal and spatial data are given.

Marginal sequential Monte Carlo for doubly intractable models

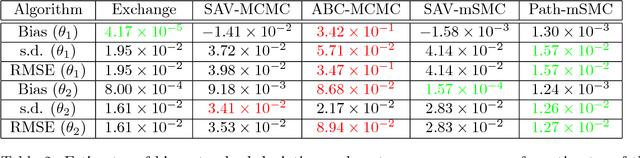
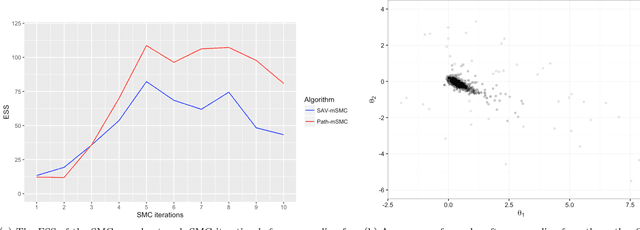
Bayesian inference for models that have an intractable partition function is known as a doubly intractable problem, where standard Monte Carlo methods are not applicable. The past decade has seen the development of auxiliary variable Monte Carlo techniques (M{\o}ller et al., 2006; Murray et al., 2006) for tackling this problem; these approaches being members of the more general class of pseudo-marginal, or exact-approximate, Monte Carlo algorithms (Andrieu and Roberts, 2009), which make use of unbiased estimates of intractable posteriors. Everitt et al. (2017) investigated the use of exact-approximate importance sampling (IS) and sequential Monte Carlo (SMC) in doubly intractable problems, but focussed only on SMC algorithms that used data-point tempering. This paper describes SMC samplers that may use alternative sequences of distributions, and describes ways in which likelihood estimates may be improved adaptively as the algorithm progresses, building on ideas from Moores et al. (2015). This approach is compared with a number of alternative algorithms for doubly intractable problems, including approximate Bayesian computation (ABC), which we show is closely related to the method of M{\o}ller et al. (2006).

Delayed acceptance ABC-SMC

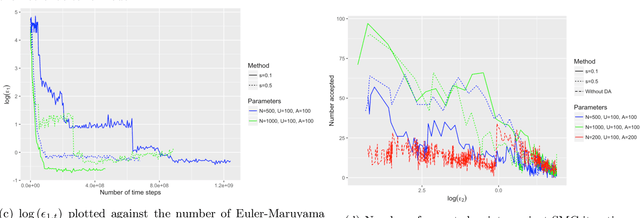
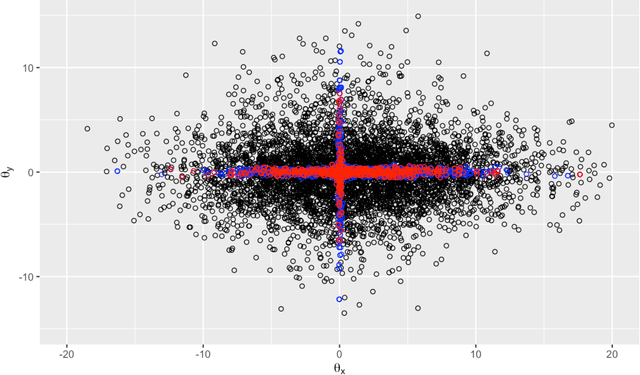
Approximate Bayesian computation (ABC) is now an established technique for statistical inference used in cases where the likelihood function is computationally expensive or not available. It relies on the use of a model that is specified in the form of a simulator, and approximates the likelihood at a parameter $\theta$ by simulating auxiliary data sets $x$ and evaluating the distance of $x$ from the true data $y$. However, ABC is not computationally feasible in cases where using the simulator for each $\theta$ is very expensive. This paper investigates this situation in cases where a cheap, but approximate, simulator is available. The approach is to employ delayed acceptance Markov chain Monte Carlo (MCMC) within an ABC sequential Monte Carlo (SMC) sampler in order to, in a first stage of the kernel, use the cheap simulator to rule out parts of the parameter space that are not worth exploring, so that the "true" simulator is only run (in the second stage of the kernel) where there is a reasonable chance of accepting proposed values of $\theta$. We show that this approach can be used quite automatically, with the only tuning parameter choice additional to ABC-SMC being the number of particles we wish to carry through to the second stage of the kernel. Applications to stochastic differential equation models and latent doubly intractable distributions are presented.

An ABC interpretation of the multiple auxiliary variable method

We show that the auxiliary variable method (M{\o}ller et al., 2006; Murray et al., 2006) for inference of Markov random fields can be viewed as an approximate Bayesian computation method for likelihood estimation.

Bayesian model comparison with un-normalised likelihoods

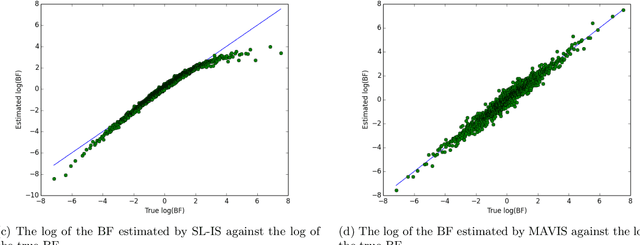
Models for which the likelihood function can be evaluated only up to a parameter-dependent unknown normalising constant, such as Markov random field models, are used widely in computer science, statistical physics, spatial statistics, and network analysis. However, Bayesian analysis of these models using standard Monte Carlo methods is not possible due to the intractability of their likelihood functions. Several methods that permit exact, or close to exact, simulation from the posterior distribution have recently been developed. However, estimating the evidence and Bayes' factors (BFs) for these models remains challenging in general. This paper describes new random weight importance sampling and sequential Monte Carlo methods for estimating BFs that use simulation to circumvent the evaluation of the intractable likelihood, and compares them to existing methods. In some cases we observe an advantage in the use of biased weight estimates. An initial investigation into the theoretical and empirical properties of this class of methods is presented. Some support for the use of biased estimates is presented, but we advocate caution in the use of such estimates.

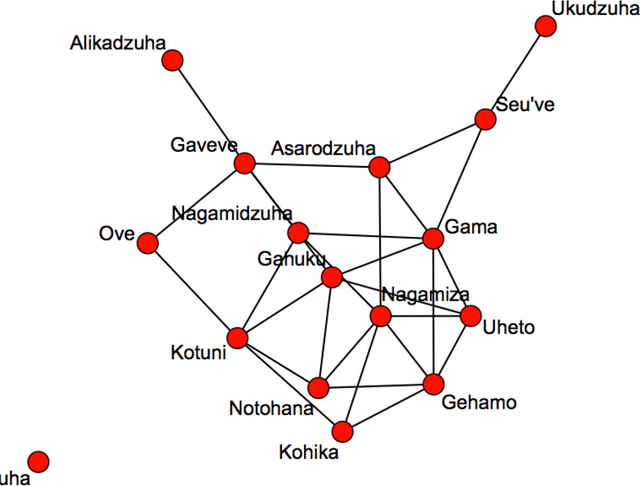
Bayesian Parameter Estimation for Latent Markov Random Fields and Social Networks

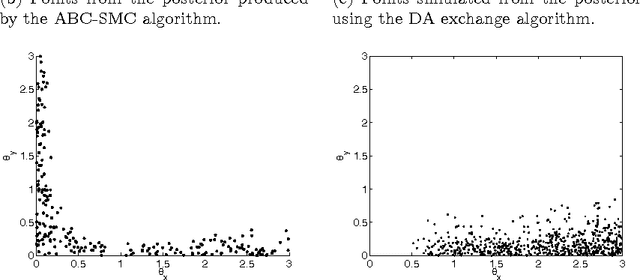
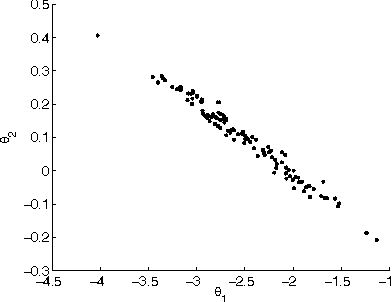
Undirected graphical models are widely used in statistics, physics and machine vision. However Bayesian parameter estimation for undirected models is extremely challenging, since evaluation of the posterior typically involves the calculation of an intractable normalising constant. This problem has received much attention, but very little of this has focussed on the important practical case where the data consists of noisy or incomplete observations of the underlying hidden structure. This paper specifically addresses this problem, comparing two alternative methodologies. In the first of these approaches particle Markov chain Monte Carlo (Andrieu et al., 2010) is used to efficiently explore the parameter space, combined with the exchange algorithm (Murray et al., 2006) for avoiding the calculation of the intractable normalising constant (a proof showing that this combination targets the correct distribution in found in a supplementary appendix online). This approach is compared with approximate Bayesian computation (Pritchard et al., 1999). Applications to estimating the parameters of Ising models and exponential random graphs from noisy data are presented. Each algorithm used in the paper targets an approximation to the true posterior due to the use of MCMC to simulate from the latent graphical model, in lieu of being able to do this exactly in general. The supplementary appendix also describes the nature of the resulting approximation.