Generalized Bayesian deep reinforcement learning

Bayesian reinforcement learning (BRL) is a method that merges principles from Bayesian statistics and reinforcement learning to make optimal decisions in uncertain environments. Similar to other model-based RL approaches, it involves two key components: (1) Inferring the posterior distribution of the data generating process (DGP) modeling the true environment and (2) policy learning using the learned posterior. We propose to model the dynamics of the unknown environment through deep generative models assuming Markov dependence. In absence of likelihood functions for these models we train them by learning a generalized predictive-sequential (or prequential) scoring rule (SR) posterior. We use sequential Monte Carlo (SMC) samplers to draw samples from this generalized Bayesian posterior distribution. In conjunction, to achieve scalability in the high dimensional parameter space of the neural networks, we use the gradient based Markov chain Monte Carlo (MCMC) kernels within SMC. To justify the use of the prequential scoring rule posterior we prove a Bernstein-von Misses type theorem. For policy learning, we propose expected Thompson sampling (ETS) to learn the optimal policy by maximizing the expected value function with respect to the posterior distribution. This improves upon traditional Thompson sampling (TS) and its extensions which utilize only one sample drawn from the posterior distribution. This improvement is studied both theoretically and using simulation studies assuming discrete action and state-space. Finally we successfully extend our setup for a challenging problem with continuous action space without theoretical guarantees.

Parallelising MCMC via Random Forests

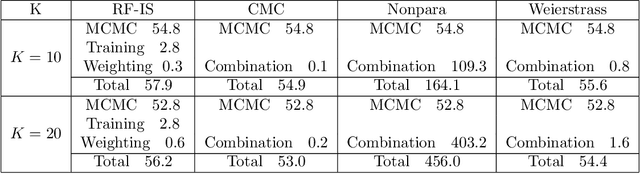
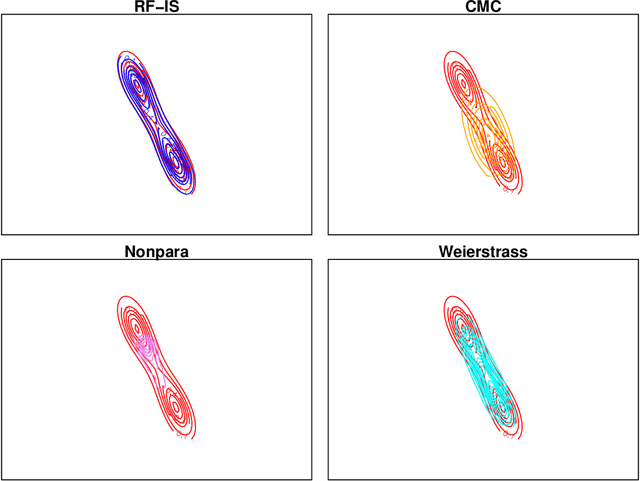
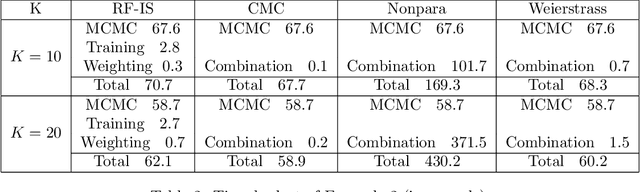
For Bayesian computation in big data contexts, the divide-and-conquer MCMC concept splits the whole data set into batches, runs MCMC algorithms separately over each batch to produce samples of parameters, and combines them to produce an approximation of the target distribution. In this article, we embed random forests into this framework and use each subposterior/partial-posterior as a proposal distribution to implement importance sampling. Unlike the existing divide-and-conquer MCMC, our methods are based on scaled subposteriors, whose scale factors are not necessarily restricted to being equal to one or to the number of subsets. Through several experiments, we show that our methods work well with models ranging from Gaussian cases to strongly non-Gaussian cases, and include model misspecification.

ABC random forests for Bayesian parameter inference

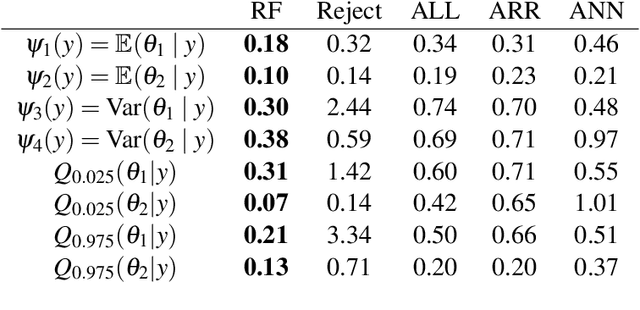
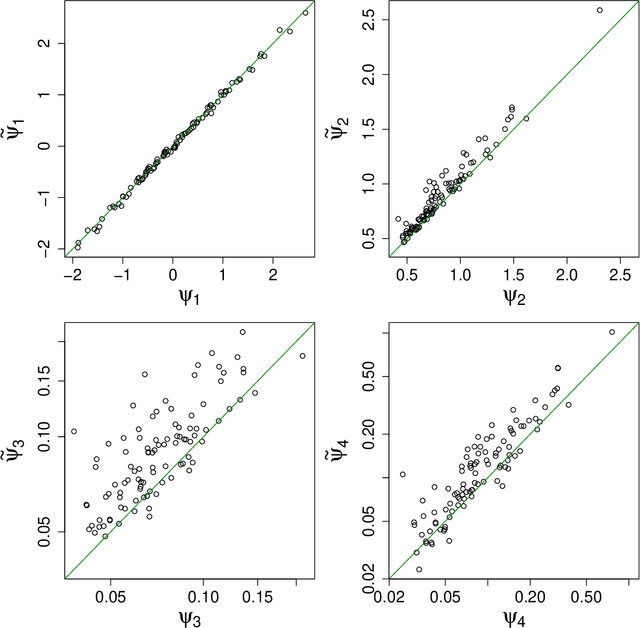
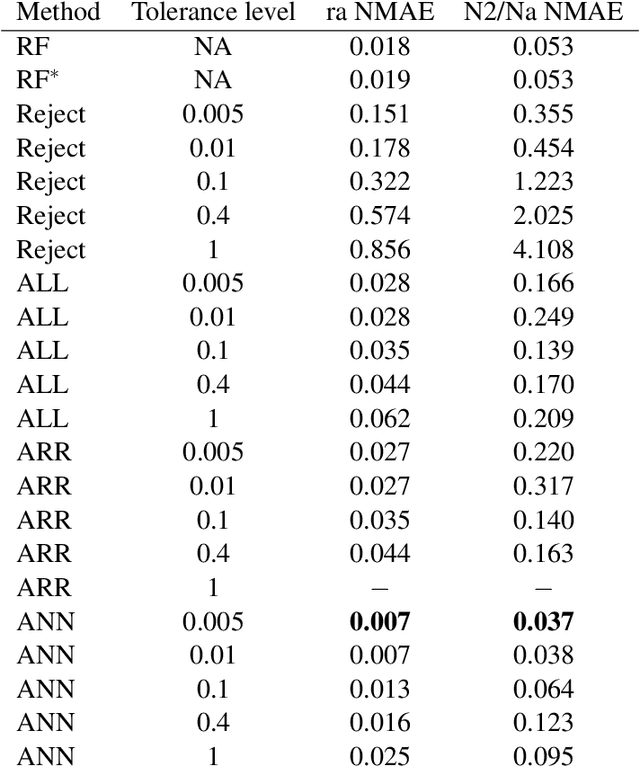
This preprint has been reviewed and recommended by Peer Community In Evolutionary Biology (http://dx.doi.org/10.24072/pci.evolbiol.100036). Approximate Bayesian computation (ABC) has grown into a standard methodology that manages Bayesian inference for models associated with intractable likelihood functions. Most ABC implementations require the preliminary selection of a vector of informative statistics summarizing raw data. Furthermore, in almost all existing implementations, the tolerance level that separates acceptance from rejection of simulated parameter values needs to be calibrated. We propose to conduct likelihood-free Bayesian inferences about parameters with no prior selection of the relevant components of the summary statistics and bypassing the derivation of the associated tolerance level. The approach relies on the random forest methodology of Breiman (2001) applied in a (non parametric) regression setting. We advocate the derivation of a new random forest for each component of the parameter vector of interest. When compared with earlier ABC solutions, this method offers significant gains in terms of robustness to the choice of the summary statistics, does not depend on any type of tolerance level, and is a good trade-off in term of quality of point estimator precision and credible interval estimations for a given computing time. We illustrate the performance of our methodological proposal and compare it with earlier ABC methods on a Normal toy example and a population genetics example dealing with human population evolution. All methods designed here have been incorporated in the R package abcrf (version 1.7) available on CRAN.

Likelihood-free Model Choice

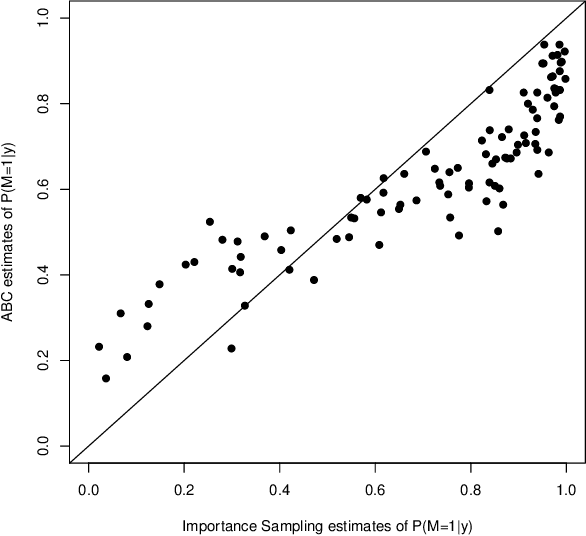
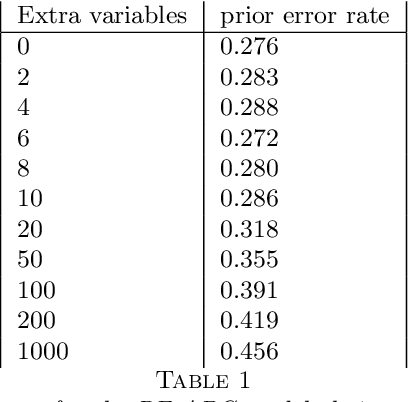
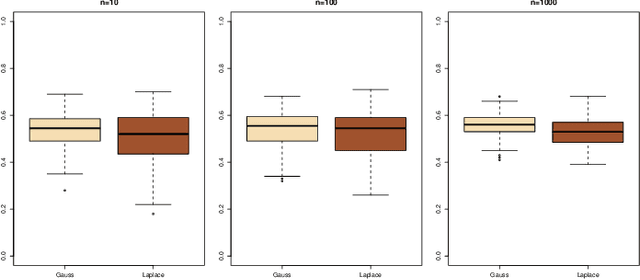
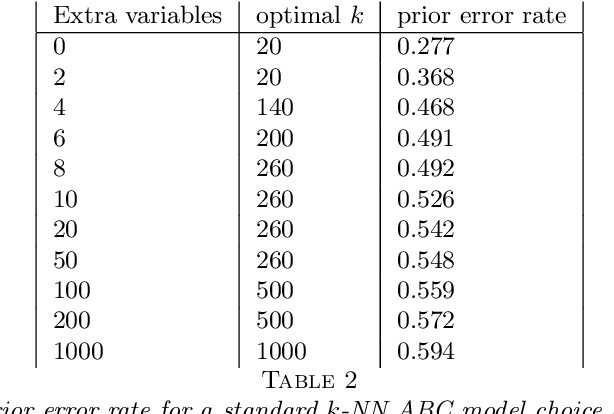
This document is an invited chapter covering the specificities of ABC model choice, intended for the incoming Handbook of ABC by Sisson, Fan, and Beaumont (2017). Beyond exposing the potential pitfalls of ABC based posterior probabilities, the review emphasizes mostly the solution proposed by Pudlo et al. (2016) on the use of random forests for aggregating summary statistics and and for estimating the posterior probability of the most likely model via a secondary random fores.

Reliable ABC model choice via random forests

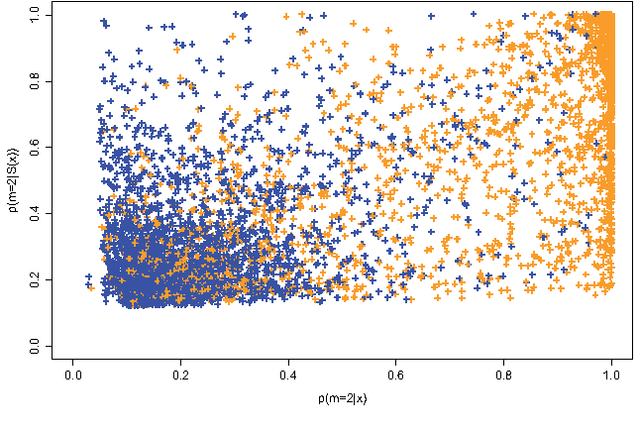
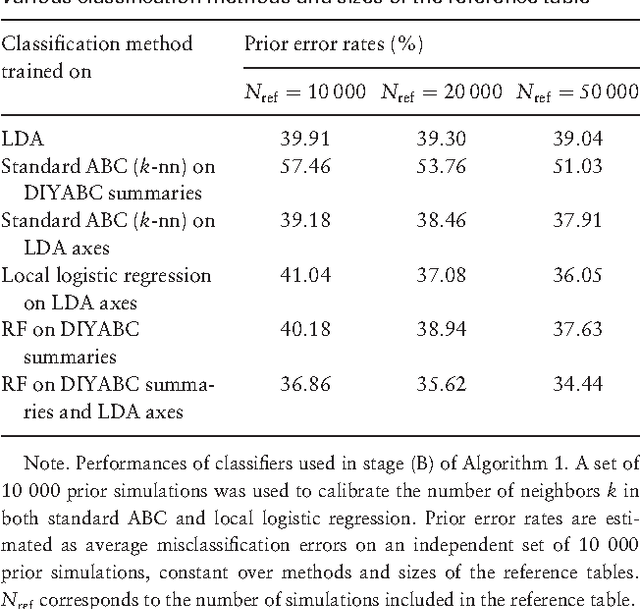
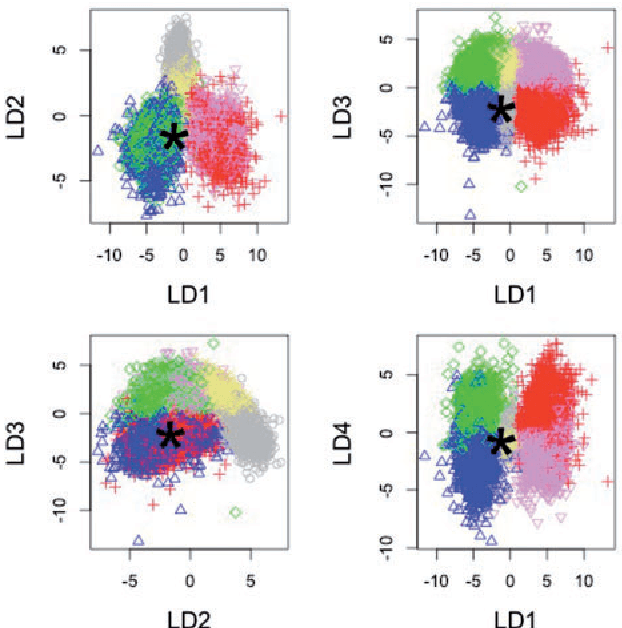
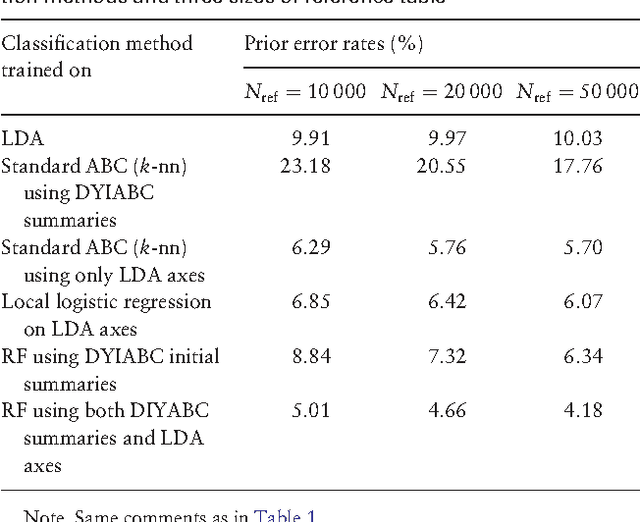
Approximate Bayesian computation (ABC) methods provide an elaborate approach to Bayesian inference on complex models, including model choice. Both theoretical arguments and simulation experiments indicate, however, that model posterior probabilities may be poorly evaluated by standard ABC techniques. We propose a novel approach based on a machine learning tool named random forests to conduct selection among the highly complex models covered by ABC algorithms. We thus modify the way Bayesian model selection is both understood and operated, in that we rephrase the inferential goal as a classification problem, first predicting the model that best fits the data with random forests and postponing the approximation of the posterior probability of the predicted MAP for a second stage also relying on random forests. Compared with earlier implementations of ABC model choice, the ABC random forest approach offers several potential improvements: (i) it often has a larger discriminative power among the competing models, (ii) it is more robust against the number and choice of statistics summarizing the data, (iii) the computing effort is drastically reduced (with a gain in computation efficiency of at least fifty), and (iv) it includes an approximation of the posterior probability of the selected model. The call to random forests will undoubtedly extend the range of size of datasets and complexity of models that ABC can handle. We illustrate the power of this novel methodology by analyzing controlled experiments as well as genuine population genetics datasets. The proposed methodologies are implemented in the R package abcrf available on the CRAN.