Selection of Summary Statistics for Network Model Choice with Approximate Bayesian Computation

Approximate Bayesian Computation (ABC) now serves as one of the major strategies to perform model choice and parameter inference on models with intractable likelihoods. An essential component of ABC involves comparing a large amount of simulated data with the observed data through summary statistics. To avoid the curse of dimensionality, summary statistic selection is of prime importance, and becomes even more critical when applying ABC to mechanistic network models. Indeed, while many summary statistics can be used to encode network structures, their computational complexity can be highly variable. For large networks, computation of summary statistics can quickly create a bottleneck, making the use of ABC difficult. To reduce this computational burden and make the analysis of mechanistic network models more practical, we investigated two questions in a model choice framework. First, we studied the utility of cost-based filter selection methods to account for different summary costs during the selection process. Second, we performed selection using networks generated with a smaller number of nodes to reduce the time required for the selection step. Our findings show that computationally inexpensive summary statistics can be efficiently selected with minimal impact on classification accuracy. Furthermore, we found that networks with a smaller number of nodes can only be employed to eliminate a moderate number of summaries. While this latter finding is network specific, the former is general and can be adapted to any ABC application.

ABC random forests for Bayesian parameter inference

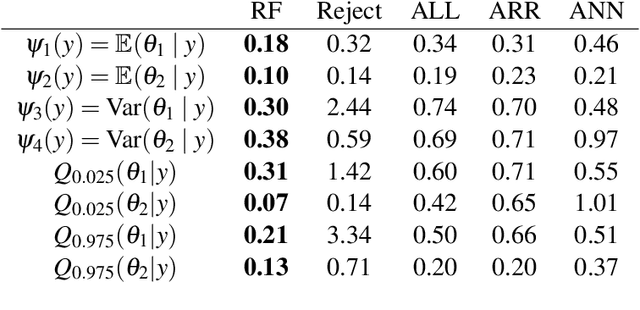
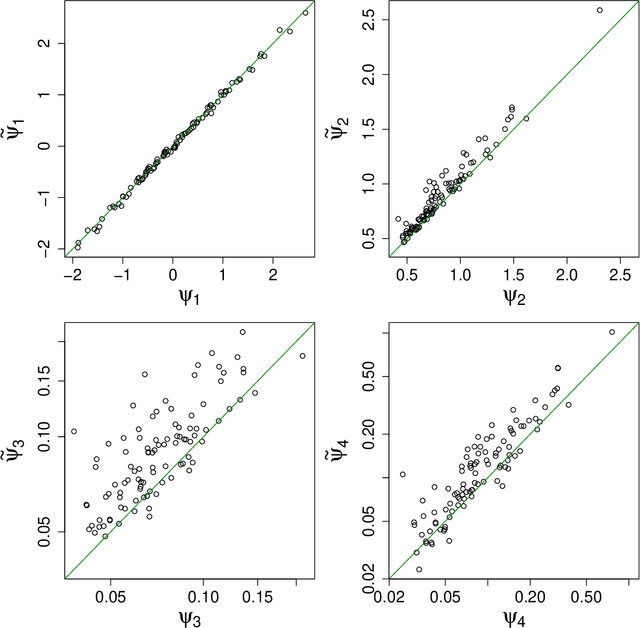
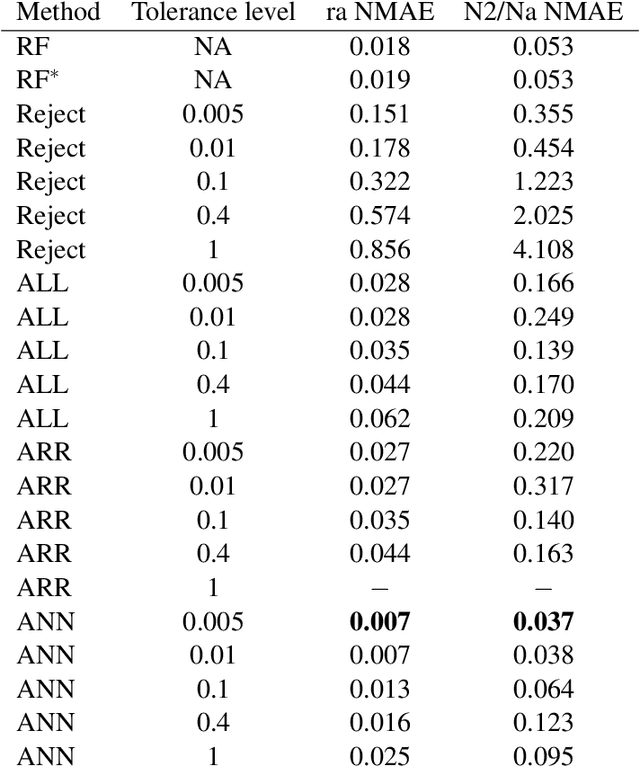
This preprint has been reviewed and recommended by Peer Community In Evolutionary Biology (http://dx.doi.org/10.24072/pci.evolbiol.100036). Approximate Bayesian computation (ABC) has grown into a standard methodology that manages Bayesian inference for models associated with intractable likelihood functions. Most ABC implementations require the preliminary selection of a vector of informative statistics summarizing raw data. Furthermore, in almost all existing implementations, the tolerance level that separates acceptance from rejection of simulated parameter values needs to be calibrated. We propose to conduct likelihood-free Bayesian inferences about parameters with no prior selection of the relevant components of the summary statistics and bypassing the derivation of the associated tolerance level. The approach relies on the random forest methodology of Breiman (2001) applied in a (non parametric) regression setting. We advocate the derivation of a new random forest for each component of the parameter vector of interest. When compared with earlier ABC solutions, this method offers significant gains in terms of robustness to the choice of the summary statistics, does not depend on any type of tolerance level, and is a good trade-off in term of quality of point estimator precision and credible interval estimations for a given computing time. We illustrate the performance of our methodological proposal and compare it with earlier ABC methods on a Normal toy example and a population genetics example dealing with human population evolution. All methods designed here have been incorporated in the R package abcrf (version 1.7) available on CRAN.