Dirichlet process mixture model based on topologically augmented signal representation for clustering infant vocalizations

Based on audio recordings made once a month during the first 12 months of a child's life, we propose a new method for clustering this set of vocalizations. We use a topologically augmented representation of the vocalizations, employing two persistence diagrams for each vocalization: one computed on the surface of its spectrogram and one on the Takens' embeddings of the vocalization. A synthetic persistent variable is derived for each diagram and added to the MFCCs (Mel-frequency cepstral coefficients). Using this representation, we fit a non-parametric Bayesian mixture model with a Dirichlet process prior to model the number of components. This procedure leads to a novel data-driven categorization of vocal productions. Our findings reveal the presence of 8 clusters of vocalizations, allowing us to compare their temporal distribution and acoustic profiles in the first 12 months of life.

Topological data analysis of human vowels: Persistent homologies across representation spaces

Topological Data Analysis (TDA) has been successfully used for various tasks in signal/image processing, from visualization to supervised/unsupervised classification. Often, topological characteristics are obtained from persistent homology theory. The standard TDA pipeline starts from the raw signal data or a representation of it. Then, it consists in building a multiscale topological structure on the top of the data using a pre-specified filtration, and finally to compute the topological signature to be further exploited. The commonly used topological signature is a persistent diagram (or transformations of it). Current research discusses the consequences of the many ways to exploit topological signatures, much less often the choice of the filtration, but to the best of our knowledge, the choice of the representation of a signal has not been the subject of any study yet. This paper attempts to provide some answers on the latter problem. To this end, we collected real audio data and built a comparative study to assess the quality of the discriminant information of the topological signatures extracted from three different representation spaces. Each audio signal is represented as i) an embedding of observed data in a higher dimensional space using Taken's representation, ii) a spectrogram viewed as a surface in a 3D ambient space, iii) the set of spectrogram's zeroes. From vowel audio recordings, we use topological signature for three prediction problems: speaker gender, vowel type, and individual. We show that topologically-augmented random forest improves the Out-of-Bag Error (OOB) over solely based Mel-Frequency Cepstral Coefficients (MFCC) for the last two problems. Our results also suggest that the topological information extracted from different signal representations is complementary, and that spectrogram's zeros offers the best improvement for gender prediction.

Detecting human and non-human vocal productions in large scale audio recordings

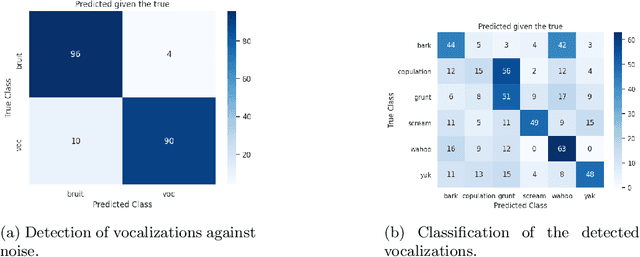
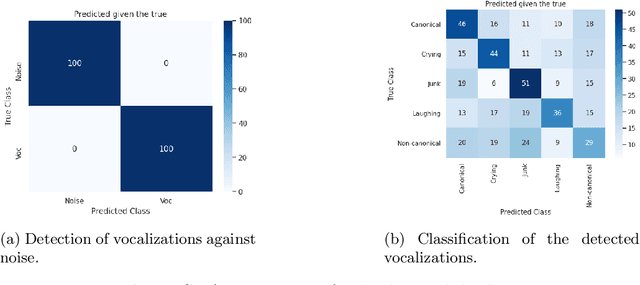
We propose an automatic data processing pipeline to extract vocal productions from large-scale natural audio recordings. Through a series of computational steps (windowing, creation of a noise class, data augmentation, re-sampling, transfer learning, Bayesian optimisation), it automatically trains a neural network for detecting various types of natural vocal productions in a noisy data stream without requiring a large sample of labeled data. We test it on two different data sets, one from a group of Guinea baboons recorded from a primate research center and one from human babies recorded at home. The pipeline trains a model on 72 and 77 minutes of labeled audio recordings, with an accuracy of 94.58% and 99.76%. It is then used to process 443 and 174 hours of natural continuous recordings and it creates two new databases of 38.8 and 35.2 hours, respectively. We discuss the strengths and limitations of this approach that can be applied to any massive audio recording.

ABC random forests for Bayesian parameter inference

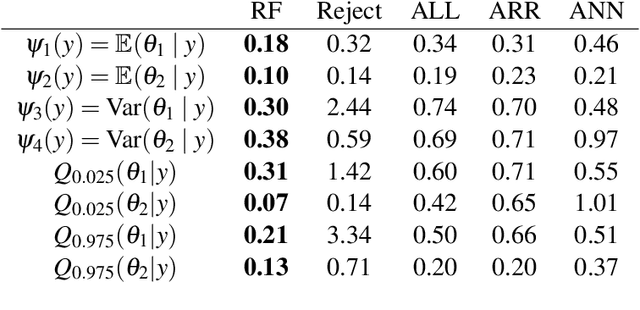
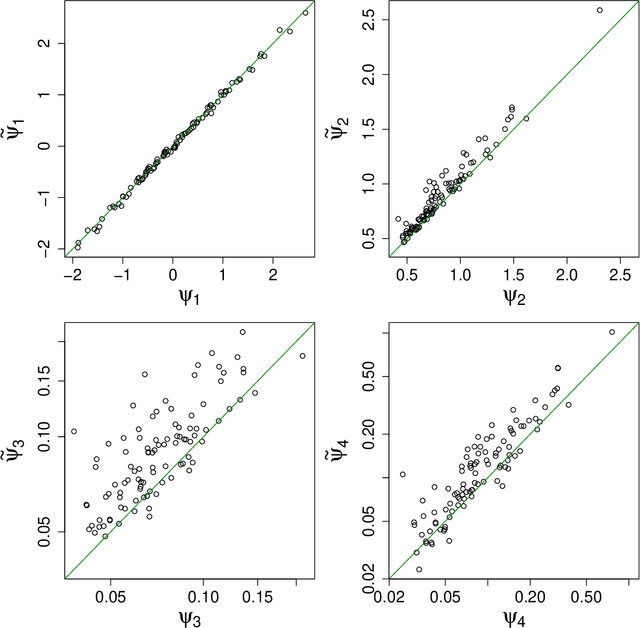
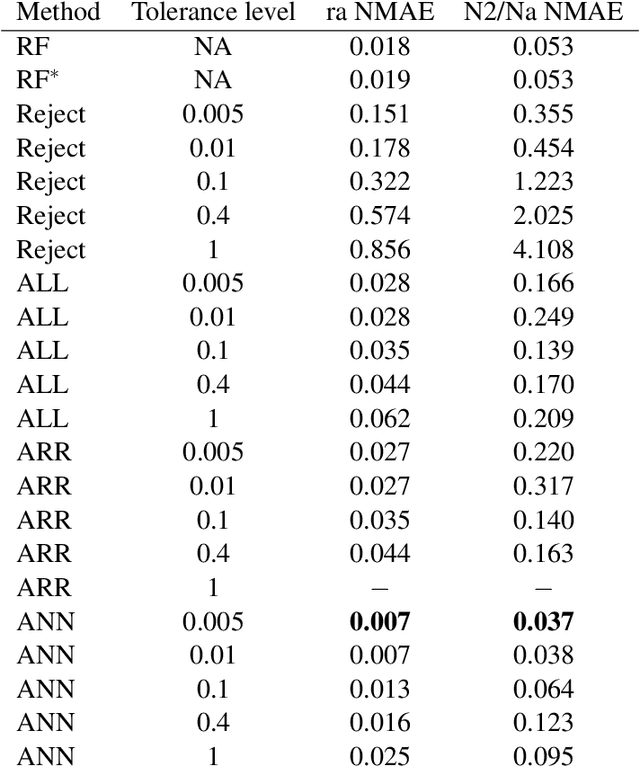
This preprint has been reviewed and recommended by Peer Community In Evolutionary Biology (http://dx.doi.org/10.24072/pci.evolbiol.100036). Approximate Bayesian computation (ABC) has grown into a standard methodology that manages Bayesian inference for models associated with intractable likelihood functions. Most ABC implementations require the preliminary selection of a vector of informative statistics summarizing raw data. Furthermore, in almost all existing implementations, the tolerance level that separates acceptance from rejection of simulated parameter values needs to be calibrated. We propose to conduct likelihood-free Bayesian inferences about parameters with no prior selection of the relevant components of the summary statistics and bypassing the derivation of the associated tolerance level. The approach relies on the random forest methodology of Breiman (2001) applied in a (non parametric) regression setting. We advocate the derivation of a new random forest for each component of the parameter vector of interest. When compared with earlier ABC solutions, this method offers significant gains in terms of robustness to the choice of the summary statistics, does not depend on any type of tolerance level, and is a good trade-off in term of quality of point estimator precision and credible interval estimations for a given computing time. We illustrate the performance of our methodological proposal and compare it with earlier ABC methods on a Normal toy example and a population genetics example dealing with human population evolution. All methods designed here have been incorporated in the R package abcrf (version 1.7) available on CRAN.

Likelihood-free Model Choice

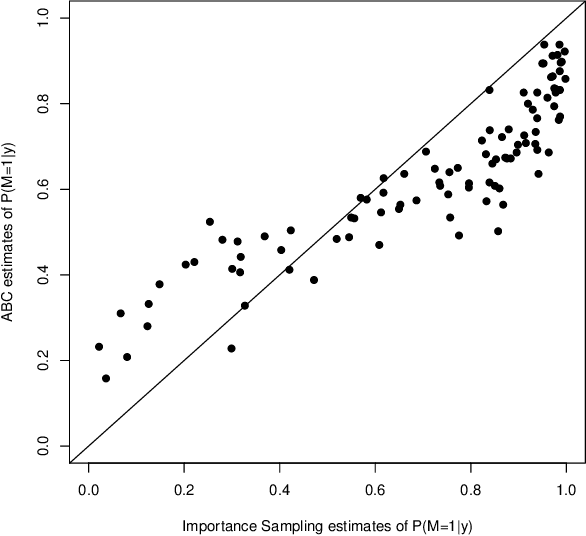
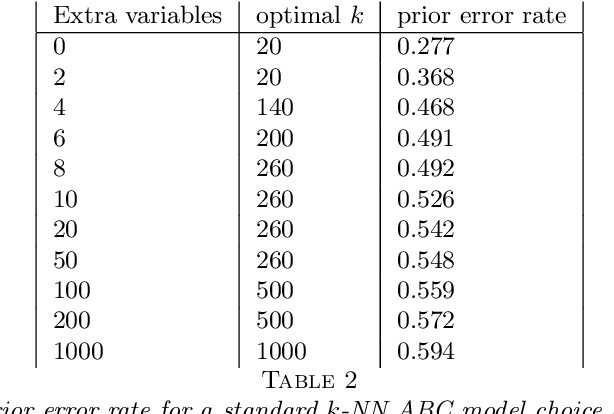
This document is an invited chapter covering the specificities of ABC model choice, intended for the incoming Handbook of ABC by Sisson, Fan, and Beaumont (2017). Beyond exposing the potential pitfalls of ABC based posterior probabilities, the review emphasizes mostly the solution proposed by Pudlo et al. (2016) on the use of random forests for aggregating summary statistics and and for estimating the posterior probability of the most likely model via a secondary random fores.

Reliable ABC model choice via random forests

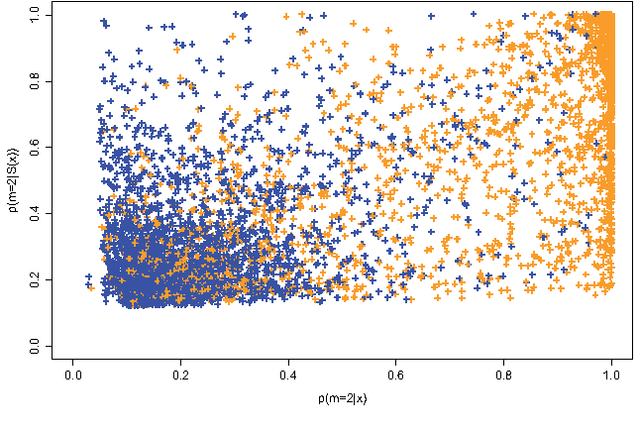
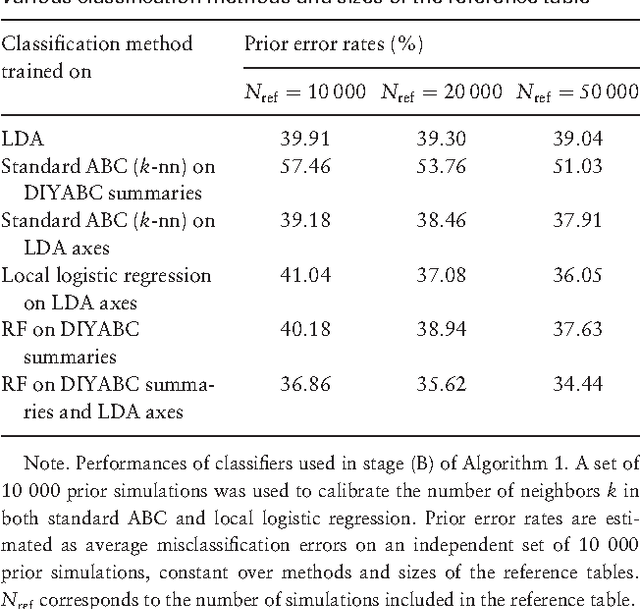
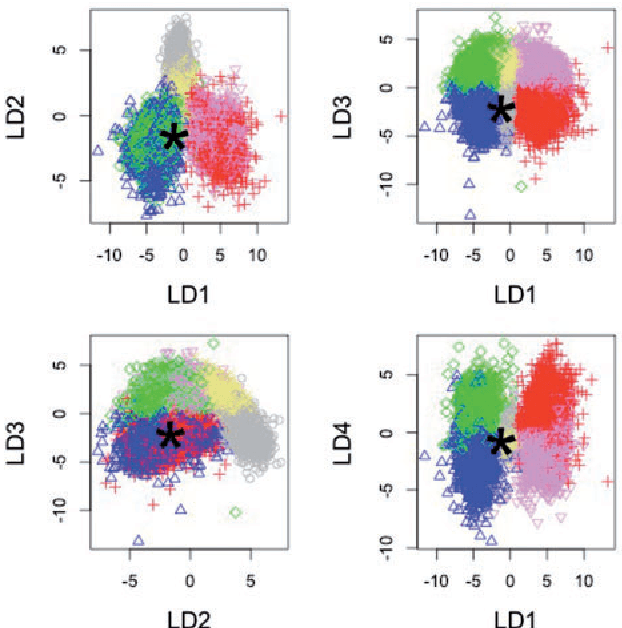
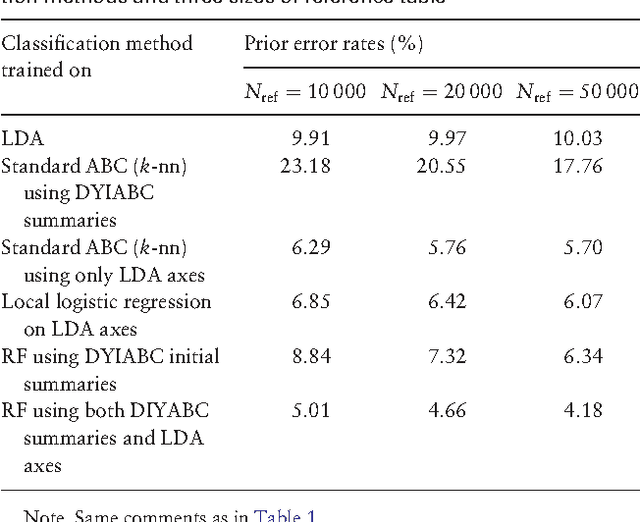
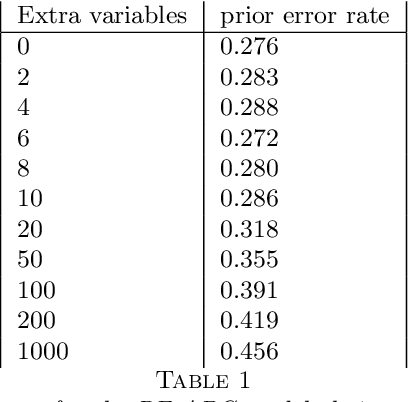
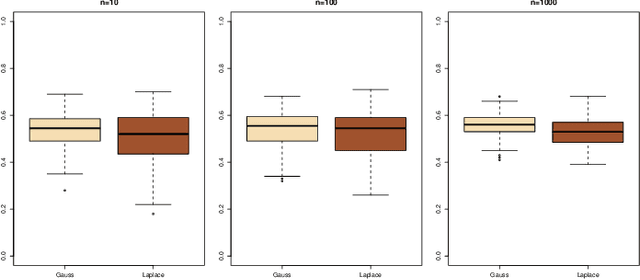
Approximate Bayesian computation (ABC) methods provide an elaborate approach to Bayesian inference on complex models, including model choice. Both theoretical arguments and simulation experiments indicate, however, that model posterior probabilities may be poorly evaluated by standard ABC techniques. We propose a novel approach based on a machine learning tool named random forests to conduct selection among the highly complex models covered by ABC algorithms. We thus modify the way Bayesian model selection is both understood and operated, in that we rephrase the inferential goal as a classification problem, first predicting the model that best fits the data with random forests and postponing the approximation of the posterior probability of the predicted MAP for a second stage also relying on random forests. Compared with earlier implementations of ABC model choice, the ABC random forest approach offers several potential improvements: (i) it often has a larger discriminative power among the competing models, (ii) it is more robust against the number and choice of statistics summarizing the data, (iii) the computing effort is drastically reduced (with a gain in computation efficiency of at least fifty), and (iv) it includes an approximation of the posterior probability of the selected model. The call to random forests will undoubtedly extend the range of size of datasets and complexity of models that ABC can handle. We illustrate the power of this novel methodology by analyzing controlled experiments as well as genuine population genetics datasets. The proposed methodologies are implemented in the R package abcrf available on the CRAN.

Operator norm convergence of spectral clustering on level sets

Following Hartigan, a cluster is defined as a connected component of the t-level set of the underlying density, i.e., the set of points for which the density is greater than t. A clustering algorithm which combines a density estimate with spectral clustering techniques is proposed. Our algorithm is composed of two steps. First, a nonparametric density estimate is used to extract the data points for which the estimated density takes a value greater than t. Next, the extracted points are clustered based on the eigenvectors of a graph Laplacian matrix. Under mild assumptions, we prove the almost sure convergence in operator norm of the empirical graph Laplacian operator associated with the algorithm. Furthermore, we give the typical behavior of the representation of the dataset into the feature space, which establishes the strong consistency of our proposed algorithm.