Generalized Bayesian deep reinforcement learning

Bayesian reinforcement learning (BRL) is a method that merges principles from Bayesian statistics and reinforcement learning to make optimal decisions in uncertain environments. Similar to other model-based RL approaches, it involves two key components: (1) Inferring the posterior distribution of the data generating process (DGP) modeling the true environment and (2) policy learning using the learned posterior. We propose to model the dynamics of the unknown environment through deep generative models assuming Markov dependence. In absence of likelihood functions for these models we train them by learning a generalized predictive-sequential (or prequential) scoring rule (SR) posterior. We use sequential Monte Carlo (SMC) samplers to draw samples from this generalized Bayesian posterior distribution. In conjunction, to achieve scalability in the high dimensional parameter space of the neural networks, we use the gradient based Markov chain Monte Carlo (MCMC) kernels within SMC. To justify the use of the prequential scoring rule posterior we prove a Bernstein-von Misses type theorem. For policy learning, we propose expected Thompson sampling (ETS) to learn the optimal policy by maximizing the expected value function with respect to the posterior distribution. This improves upon traditional Thompson sampling (TS) and its extensions which utilize only one sample drawn from the posterior distribution. This improvement is studied both theoretically and using simulation studies assuming discrete action and state-space. Finally we successfully extend our setup for a challenging problem with continuous action space without theoretical guarantees.

Your copula is a classifier in disguise: classification-based copula density estimation

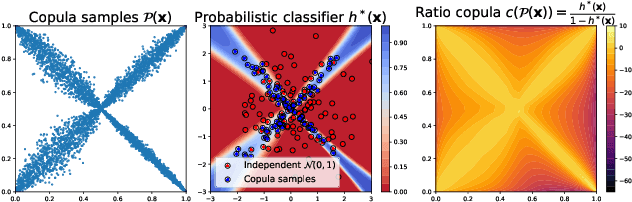
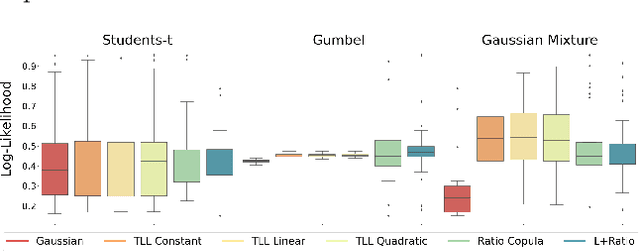
We propose reinterpreting copula density estimation as a discriminative task. Under this novel estimation scheme, we train a classifier to distinguish samples from the joint density from those of the product of independent marginals, recovering the copula density in the process. We derive equivalences between well-known copula classes and classification problems naturally arising in our interpretation. Furthermore, we show our estimator achieves theoretical guarantees akin to maximum likelihood estimation. By identifying a connection with density ratio estimation, we benefit from the rich literature and models available for such problems. Empirically, we demonstrate the applicability of our approach by estimating copulas of real and high-dimensional datasets, outperforming competing copula estimators in density evaluation as well as sampling.

Quasi-Bayes meets Vines

Recently proposed quasi-Bayesian (QB) methods initiated a new era in Bayesian computation by directly constructing the Bayesian predictive distribution through recursion, removing the need for expensive computations involved in sampling the Bayesian posterior distribution. This has proved to be data-efficient for univariate predictions, but extensions to multiple dimensions rely on a conditional decomposition resulting from predefined assumptions on the kernel of the Dirichlet Process Mixture Model, which is the implicit nonparametric model used. Here, we propose a different way to extend Quasi-Bayesian prediction to high dimensions through the use of Sklar's theorem by decomposing the predictive distribution into one-dimensional predictive marginals and a high-dimensional copula. Thus, we use the efficient recursive QB construction for the one-dimensional marginals and model the dependence using highly expressive vine copulas. Further, we tune hyperparameters using robust divergences (eg. energy score) and show that our proposed Quasi-Bayesian Vine (QB-Vine) is a fully non-parametric density estimator with \emph{an analytical form} and convergence rate independent of the dimension of data in some situations. Our experiments illustrate that the QB-Vine is appropriate for high dimensional distributions ($\sim$64), needs very few samples to train ($\sim$200) and outperforms state-of-the-art methods with analytical forms for density estimation and supervised tasks by a considerable margin.

Likelihood-Free Inference with Generative Neural Networks via Scoring Rule Minimization

Bayesian Likelihood-Free Inference methods yield posterior approximations for simulator models with intractable likelihood. Recently, many works trained neural networks to approximate either the intractable likelihood or the posterior directly. Most proposals use normalizing flows, namely neural networks parametrizing invertible maps used to transform samples from an underlying base measure; the probability density of the transformed samples is then accessible and the normalizing flow can be trained via maximum likelihood on simulated parameter-observation pairs. A recent work [Ramesh et al., 2022] approximated instead the posterior with generative networks, which drop the invertibility requirement and are thus a more flexible class of distributions scaling to high-dimensional and structured data. However, generative networks only allow sampling from the parametrized distribution; for this reason, Ramesh et al. [2022] follows the common solution of adversarial training, where the generative network plays a min-max game against a "critic" network. This procedure is unstable and can lead to a learned distribution underestimating the uncertainty - in extreme cases collapsing to a single point. Here, we propose to approximate the posterior with generative networks trained by Scoring Rule minimization, an overlooked adversarial-free method enabling smooth training and better uncertainty quantification. In simulation studies, the Scoring Rule approach yields better performances with shorter training time with respect to the adversarial framework.

RSTGen: Imbuing Fine-Grained Interpretable Control into Long-FormText Generators

In this paper, we study the task of improving the cohesion and coherence of long-form text generated by language models. To this end, we propose RSTGen, a framework that utilises Rhetorical Structure Theory (RST), a classical language theory, to control the discourse structure, semantics and topics of generated text. Firstly, we demonstrate our model's ability to control structural discourse and semantic features of generated text in open generation evaluation. Then we experiment on the two challenging long-form text tasks of argument generation and story generation. Evaluation using automated metrics and a metric with high correlation to human evaluation, shows that our model performs competitively against existing models, while offering significantly more controls over generated text than alternative methods.

Probabilistic Forecasting with Conditional Generative Networks via Scoring Rule Minimization

Probabilistic forecasting consists of stating a probability distribution for a future outcome based on past observations. In meteorology, ensembles of physics-based numerical models are run to get such distribution. Usually, performance is evaluated with scoring rules, functions of the forecast distribution and the observed outcome. With some scoring rules, calibration and sharpness of the forecast can be assessed at the same time. In deep learning, generative neural networks parametrize distributions on high-dimensional spaces and easily allow sampling by transforming draws from a latent variable. Conditional generative networks additionally constrain the distribution on an input variable. In this manuscript, we perform probabilistic forecasting with conditional generative networks trained to minimize scoring rule values. In contrast to Generative Adversarial Networks (GANs), no discriminator is required and training is stable. We perform experiments on two chaotic models and a global dataset of weather observations; results are satisfactory and better calibrated than what achieved by GANs.

Score Matched Conditional Exponential Families for Likelihood-Free Inference

To perform Bayesian inference for stochastic simulator models for which the likelihood is not accessible, Likelihood-Free Inference (LFI) relies on simulations from the model. Standard LFI methods can be split according to how these simulations are used: to build an explicit Surrogate Likelihood, or to accept/reject parameter values according to a measure of distance from the observations (Approximate Bayesian Computation (ABC)). In both cases, simulations are adaptively tailored to the value of the observation. Here, we generate parameter-simulation pairs from the model independently on the observation, and use them to learn a conditional exponential family likelihood approximation; to parametrize it, we use Neural Networks whose weights are tuned with Score Matching. With our likelihood approximation, we can employ MCMC for doubly intractable distributions to draw samples from the posterior for any number of observations without additional model simulations, with performance competitive to comparable approaches. Further, the sufficient statistics of the exponential family can be used as summaries in ABC, outperforming the state-of-the-art method in five different models with known likelihood. Finally, we apply our method to a challenging model from meteorology.

Interpretable pathological test for Cardio-vascular disease: Approximate Bayesian computation with distance learning

Cardio/cerebrovascular diseases (CVD) have become one of the major health issue in our societies. But recent studies show that the present clinical tests to detect CVD are ineffectual as they do not consider different stages of platelet activation or the molecular dynamics involved in platelet interactions and are incapable to consider inter-individual variability. Here we propose a stochastic platelet deposition model and an inferential scheme for uncertainty quantification of these parameters using Approximate Bayesian Computation and distance learning. Finally we show that our methodology can learn biologically meaningful parameters, which are the specific dysfunctioning parameters in each type of patients, from data collected from healthy volunteers and patients. This work opens up an unprecedented opportunity of personalized pathological test for CVD detection and medical treatment. Also our proposed methodology can be used to other fields of science where we would need machine learning tools to be interpretable.

TRU-NET: A Deep Learning Approach to High Resolution Prediction of Rainfall

Climate models (CM) are used to evaluate the impact of climate change on the risk of floods and strong precipitation events. However, these numerical simulators have difficulties representing precipitation events accurately, mainly due to limited spatial resolution when simulating multi-scale dynamics in the atmosphere. To improve the prediction of high resolution precipitation we apply a Deep Learning (DL) approach using an input of CM simulations of the model fields (weather variables) that are more predictable than local precipitation. To this end, we present TRU-NET (Temporal Recurrent U-Net), an encoder-decoder model featuring a novel 2D cross attention mechanism between contiguous convolutional-recurrent layers to effectively model multi-scale spatio-temporal weather processes. We use a conditional-continuous loss function to capture the zero-skewed %extreme event patterns of rainfall. Experiments show that our model consistently attains lower RMSE and MAE scores than a DL model prevalent in short term precipitation prediction and improves upon the rainfall predictions of a state-of-the-art dynamical weather model. Moreover, by evaluating the performance of our model under various, training and testing, data formulation strategies, we show that there is enough data for our deep learning approach to output robust, high-quality results across seasons and varying regions.

Bayesian Inference of Spreading Processes on Networks

Infectious diseases are studied to understand their spreading mechanisms, to evaluate control strategies and to predict the risk and course of future outbreaks. Because people only interact with a small number of individuals, and because the structure of these interactions matters for spreading processes, the pairwise relationships between individuals in a population can be usefully represented by a network. Although the underlying processes of transmission are different, the network approach can be used to study the spread of pathogens in a contact network or the spread of rumors in an online social network. We study simulated simple and complex epidemics on synthetic networks and on two empirical networks, a social / contact network in an Indian village and an online social network in the U.S. Our goal is to learn simultaneously about the spreading process parameters and the source node (first infected node) of the epidemic, given a fixed and known network structure, and observations about state of nodes at several points in time. Our inference scheme is based on approximate Bayesian computation (ABC), an inference technique for complex models with likelihood functions that are either expensive to evaluate or analytically intractable. ABC enables us to adopt a Bayesian approach to the problem despite the posterior distribution being very complex. Our method is agnostic about the topology of the network and the nature of the spreading process. It generally performs well and, somewhat counter-intuitively, the inference problem appears to be easier on more heterogeneous network topologies, which enhances its future applicability to real-world settings where few networks have homogeneous topologies.