Measuring Data Science Automation: A Survey of Evaluation Tools for AI Assistants and Agents

Data science aims to extract insights from data to support decision-making processes. Recently, Large Language Models (LLMs) are increasingly used as assistants for data science, by suggesting ideas, techniques and small code snippets, or for the interpretation of results and reporting. Proper automation of some data-science activities is now promised by the rise of LLM agents, i.e., AI systems powered by an LLM equipped with additional affordances--such as code execution and knowledge bases--that can perform self-directed actions and interact with digital environments. In this paper, we survey the evaluation of LLM assistants and agents for data science. We find (1) a dominant focus on a small subset of goal-oriented activities, largely ignoring data management and exploratory activities; (2) a concentration on pure assistance or fully autonomous agents, without considering intermediate levels of human-AI collaboration; and (3) an emphasis on human substitution, therefore neglecting the possibility of higher levels of automation thanks to task transformation.

General Scales Unlock AI Evaluation with Explanatory and Predictive Power

Ensuring safe and effective use of AI requires understanding and anticipating its performance on novel tasks, from advanced scientific challenges to transformed workplace activities. So far, benchmarking has guided progress in AI, but it has offered limited explanatory and predictive power for general-purpose AI systems, given the low transferability across diverse tasks. In this paper, we introduce general scales for AI evaluation that can explain what common AI benchmarks really measure, extract ability profiles of AI systems, and predict their performance for new task instances, in- and out-of-distribution. Our fully-automated methodology builds on 18 newly-crafted rubrics that place instance demands on general scales that do not saturate. Illustrated for 15 large language models and 63 tasks, high explanatory power is unleashed from inspecting the demand and ability profiles, bringing insights on the sensitivity and specificity exhibited by different benchmarks, and how knowledge, metacognition and reasoning are affected by model size, chain-of-thought and distillation. Surprisingly, high predictive power at the instance level becomes possible using these demand levels, providing superior estimates over black-box baseline predictors based on embeddings or finetuning, especially in out-of-distribution settings (new tasks and new benchmarks). The scales, rubrics, battery, techniques and results presented here represent a major step for AI evaluation, underpinning the reliable deployment of AI in the years ahead.

Paradigms of AI Evaluation: Mapping Goals, Methodologies and Culture

Research in AI evaluation has grown increasingly complex and multidisciplinary, attracting researchers with diverse backgrounds and objectives. As a result, divergent evaluation paradigms have emerged, often developing in isolation, adopting conflicting terminologies, and overlooking each other's contributions. This fragmentation has led to insular research trajectories and communication barriers both among different paradigms and with the general public, contributing to unmet expectations for deployed AI systems. To help bridge this insularity, in this paper we survey recent work in the AI evaluation landscape and identify six main paradigms. We characterise major recent contributions within each paradigm across key dimensions related to their goals, methodologies and research cultures. By clarifying the unique combination of questions and approaches associated with each paradigm, we aim to increase awareness of the breadth of current evaluation approaches and foster cross-pollination between different paradigms. We also identify potential gaps in the field to inspire future research directions.

PredictaBoard: Benchmarking LLM Score Predictability

Despite possessing impressive skills, Large Language Models (LLMs) often fail unpredictably, demonstrating inconsistent success in even basic common sense reasoning tasks. This unpredictability poses a significant challenge to ensuring their safe deployment, as identifying and operating within a reliable "safe zone" is essential for mitigating risks. To address this, we present PredictaBoard, a novel collaborative benchmarking framework designed to evaluate the ability of score predictors (referred to as assessors) to anticipate LLM errors on specific task instances (i.e., prompts) from existing datasets. PredictaBoard evaluates pairs of LLMs and assessors by considering the rejection rate at different tolerance errors. As such, PredictaBoard stimulates research into developing better assessors and making LLMs more predictable, not only with a higher average performance. We conduct illustrative experiments using baseline assessors and state-of-the-art LLMs. PredictaBoard highlights the critical need to evaluate predictability alongside performance, paving the way for safer AI systems where errors are not only minimised but also anticipated and effectively mitigated. Code for our benchmark can be found at https://github.com/Kinds-of-Intelligence-CFI/PredictaBoard

Leaving the barn door open for Clever Hans: Simple features predict LLM benchmark answers

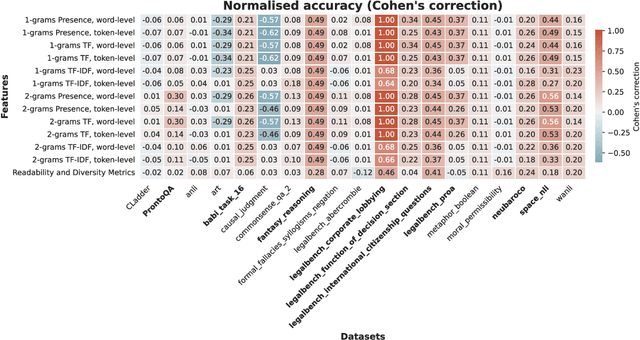
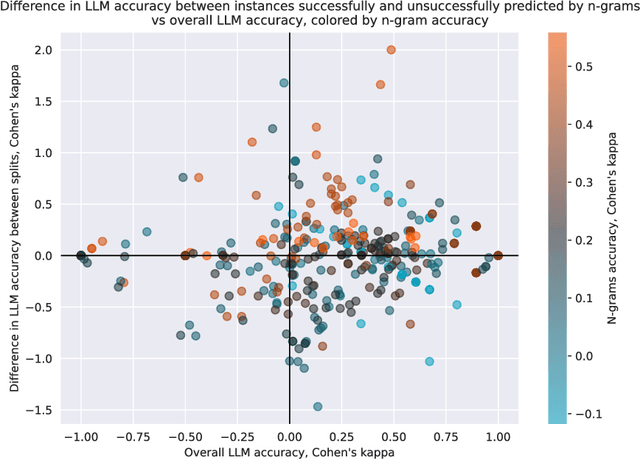
The integrity of AI benchmarks is fundamental to accurately assess the capabilities of AI systems. The internal validity of these benchmarks - i.e., making sure they are free from confounding factors - is crucial for ensuring that they are measuring what they are designed to measure. In this paper, we explore a key issue related to internal validity: the possibility that AI systems can solve benchmarks in unintended ways, bypassing the capability being tested. This phenomenon, widely known in human and animal experiments, is often referred to as the 'Clever Hans' effect, where tasks are solved using spurious cues, often involving much simpler processes than those putatively assessed. Previous research suggests that language models can exhibit this behaviour as well. In several older Natural Language Processing (NLP) benchmarks, individual $n$-grams like "not" have been found to be highly predictive of the correct labels, and supervised NLP models have been shown to exploit these patterns. In this work, we investigate the extent to which simple $n$-grams extracted from benchmark instances can be combined to predict labels in modern multiple-choice benchmarks designed for LLMs, and whether LLMs might be using such $n$-gram patterns to solve these benchmarks. We show how simple classifiers trained on these $n$-grams can achieve high scores on several benchmarks, despite lacking the capabilities being tested. Additionally, we provide evidence that modern LLMs might be using these superficial patterns to solve benchmarks. This suggests that the internal validity of these benchmarks may be compromised and caution should be exercised when interpreting LLM performance results on them.

100 instances is all you need: predicting the success of a new LLM on unseen data by testing on a few instances

Predicting the performance of LLMs on individual task instances is essential to ensure their reliability in high-stakes applications. To do so, a possibility is to evaluate the considered LLM on a set of task instances and train an assessor to predict its performance based on features of the instances. However, this approach requires evaluating each new LLM on a sufficiently large set of task instances to train an assessor specific to it. In this work, we leverage the evaluation results of previously tested LLMs to reduce the number of evaluations required to predict the performance of a new LLM. In practice, we propose to test the new LLM on a small set of reference instances and train a generic assessor which predicts the performance of the LLM on an instance based on the performance of the former on the reference set and features of the instance of interest. We conduct empirical studies on HELM-Lite and KindsOfReasoning, a collection of existing reasoning datasets that we introduce, where we evaluate all instruction-fine-tuned OpenAI models until the January 2024 version of GPT4. When predicting performance on instances with the same distribution as those used to train the generic assessor, we find this achieves performance comparable to the LLM-specific assessors trained on the full set of instances. Additionally, we find that randomly selecting the reference instances performs as well as some advanced selection methods we tested. For out of distribution, however, no clear winner emerges and the overall performance is worse, suggesting that the inherent predictability of LLMs is low.

How to Catch an AI Liar: Lie Detection in Black-Box LLMs by Asking Unrelated Questions

Large language models (LLMs) can "lie", which we define as outputting false statements despite "knowing" the truth in a demonstrable sense. LLMs might "lie", for example, when instructed to output misinformation. Here, we develop a simple lie detector that requires neither access to the LLM's activations (black-box) nor ground-truth knowledge of the fact in question. The detector works by asking a predefined set of unrelated follow-up questions after a suspected lie, and feeding the LLM's yes/no answers into a logistic regression classifier. Despite its simplicity, this lie detector is highly accurate and surprisingly general. When trained on examples from a single setting -- prompting GPT-3.5 to lie about factual questions -- the detector generalises out-of-distribution to (1) other LLM architectures, (2) LLMs fine-tuned to lie, (3) sycophantic lies, and (4) lies emerging in real-life scenarios such as sales. These results indicate that LLMs have distinctive lie-related behavioural patterns, consistent across architectures and contexts, which could enable general-purpose lie detection.

Likelihood-Free Inference with Generative Neural Networks via Scoring Rule Minimization

Bayesian Likelihood-Free Inference methods yield posterior approximations for simulator models with intractable likelihood. Recently, many works trained neural networks to approximate either the intractable likelihood or the posterior directly. Most proposals use normalizing flows, namely neural networks parametrizing invertible maps used to transform samples from an underlying base measure; the probability density of the transformed samples is then accessible and the normalizing flow can be trained via maximum likelihood on simulated parameter-observation pairs. A recent work [Ramesh et al., 2022] approximated instead the posterior with generative networks, which drop the invertibility requirement and are thus a more flexible class of distributions scaling to high-dimensional and structured data. However, generative networks only allow sampling from the parametrized distribution; for this reason, Ramesh et al. [2022] follows the common solution of adversarial training, where the generative network plays a min-max game against a "critic" network. This procedure is unstable and can lead to a learned distribution underestimating the uncertainty - in extreme cases collapsing to a single point. Here, we propose to approximate the posterior with generative networks trained by Scoring Rule minimization, an overlooked adversarial-free method enabling smooth training and better uncertainty quantification. In simulation studies, the Scoring Rule approach yields better performances with shorter training time with respect to the adversarial framework.

Probabilistic Forecasting with Conditional Generative Networks via Scoring Rule Minimization

Probabilistic forecasting consists of stating a probability distribution for a future outcome based on past observations. In meteorology, ensembles of physics-based numerical models are run to get such distribution. Usually, performance is evaluated with scoring rules, functions of the forecast distribution and the observed outcome. With some scoring rules, calibration and sharpness of the forecast can be assessed at the same time. In deep learning, generative neural networks parametrize distributions on high-dimensional spaces and easily allow sampling by transforming draws from a latent variable. Conditional generative networks additionally constrain the distribution on an input variable. In this manuscript, we perform probabilistic forecasting with conditional generative networks trained to minimize scoring rule values. In contrast to Generative Adversarial Networks (GANs), no discriminator is required and training is stable. We perform experiments on two chaotic models and a global dataset of weather observations; results are satisfactory and better calibrated than what achieved by GANs.

Score Matched Conditional Exponential Families for Likelihood-Free Inference

To perform Bayesian inference for stochastic simulator models for which the likelihood is not accessible, Likelihood-Free Inference (LFI) relies on simulations from the model. Standard LFI methods can be split according to how these simulations are used: to build an explicit Surrogate Likelihood, or to accept/reject parameter values according to a measure of distance from the observations (Approximate Bayesian Computation (ABC)). In both cases, simulations are adaptively tailored to the value of the observation. Here, we generate parameter-simulation pairs from the model independently on the observation, and use them to learn a conditional exponential family likelihood approximation; to parametrize it, we use Neural Networks whose weights are tuned with Score Matching. With our likelihood approximation, we can employ MCMC for doubly intractable distributions to draw samples from the posterior for any number of observations without additional model simulations, with performance competitive to comparable approaches. Further, the sufficient statistics of the exponential family can be used as summaries in ABC, outperforming the state-of-the-art method in five different models with known likelihood. Finally, we apply our method to a challenging model from meteorology.