Your copula is a classifier in disguise: classification-based copula density estimation
Paper and Code
Nov 05, 2024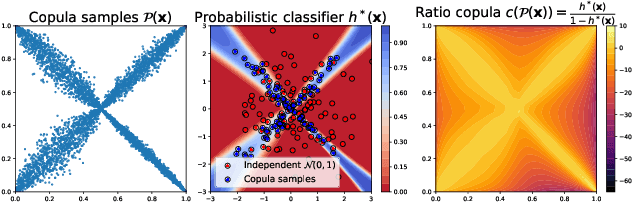

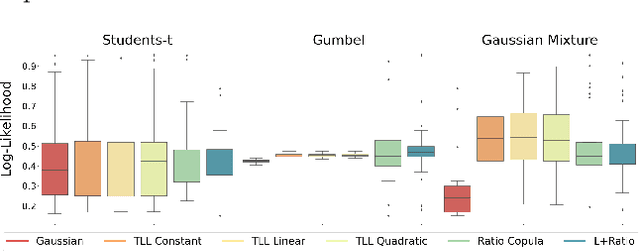

We propose reinterpreting copula density estimation as a discriminative task. Under this novel estimation scheme, we train a classifier to distinguish samples from the joint density from those of the product of independent marginals, recovering the copula density in the process. We derive equivalences between well-known copula classes and classification problems naturally arising in our interpretation. Furthermore, we show our estimator achieves theoretical guarantees akin to maximum likelihood estimation. By identifying a connection with density ratio estimation, we benefit from the rich literature and models available for such problems. Empirically, we demonstrate the applicability of our approach by estimating copulas of real and high-dimensional datasets, outperforming competing copula estimators in density evaluation as well as sampling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge