Causal Posterior Estimation

We present Causal Posterior Estimation (CPE), a novel method for Bayesian inference in simulator models, i.e., models where the evaluation of the likelihood function is intractable or too computationally expensive, but where one can simulate model outputs given parameter values. CPE utilizes a normalizing flow-based (NF) approximation to the posterior distribution which carefully incorporates the conditional dependence structure induced by the graphical representation of the model into the neural network. Thereby it is possible to improve the accuracy of the approximation. We introduce both discrete and continuous NF architectures for CPE and propose a constant-time sampling procedure for the continuous case which reduces the computational complexity of drawing samples to O(1) as for discrete NFs. We show, through an extensive experimental evaluation, that by incorporating the conditional dependencies induced by the graphical model directly into the neural network, rather than learning them from data, CPE is able to conduct highly accurate posterior inference either outperforming or matching the state of the art in the field.

Are LLMs effective psychological assessors? Leveraging adaptive RAG for interpretable mental health screening through psychometric practice

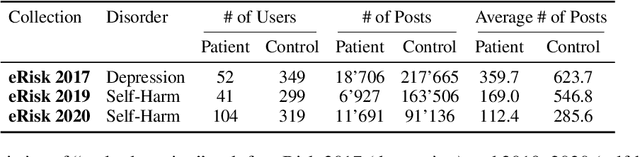
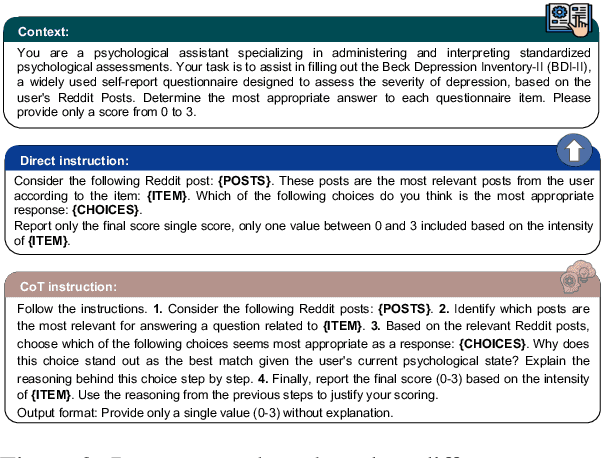
In psychological practice, standardized questionnaires serve as essential tools for assessing mental constructs (e.g., attitudes, traits, and emotions) through structured questions (aka items). With the increasing prevalence of social media platforms where users share personal experiences and emotions, researchers are exploring computational methods to leverage this data for rapid mental health screening. In this study, we propose a novel adaptive Retrieval-Augmented Generation (RAG) approach that completes psychological questionnaires by analyzing social media posts. Our method retrieves the most relevant user posts for each question in a psychological survey and uses Large Language Models (LLMs) to predict questionnaire scores in a zero-shot setting. Our findings are twofold. First we demonstrate that this approach can effectively predict users' responses to psychological questionnaires, such as the Beck Depression Inventory II (BDI-II), achieving performance comparable to or surpassing state-of-the-art models on Reddit-based benchmark datasets without relying on training data. Second, we show how this methodology can be generalized as a scalable screening tool, as the final assessment is systematically derived by completing standardized questionnaires and tracking how individual item responses contribute to the diagnosis, aligning with established psychometric practices.

Simulation-based inference with the Python Package sbijax

Neural simulation-based inference (SBI) describes an emerging family of methods for Bayesian inference with intractable likelihood functions that use neural networks as surrogate models. Here we introduce sbijax, a Python package that implements a wide variety of state-of-the-art methods in neural simulation-based inference using a user-friendly programming interface. sbijax offers high-level functionality to quickly construct SBI estimators, and compute and visualize posterior distributions with only a few lines of code. In addition, the package provides functionality for conventional approximate Bayesian computation, to compute model diagnostics, and to automatically estimate summary statistics. By virtue of being entirely written in JAX, sbijax is extremely computationally efficient, allowing rapid training of neural networks and executing code automatically in parallel on both CPU and GPU.

Federated Learning for Non-factorizable Models using Deep Generative Prior Approximations

Federated learning (FL) allows for collaborative model training across decentralized clients while preserving privacy by avoiding data sharing. However, current FL methods assume conditional independence between client models, limiting the use of priors that capture dependence, such as Gaussian processes (GPs). We introduce the Structured Independence via deep Generative Model Approximation (SIGMA) prior which enables FL for non-factorizable models across clients, expanding the applicability of FL to fields such as spatial statistics, epidemiology, environmental science, and other domains where modeling dependencies is crucial. The SIGMA prior is a pre-trained deep generative model that approximates the desired prior and induces a specified conditional independence structure in the latent variables, creating an approximate model suitable for FL settings. We demonstrate the SIGMA prior's effectiveness on synthetic data and showcase its utility in a real-world example of FL for spatial data, using a conditional autoregressive prior to model spatial dependence across Australia. Our work enables new FL applications in domains where modeling dependent data is essential for accurate predictions and decision-making.

Beyond the noise: intrinsic dimension estimation with optimal neighbourhood identification

The Intrinsic Dimension (ID) is a key concept in unsupervised learning and feature selection, as it is a lower bound to the number of variables which are necessary to describe a system. However, in almost any real-world dataset the ID depends on the scale at which the data are analysed. Quite typically at a small scale, the ID is very large, as the data are affected by measurement errors. At large scale, the ID can also be erroneously large, due to the curvature and the topology of the manifold containing the data. In this work, we introduce an automatic protocol to select the sweet spot, namely the correct range of scales in which the ID is meaningful and useful. This protocol is based on imposing that for distances smaller than the correct scale the density of the data is constant. Since to estimate the density it is necessary to know the ID, this condition is imposed self-consistently. We illustrate the usefulness and robustness of this procedure by benchmarks on artificial and real-world datasets.

Scalable Vertical Federated Learning via Data Augmentation and Amortized Inference

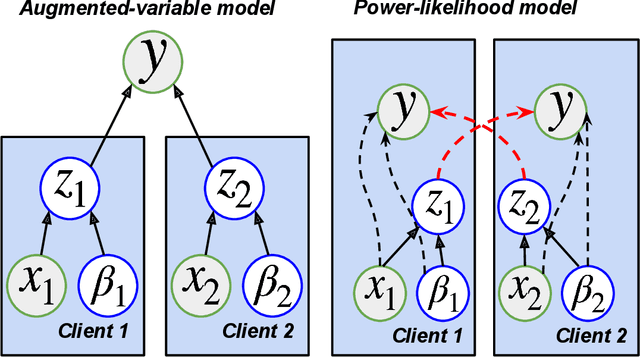
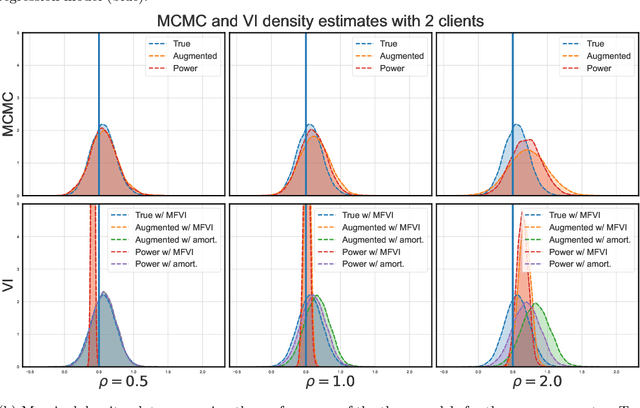
Vertical federated learning (VFL) has emerged as a paradigm for collaborative model estimation across multiple clients, each holding a distinct set of covariates. This paper introduces the first comprehensive framework for fitting Bayesian models in the VFL setting. We propose a novel approach that leverages data augmentation techniques to transform VFL problems into a form compatible with existing Bayesian federated learning algorithms. We present an innovative model formulation for specific VFL scenarios where the joint likelihood factorizes into a product of client-specific likelihoods. To mitigate the dimensionality challenge posed by data augmentation, which scales with the number of observations and clients, we develop a factorized amortized variational approximation that achieves scalability independent of the number of observations. We showcase the efficacy of our framework through extensive numerical experiments on logistic regression, multilevel regression, and a novel hierarchical Bayesian split neural net model. Our work paves the way for privacy-preserving, decentralized Bayesian inference in vertically partitioned data scenarios, opening up new avenues for research and applications in various domains.

On the intrinsic dimensionality of Covid-19 data: a global perspective

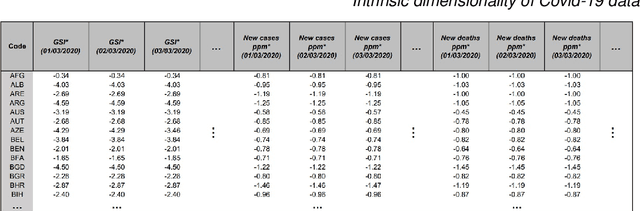
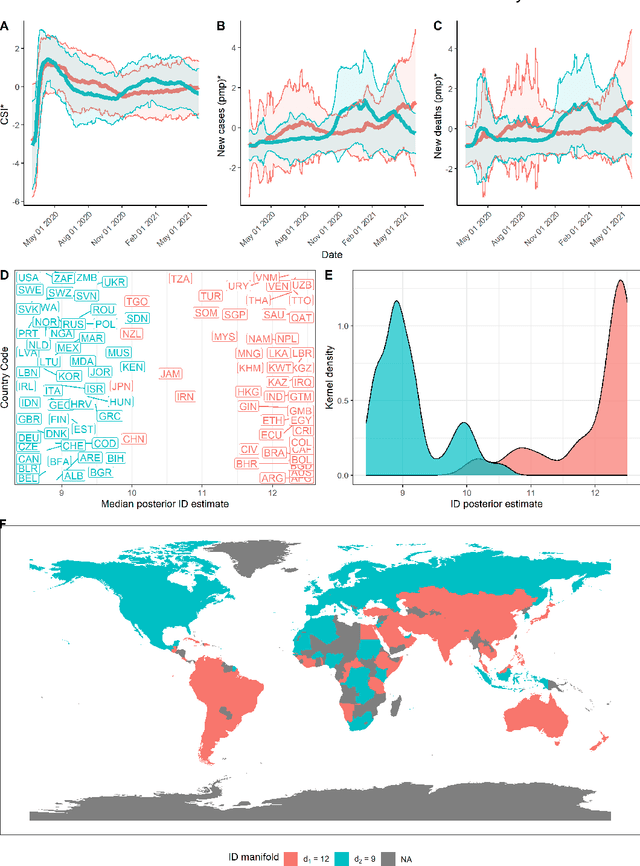
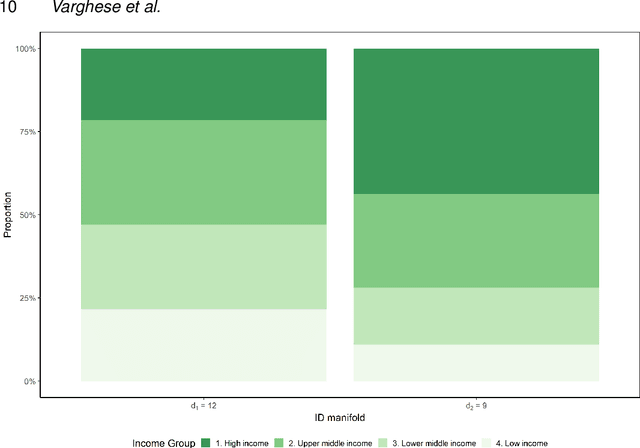
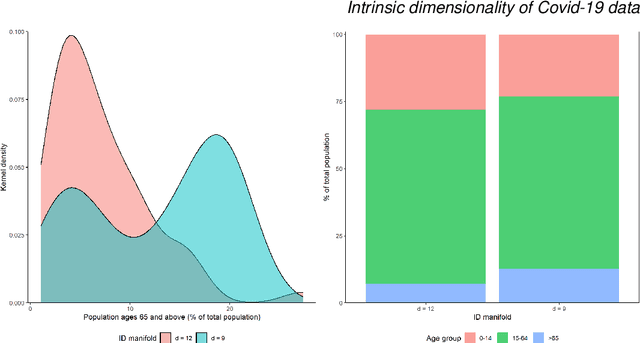
This paper aims to develop a global perspective of the complexity of the relationship between the standardised per-capita growth rate of Covid-19 cases, deaths, and the OxCGRT Covid-19 Stringency Index, a measure describing a country's stringency of lockdown policies. To achieve our goal, we use a heterogeneous intrinsic dimension estimator implemented as a Bayesian mixture model, called Hidalgo. We identify that the Covid-19 dataset may project onto two low-dimensional manifolds without significant information loss. The low dimensionality suggests strong dependency among the standardised growth rates of cases and deaths per capita and the OxCGRT Covid-19 Stringency Index for a country over 2020-2021. Given the low dimensional structure, it may be feasible to model observable Covid-19 dynamics with few parameters. Importantly, we identify spatial autocorrelation in the intrinsic dimension distribution worldwide. Moreover, we highlight that high-income countries are more likely to lie on low-dimensional manifolds, likely arising from aging populations, comorbidities, and increased per capita mortality burden from Covid-19. Finally, we temporally stratify the dataset to examine the intrinsic dimension at a more granular level throughout the Covid-19 pandemic.

Learning Summary Statistics for Bayesian Inference with Autoencoders

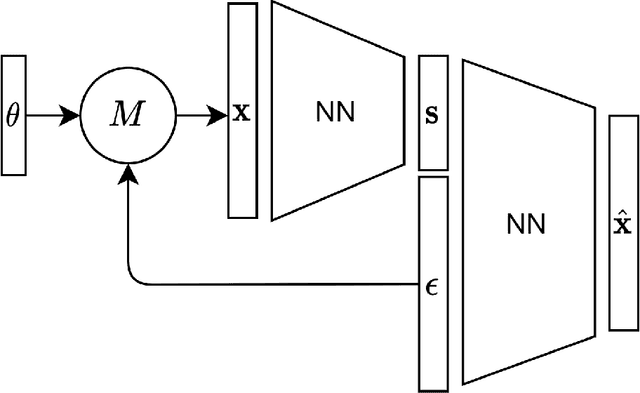
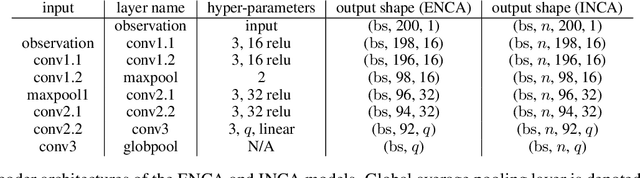
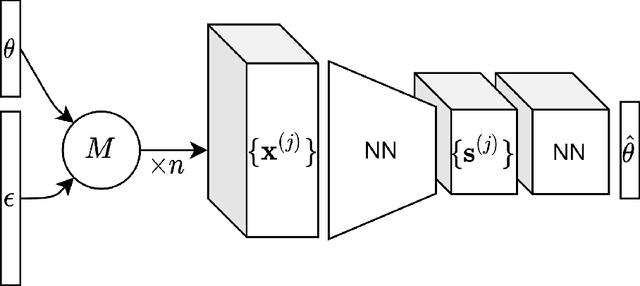
For stochastic models with intractable likelihood functions, approximate Bayesian computation offers a way of approximating the true posterior through repeated comparisons of observations with simulated model outputs in terms of a small set of summary statistics. These statistics need to retain the information that is relevant for constraining the parameters but cancel out the noise. They can thus be seen as thermodynamic state variables, for general stochastic models. For many scientific applications, we need strictly more summary statistics than model parameters to reach a satisfactory approximation of the posterior. Therefore, we propose to use the inner dimension of deep neural network based Autoencoders as summary statistics. To create an incentive for the encoder to encode all the parameter-related information but not the noise, we give the decoder access to explicit or implicit information on the noise that has been used to generate the training data. We validate the approach empirically on two types of stochastic models.

Interpretable pathological test for Cardio-vascular disease: Approximate Bayesian computation with distance learning

Cardio/cerebrovascular diseases (CVD) have become one of the major health issue in our societies. But recent studies show that the present clinical tests to detect CVD are ineffectual as they do not consider different stages of platelet activation or the molecular dynamics involved in platelet interactions and are incapable to consider inter-individual variability. Here we propose a stochastic platelet deposition model and an inferential scheme for uncertainty quantification of these parameters using Approximate Bayesian Computation and distance learning. Finally we show that our methodology can learn biologically meaningful parameters, which are the specific dysfunctioning parameters in each type of patients, from data collected from healthy volunteers and patients. This work opens up an unprecedented opportunity of personalized pathological test for CVD detection and medical treatment. Also our proposed methodology can be used to other fields of science where we would need machine learning tools to be interpretable.

Clustering by the local intrinsic dimension: the hidden structure of real-world data

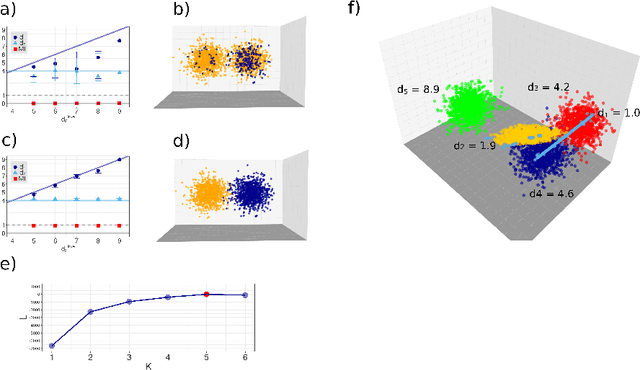
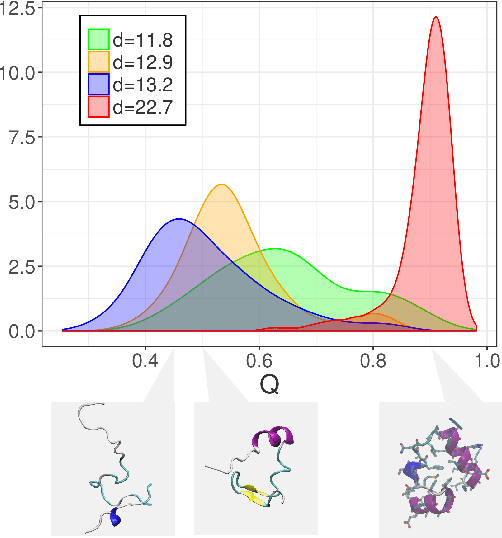
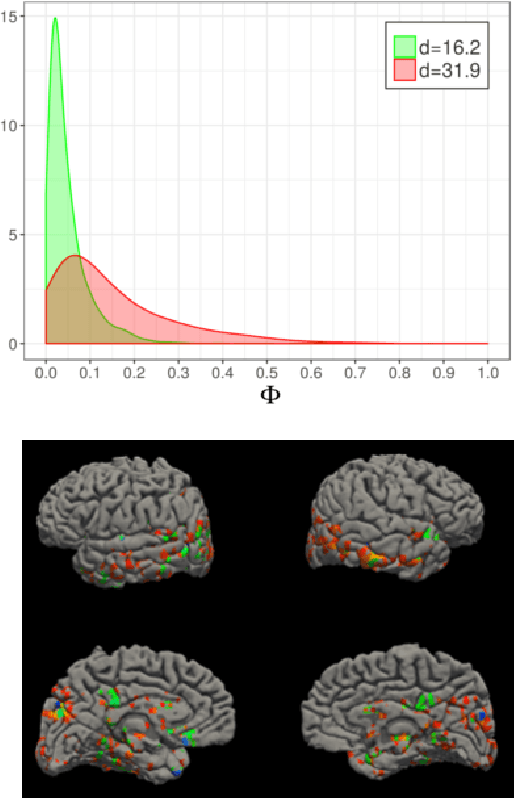
It is well known that a small number of variables is often sufficient to effectively describe high-dimensional data. This number is called the intrinsic dimension (ID) of the data. What is not so commonly known is that the ID can vary within the same dataset. This fact has been highlighted in technical discussions, but seldom exploited to gain practical insight in the data structure. Here we develop a simple and robust approach to cluster regions with the same local ID in a given data landscape. Surprisingly, we find that many real-world data sets contain regions with widely heterogeneous dimensions. These regions host points differing in core properties: folded vs unfolded configurations in a protein molecular dynamics trajectory, active vs non-active regions in brain imaging data, and firms with different financial risk in company balance sheets. Our results show that a simple topological feature, the local ID, is sufficient to uncover a rich structure in high-dimensional data landscapes.