Simulation-based inference with the Python Package sbijax

Neural simulation-based inference (SBI) describes an emerging family of methods for Bayesian inference with intractable likelihood functions that use neural networks as surrogate models. Here we introduce sbijax, a Python package that implements a wide variety of state-of-the-art methods in neural simulation-based inference using a user-friendly programming interface. sbijax offers high-level functionality to quickly construct SBI estimators, and compute and visualize posterior distributions with only a few lines of code. In addition, the package provides functionality for conventional approximate Bayesian computation, to compute model diagnostics, and to automatically estimate summary statistics. By virtue of being entirely written in JAX, sbijax is extremely computationally efficient, allowing rapid training of neural networks and executing code automatically in parallel on both CPU and GPU.

Simulation-based inference using surjective sequential neural likelihood estimation

We present Surjective Sequential Neural Likelihood (SSNL) estimation, a novel method for simulation-based inference in models where the evaluation of the likelihood function is not tractable and only a simulator that can generate synthetic data is available. SSNL fits a dimensionality-reducing surjective normalizing flow model and uses it as a surrogate likelihood function which allows for conventional Bayesian inference using either Markov chain Monte Carlo methods or variational inference. By embedding the data in a low-dimensional space, SSNL solves several issues previous likelihood-based methods had when applied to high-dimensional data sets that, for instance, contain non-informative data dimensions or lie along a lower-dimensional manifold. We evaluate SSNL on a wide variety of experiments and show that it generally outperforms contemporary methods used in simulation-based inference, for instance, on a challenging real-world example from astrophysics which models the magnetic field strength of the sun using a solar dynamo model.

Learning Summary Statistics for Bayesian Inference with Autoencoders

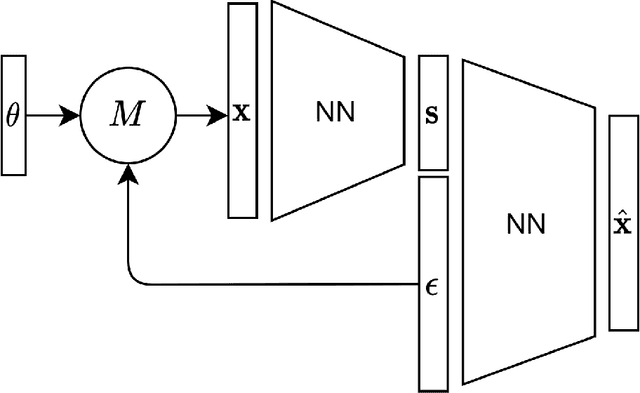
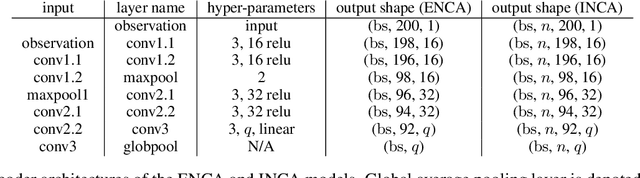
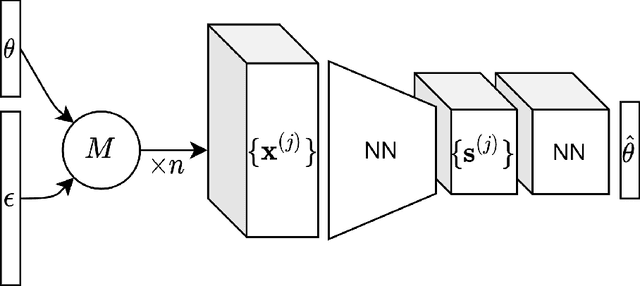
For stochastic models with intractable likelihood functions, approximate Bayesian computation offers a way of approximating the true posterior through repeated comparisons of observations with simulated model outputs in terms of a small set of summary statistics. These statistics need to retain the information that is relevant for constraining the parameters but cancel out the noise. They can thus be seen as thermodynamic state variables, for general stochastic models. For many scientific applications, we need strictly more summary statistics than model parameters to reach a satisfactory approximation of the posterior. Therefore, we propose to use the inner dimension of deep neural network based Autoencoders as summary statistics. To create an incentive for the encoder to encode all the parameter-related information but not the noise, we give the decoder access to explicit or implicit information on the noise that has been used to generate the training data. We validate the approach empirically on two types of stochastic models.

Appraisal of data-driven and mechanistic emulators of nonlinear hydrodynamic urban drainage simulators

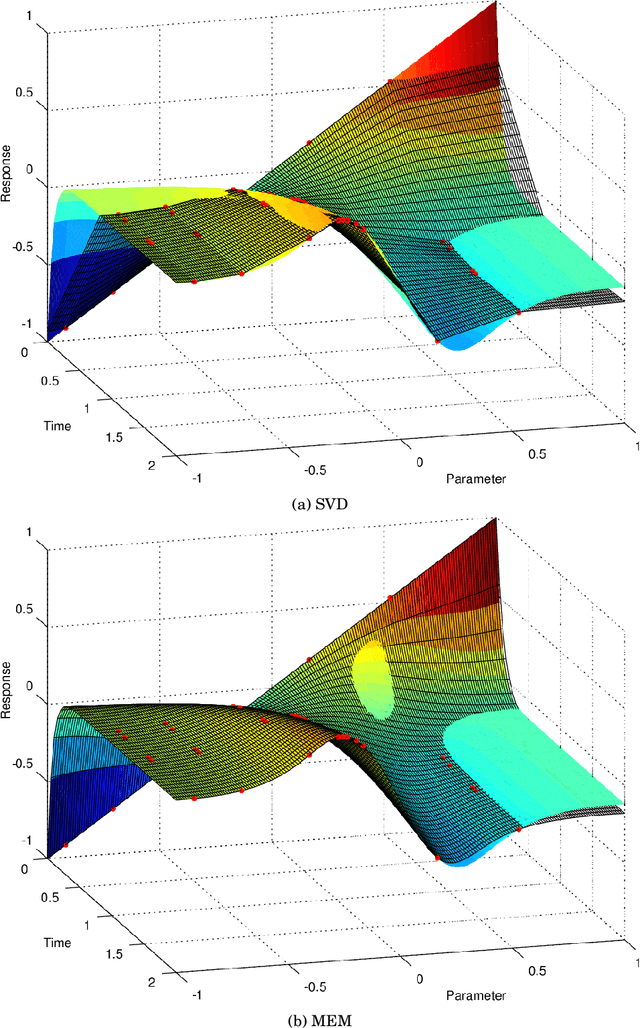
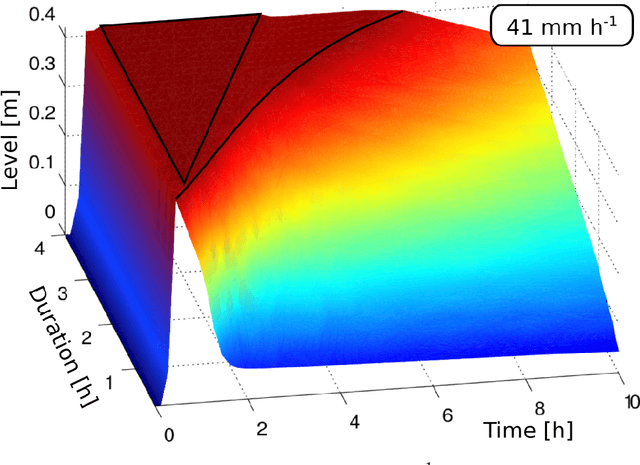
Many model based scientific and engineering methodologies, such as system identification, sensitivity analysis, optimization and control, require a large number of model evaluations. In particular, model based real-time control of urban water infrastructures and online flood alarm systems require fast prediction of the network response at different actuation and/or parameter values. General purpose urban drainage simulators are too slow for this application. Fast surrogate models, so-called emulators, provide a solution to this efficiency demand. Emulators are attractive, because they sacrifice unneeded accuracy in favor of speed. However, they have to be fine-tuned to predict the system behavior satisfactorily. Also, some emulators fail to extrapolate the system behavior beyond the training set. Although, there are many strategies for developing emulators, up until now the selection of the emulation strategy remains subjective. In this paper, we therefore compare the performance of two families of emulators for open channel flows in the context of urban drainage simulators. We compare emulators that explicitly use knowledge of the simulator's equations, i.e. mechanistic emulators based on Gaussian Processes, with purely data-driven emulators using matrix factorization. Our results suggest that in many urban applications, naive data-driven emulation outperforms mechanistic emulation. Nevertheless, we discuss scenarios in which we think that mechanistic emulation might be favorable for i) extrapolation in time and ii) dealing with sparse and unevenly sampled data. We also provide many references to advances in the field of Machine Learning that have not yet permeated into the Bayesian environmental science community.

A Simulated Annealing Approach to Bayesian Inference

A generic algorithm for the extraction of probabilistic (Bayesian) information about model parameters from data is presented. The algorithm propagates an ensemble of particles in the product space of model parameters and outputs. Each particle update consists of a random jump in parameter space followed by a simulation of a model output and a Metropolis acceptance/rejection step based on a comparison of the simulated output to the data. The distance of a particle to the data is interpreted as an energy and the algorithm is reducing the associated temperature of the ensemble such that entropy production is minimized. If this simulated annealing is not too fast compared to the mixing speed in parameter space, the parameter marginal of the ensemble approaches the Bayesian posterior distribution. Annealing is adaptive and depends on certain extensive thermodynamic quantities that can easily be measured throughout run-time. In the general case, we propose annealing with a constant entropy production rate, which is optimal as long as annealing is not too fast. For the practically relevant special case of no prior knowledge, we derive an optimal fast annealing schedule with a non-constant entropy production rate. The algorithm does not require the calculation of the density of the model likelihood, which makes it interesting for Bayesian parameter inference with stochastic models, whose likelihood functions are typically very high dimensional integrals.