From Mice to Trains: Amortized Bayesian Inference on Graph Data

Graphs arise across diverse domains, from biology and chemistry to social and information networks, as well as in transportation and logistics. Inference on graph-structured data requires methods that are permutation-invariant, scalable across varying sizes and sparsities, and capable of capturing complex long-range dependencies, making posterior estimation on graph parameters particularly challenging. Amortized Bayesian Inference (ABI) is a simulation-based framework that employs generative neural networks to enable fast, likelihood-free posterior inference. We adapt ABI to graph data to address these challenges to perform inference on node-, edge-, and graph-level parameters. Our approach couples permutation-invariant graph encoders with flexible neural posterior estimators in a two-module pipeline: a summary network maps attributed graphs to fixed-length representations, and an inference network approximates the posterior over parameters. In this setting, several neural architectures can serve as the summary network. In this work we evaluate multiple architectures and assess their performance on controlled synthetic settings and two real-world domains - biology and logistics - in terms of recovery and calibration.

Scalable Spatiotemporal Inference with Biased Scan Attention Transformer Neural Processes

Neural Processes (NPs) are a rapidly evolving class of models designed to directly model the posterior predictive distribution of stochastic processes. While early architectures were developed primarily as a scalable alternative to Gaussian Processes (GPs), modern NPs tackle far more complex and data hungry applications spanning geology, epidemiology, climate, and robotics. These applications have placed increasing pressure on the scalability of these models, with many architectures compromising accuracy for scalability. In this paper, we demonstrate that this tradeoff is often unnecessary, particularly when modeling fully or partially translation invariant processes. We propose a versatile new architecture, the Biased Scan Attention Transformer Neural Process (BSA-TNP), which introduces Kernel Regression Blocks (KRBlocks), group-invariant attention biases, and memory-efficient Biased Scan Attention (BSA). BSA-TNP is able to: (1) match or exceed the accuracy of the best models while often training in a fraction of the time, (2) exhibit translation invariance, enabling learning at multiple resolutions simultaneously, (3) transparently model processes that evolve in both space and time, (4) support high dimensional fixed effects, and (5) scale gracefully -- running inference with over 1M test points with 100K context points in under a minute on a single 24GB GPU.

DeepRV: pre-trained spatial priors for accelerated disease mapping

Recently introduced prior-encoding deep generative models (e.g., PriorVAE, $\pi$VAE, and PriorCVAE) have emerged as powerful tools for scalable Bayesian inference by emulating complex stochastic processes like Gaussian processes (GPs). However, these methods remain largely a proof-of-concept and inaccessible to practitioners. We propose DeepRV, a lightweight, decoder-only approach that accelerates training, and enhances real-world applicability in comparison to current VAE-based prior encoding approaches. Leveraging probabilistic programming frameworks (e.g., NumPyro) for inference, DeepRV achieves significant speedups while also improving the quality of parameter inference, closely matching full MCMC sampling. We showcase its effectiveness in process emulation and spatial analysis of the UK using simulated data, gender-wise cancer mortality rates for individuals under 50, and HIV prevalence in Zimbabwe. To bridge the gap between theory and practice, we provide a user-friendly API, enabling scalable and efficient Bayesian inference.

Case for a unified surrogate modelling framework in the age of AI

Surrogate models are widely used in natural sciences, engineering, and machine learning to approximate complex systems and reduce computational costs. However, the current landscape lacks standardisation across key stages of the pipeline, including data collection, sampling design, model class selection, evaluation metrics, and downstream task performance analysis. This fragmentation limits reproducibility, reliability, and cross-domain applicability. The issue has only been exacerbated by the AI revolution and a new suite of surrogate model classes that it offers. In this position paper, we argue for the urgent need for a unified framework to guide the development and evaluation of surrogate models. We outline essential steps for constructing a comprehensive pipeline and discuss alternative perspectives, such as the benefits of domain-specific frameworks. By advocating for a standardised approach, this paper seeks to improve the reliability of surrogate modelling, foster cross-disciplinary knowledge transfer, and, as a result, accelerate scientific progress.

Transformer Neural Processes -- Kernel Regression

Stochastic processes model various natural phenomena from disease transmission to stock prices, but simulating and quantifying their uncertainty can be computationally challenging. For example, modeling a Gaussian Process with standard statistical methods incurs an $\mathcal{O}(n^3)$ penalty, and even using state-of-the-art Neural Processes (NPs) incurs an $\mathcal{O}(n^2)$ penalty due to the attention mechanism. We introduce the Transformer Neural Process - Kernel Regression (TNP-KR), a new architecture that incorporates a novel transformer block we call a Kernel Regression Block (KRBlock), which reduces the computational complexity of attention in transformer-based Neural Processes (TNPs) from $\mathcal{O}((n_C+n_T)^2)$ to $O(n_C^2+n_Cn_T)$ by eliminating masked computations, where $n_C$ is the number of context, and $n_T$ is the number of test points, respectively, and a fast attention variant that further reduces all attention calculations to $\mathcal{O}(n_C)$ in space and time complexity. In benchmarks spanning such tasks as meta-regression, Bayesian optimization, and image completion, we demonstrate that the full variant matches the performance of state-of-the-art methods while training faster and scaling two orders of magnitude higher in number of test points, and the fast variant nearly matches that performance while scaling to millions of both test and context points on consumer hardware.

You are what you eat? Feeding foundation models a regionally diverse food dataset of World Wide Dishes

Foundation models are increasingly ubiquitous in our daily lives, used in everyday tasks such as text-image searches, interactions with chatbots, and content generation. As use increases, so does concern over the disparities in performance and fairness of these models for different people in different parts of the world. To assess these growing regional disparities, we present World Wide Dishes, a mixed text and image dataset consisting of 765 dishes, with dish names collected in 131 local languages. World Wide Dishes has been collected purely through human contribution and decentralised means, by creating a website widely distributed through social networks. Using the dataset, we demonstrate a novel means of operationalising capability and representational biases in foundation models such as language models and text-to-image generative models. We enrich these studies with a pilot community review to understand, from a first-person perspective, how these models generate images for people in five African countries and the United States. We find that these models generally do not produce quality text and image outputs of dishes specific to different regions. This is true even for the US, which is typically considered to be more well-resourced in training data - though the generation of US dishes does outperform that of the investigated African countries. The models demonstrate a propensity to produce outputs that are inaccurate as well as culturally misrepresentative, flattening, and insensitive. These failures in capability and representational bias have the potential to further reinforce stereotypes and disproportionately contribute to erasure based on region. The dataset and code are available at https://github.com/oxai/world-wide-dishes/.

Federated Learning for Non-factorizable Models using Deep Generative Prior Approximations

Federated learning (FL) allows for collaborative model training across decentralized clients while preserving privacy by avoiding data sharing. However, current FL methods assume conditional independence between client models, limiting the use of priors that capture dependence, such as Gaussian processes (GPs). We introduce the Structured Independence via deep Generative Model Approximation (SIGMA) prior which enables FL for non-factorizable models across clients, expanding the applicability of FL to fields such as spatial statistics, epidemiology, environmental science, and other domains where modeling dependencies is crucial. The SIGMA prior is a pre-trained deep generative model that approximates the desired prior and induces a specified conditional independence structure in the latent variables, creating an approximate model suitable for FL settings. We demonstrate the SIGMA prior's effectiveness on synthetic data and showcase its utility in a real-world example of FL for spatial data, using a conditional autoregressive prior to model spatial dependence across Australia. Our work enables new FL applications in domains where modeling dependent data is essential for accurate predictions and decision-making.

Deep learning and MCMC with aggVAE for shifting administrative boundaries: mapping malaria prevalence in Kenya

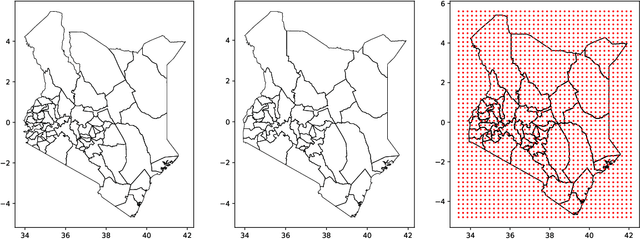
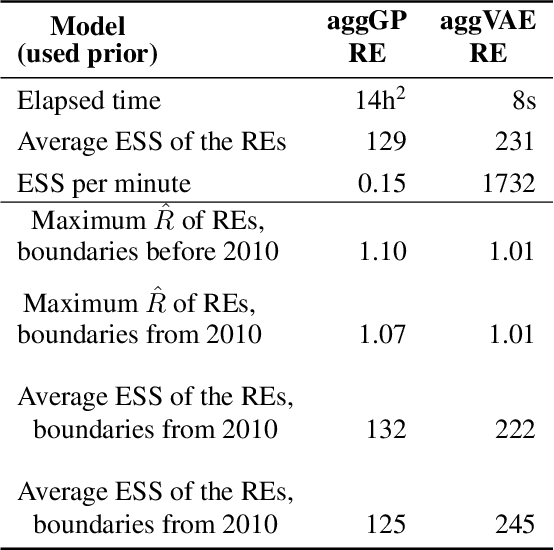
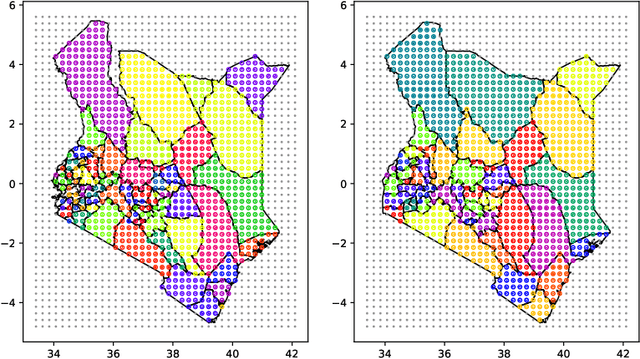
Model-based disease mapping remains a fundamental policy-informing tool in public health and disease surveillance with hierarchical Bayesian models being the current state-of-the-art approach. When working with areal data, e.g. aggregates at the administrative unit level such as district or province, routinely used models rely on the adjacency structure of areal units to account for spatial correlations. The goal of disease surveillance systems is to track disease outcomes over time, but this provides challenging in situations of crises, such as political changes, leading to changes of administrative boundaries. Kenya is an example of such country. Moreover, adjacency-based approach ignores the continuous nature of spatial processes and cannot solve the change-of-support problem, i.e. when administrative boundaries change. We present a novel, practical, and easy to implement solution relying on a methodology combining deep generative modelling and fully Bayesian inference. We build on the recent work of PriorVAE able to encode spatial priors over small areas with variational autoencoders, to map malaria prevalence in Kenya. We solve the change-of-support problem arising from Kenya changing its district boundaries in 2010. We draw realisations of the Gaussian Process (GP) prior over a fine artificial spatial grid representing continuous space and then aggregate these realisations to the level of administrative boundaries. The aggregated values are then encoded using the PriorVAE technique. The trained priors (aggVAE) are then used at the inference stage instead of the GP priors within a Markov chain Monte Carlo (MCMC) scheme. We demonstrate that it is possible to use the flexible and appropriate model for areal data based on aggregation of continuous priors, and that inference is orders of magnitude faster when using aggVAE than combining the original GP priors and the aggregation step.

PriorCVAE: scalable MCMC parameter inference with Bayesian deep generative modelling

In applied fields where the speed of inference and model flexibility are crucial, the use of Bayesian inference for models with a stochastic process as their prior, e.g. Gaussian processes (GPs) is ubiquitous. Recent literature has demonstrated that the computational bottleneck caused by GP priors or their finite realizations can be encoded using deep generative models such as variational autoencoders (VAEs), and the learned generators can then be used instead of the original priors during Markov chain Monte Carlo (MCMC) inference in a drop-in manner. While this approach enables fast and highly efficient inference, it loses information about the stochastic process hyperparameters, and, as a consequence, makes inference over hyperparameters impossible and the learned priors indistinct. We propose to resolve this issue and disentangle the learned priors by conditioning the VAE on stochastic process hyperparameters. This way, the hyperparameters are encoded alongside GP realisations and can be explicitly estimated at the inference stage. We believe that the new method, termed PriorCVAE, will be a useful tool among approximate inference approaches and has the potential to have a large impact on spatial and spatiotemporal inference in crucial real-life applications. Code showcasing PriorCVAE can be found on GitHub: https://github.com/elizavetasemenova/PriorCVAE

Encoding spatiotemporal priors with VAEs for small-area estimation

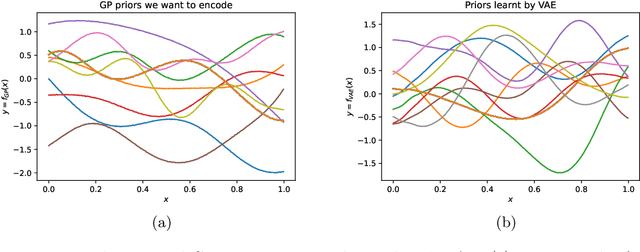
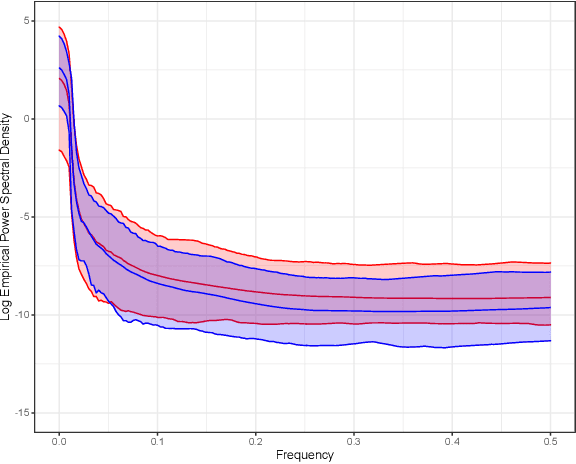
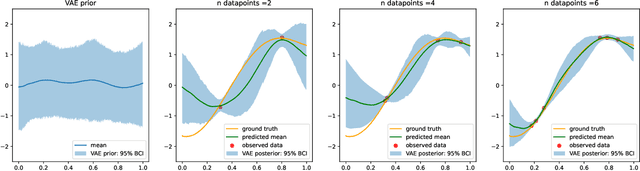
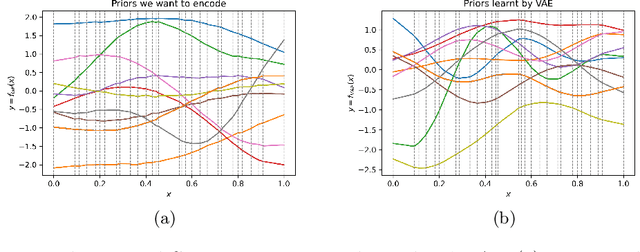
Gaussian processes (GPs), implemented through multivariate Gaussian distributions for a finite collection of data, are the most popular approach in small-area spatiotemporal statistical modelling. In this context they are used to encode correlation structures over space and time and can generalise well in interpolation tasks. Despite their flexibility, off-the-shelf GPs present serious computational challenges which limit their scalability and practical usefulness in applied settings. Here, we propose a novel, deep generative modelling approach to tackle this challenge: for a particular spatiotemporal setting, we approximate a class of GP priors through prior sampling and subsequent fitting of a variational autoencoder (VAE). Given a trained VAE, the resultant decoder allows spatiotemporal inference to become incredibly efficient due to the low dimensional, independently distributed latent Gaussian space representation of the VAE. Once trained, inference using the VAE decoder replaces the GP within a Bayesian sampling framework. This approach provides tractable and easy-to-implement means of approximately encoding spatiotemporal priors and facilitates efficient statistical inference. We demonstrate the utility of our VAE two stage approach on Bayesian, small-area estimation tasks.