Scalable Spatiotemporal Inference with Biased Scan Attention Transformer Neural Processes

Neural Processes (NPs) are a rapidly evolving class of models designed to directly model the posterior predictive distribution of stochastic processes. While early architectures were developed primarily as a scalable alternative to Gaussian Processes (GPs), modern NPs tackle far more complex and data hungry applications spanning geology, epidemiology, climate, and robotics. These applications have placed increasing pressure on the scalability of these models, with many architectures compromising accuracy for scalability. In this paper, we demonstrate that this tradeoff is often unnecessary, particularly when modeling fully or partially translation invariant processes. We propose a versatile new architecture, the Biased Scan Attention Transformer Neural Process (BSA-TNP), which introduces Kernel Regression Blocks (KRBlocks), group-invariant attention biases, and memory-efficient Biased Scan Attention (BSA). BSA-TNP is able to: (1) match or exceed the accuracy of the best models while often training in a fraction of the time, (2) exhibit translation invariance, enabling learning at multiple resolutions simultaneously, (3) transparently model processes that evolve in both space and time, (4) support high dimensional fixed effects, and (5) scale gracefully -- running inference with over 1M test points with 100K context points in under a minute on a single 24GB GPU.

Indirect Query Bayesian Optimization with Integrated Feedback

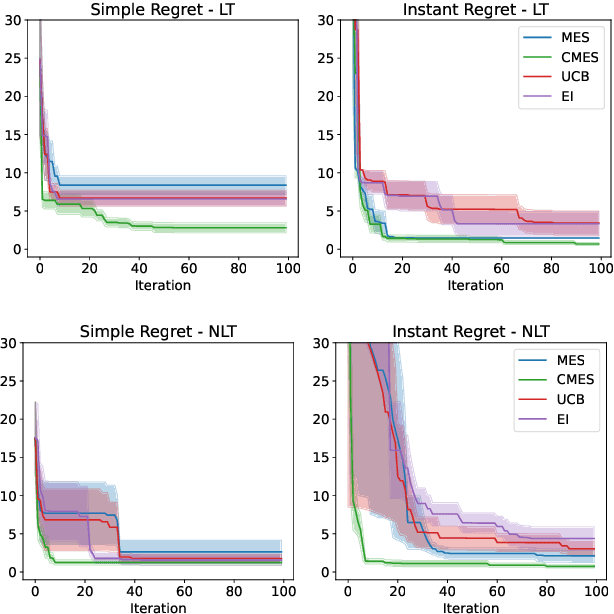
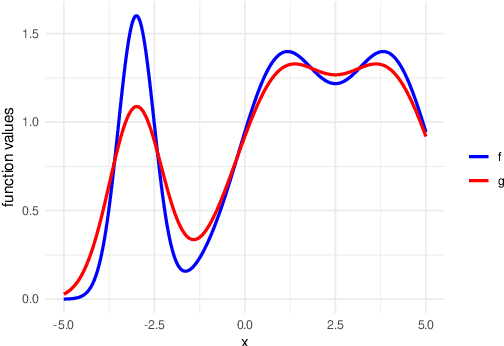
We develop the framework of Indirect Query Bayesian Optimization (IQBO), a new class of Bayesian optimization problems where the integrated feedback is given via a conditional expectation of the unknown function $f$ to be optimized. The underlying conditional distribution can be unknown and learned from data. The goal is to find the global optimum of $f$ by adaptively querying and observing in the space transformed by the conditional distribution. This is motivated by real-world applications where one cannot access direct feedback due to privacy, hardware or computational constraints. We propose the Conditional Max-Value Entropy Search (CMES) acquisition function to address this novel setting, and propose a hierarchical search algorithm to address the multi-resolution setting and improve the computational efficiency. We show regret bounds for our proposed methods and demonstrate the effectiveness of our approaches on simulated optimization tasks.

Uncertainty-Aware Regression for Socio-Economic Estimation via Multi-View Remote Sensing

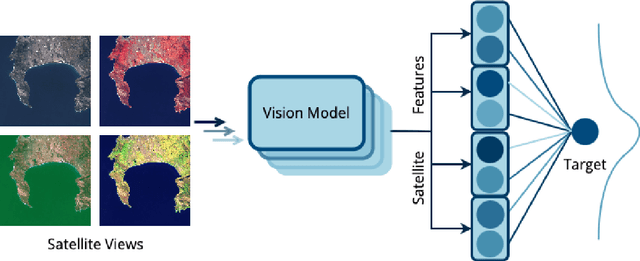
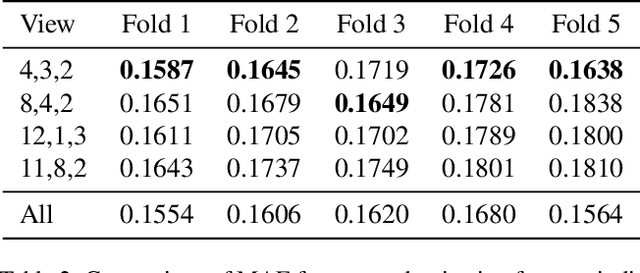
Remote sensing imagery offers rich spectral data across extensive areas for Earth observation. Many attempts have been made to leverage these data with transfer learning to develop scalable alternatives for estimating socio-economic conditions, reducing reliance on expensive survey-collected data. However, much of this research has primarily focused on daytime satellite imagery due to the limitation that most pre-trained models are trained on 3-band RGB images. Consequently, modeling techniques for spectral bands beyond the visible spectrum have not been thoroughly investigated. Additionally, quantifying uncertainty in remote sensing regression has been less explored, yet it is essential for more informed targeting and iterative collection of ground truth survey data. In this paper, we introduce a novel framework that leverages generic foundational vision models to process remote sensing imagery using combinations of three spectral bands to exploit multi-spectral data. We also employ methods such as heteroscedastic regression and Bayesian modeling to generate uncertainty estimates for the predictions. Experimental results demonstrate that our method outperforms existing models that use RGB or multi-spectral models with unstructured band usage. Moreover, our framework helps identify uncertain predictions, guiding future ground truth data acquisition.

Transformer Neural Processes -- Kernel Regression

Stochastic processes model various natural phenomena from disease transmission to stock prices, but simulating and quantifying their uncertainty can be computationally challenging. For example, modeling a Gaussian Process with standard statistical methods incurs an $\mathcal{O}(n^3)$ penalty, and even using state-of-the-art Neural Processes (NPs) incurs an $\mathcal{O}(n^2)$ penalty due to the attention mechanism. We introduce the Transformer Neural Process - Kernel Regression (TNP-KR), a new architecture that incorporates a novel transformer block we call a Kernel Regression Block (KRBlock), which reduces the computational complexity of attention in transformer-based Neural Processes (TNPs) from $\mathcal{O}((n_C+n_T)^2)$ to $O(n_C^2+n_Cn_T)$ by eliminating masked computations, where $n_C$ is the number of context, and $n_T$ is the number of test points, respectively, and a fast attention variant that further reduces all attention calculations to $\mathcal{O}(n_C)$ in space and time complexity. In benchmarks spanning such tasks as meta-regression, Bayesian optimization, and image completion, we demonstrate that the full variant matches the performance of state-of-the-art methods while training faster and scaling two orders of magnitude higher in number of test points, and the fast variant nearly matches that performance while scaling to millions of both test and context points on consumer hardware.

Graph Agnostic Causal Bayesian Optimisation

We study the problem of globally optimising a target variable of an unknown causal graph on which a sequence of soft or hard interventions can be performed. The problem of optimising the target variable associated with a causal graph is formalised as Causal Bayesian Optimisation (CBO). We study the CBO problem under the cumulative regret objective with unknown causal graphs for two settings, namely structural causal models with hard interventions and function networks with soft interventions. We propose Graph Agnostic Causal Bayesian Optimisation (GACBO), an algorithm that actively discovers the causal structure that contributes to achieving optimal rewards. GACBO seeks to balance exploiting the actions that give the best rewards against exploring the causal structures and functions. To the best of our knowledge, our work is the first to study causal Bayesian optimization with cumulative regret objectives in scenarios where the graph is unknown or partially known. We show our proposed algorithm outperforms baselines in simulated experiments and real-world applications.

Two-Stage Neural Contextual Bandits for Personalised News Recommendation

We consider the problem of personalised news recommendation where each user consumes news in a sequential fashion. Existing personalised news recommendation methods focus on exploiting user interests and ignores exploration in recommendation, which leads to biased feedback loops and hurt recommendation quality in the long term. We build on contextual bandits recommendation strategies which naturally address the exploitation-exploration trade-off. The main challenges are the computational efficiency for exploring the large-scale item space and utilising the deep representations with uncertainty. We propose a two-stage hierarchical topic-news deep contextual bandits framework to efficiently learn user preferences when there are many news items. We use deep learning representations for users and news, and generalise the neural upper confidence bound (UCB) policies to generalised additive UCB and bilinear UCB. Empirical results on a large-scale news recommendation dataset show that our proposed policies are efficient and outperform the baseline bandit policies.

Gaussian Process Bandits with Aggregated Feedback

We consider the continuum-armed bandits problem, under a novel setting of recommending the best arms within a fixed budget under aggregated feedback. This is motivated by applications where the precise rewards are impossible or expensive to obtain, while an aggregated reward or feedback, such as the average over a subset, is available. We constrain the set of reward functions by assuming that they are from a Gaussian Process and propose the Gaussian Process Optimistic Optimisation (GPOO) algorithm. We adaptively construct a tree with nodes as subsets of the arm space, where the feedback is the aggregated reward of representatives of a node. We propose a new simple regret notion with respect to aggregated feedback on the recommended arms. We provide theoretical analysis for the proposed algorithm, and recover single point feedback as a special case. We illustrate GPOO and compare it with related algorithms on simulated data.

Quantile Bandits for Best Arms Identification with Concentration Inequalities

We consider a variant of the best arm identification task in stochastic multi-armed bandits. Motivated by risk-averse decision-making problems in fields like medicine, biology and finance, our goal is to identify a set of $m$ arms with the highest $\tau$-quantile values under a fixed budget. We propose Quantile Successive Accepts and Rejects algorithm (Q-SAR), the first quantile based algorithm for fixed budget multiple arms identification. We prove two-sided asymmetric concentration inequalities for order statistics and quantiles of random variables that have non-decreasing hazard rate, which may be of independent interest. With the proposed concentration inequalities, we upper bound the probability of arm misidentification for the bandit task. We show illustrative experiments for best arm identification.