Graphon Mixtures

Social networks have a small number of large hubs, and a large number of small dense communities. We propose a generative model that captures both hub and dense structures. Based on recent results about graphons on line graphs, our model is a graphon mixture, enabling us to generate sequences of graphs where each graph is a combination of sparse and dense graphs. We propose a new condition on sparse graphs (the max-degree), which enables us to identify hubs. We show theoretically that we can estimate the normalized degree of the hubs, as well as estimate the graphon corresponding to sparse components of graph mixtures. We illustrate our approach on synthetic data, citation graphs, and social networks, showing the benefits of explicitly modeling sparse graphs.

Position: We need responsible, application-driven (RAD) AI research

This position paper argues that achieving meaningful scientific and societal advances with artificial intelligence (AI) requires a responsible, application-driven approach (RAD) to AI research. As AI is increasingly integrated into society, AI researchers must engage with the specific contexts where AI is being applied. This includes being responsive to ethical and legal considerations, technical and societal constraints, and public discourse. We present the case for RAD-AI to drive research through a three-staged approach: (1) building transdisciplinary teams and people-centred studies; (2) addressing context-specific methods, ethical commitments, assumptions, and metrics; and (3) testing and sustaining efficacy through staged testbeds and a community of practice. We present a vision for the future of application-driven AI research to unlock new value through technically feasible methods that are adaptive to the contextual needs and values of the communities they ultimately serve.

Squared families: Searching beyond regular probability models

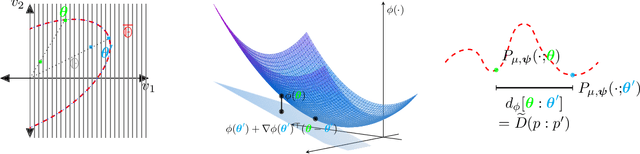
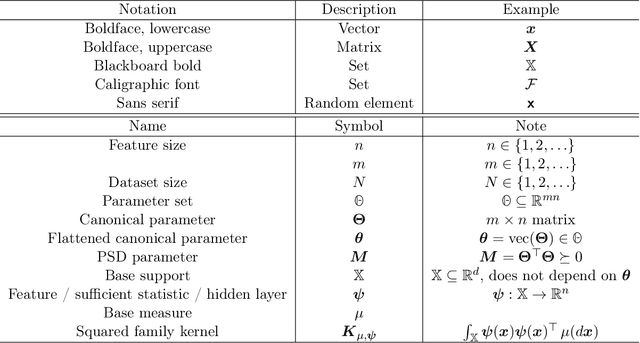
We introduce squared families, which are families of probability densities obtained by squaring a linear transformation of a statistic. Squared families are singular, however their singularity can easily be handled so that they form regular models. After handling the singularity, squared families possess many convenient properties. Their Fisher information is a conformal transformation of the Hessian metric induced from a Bregman generator. The Bregman generator is the normalising constant, and yields a statistical divergence on the family. The normalising constant admits a helpful parameter-integral factorisation, meaning that only one parameter-independent integral needs to be computed for all normalising constants in the family, unlike in exponential families. Finally, the squared family kernel is the only integral that needs to be computed for the Fisher information, statistical divergence and normalising constant. We then describe how squared families are special in the broader class of $g$-families, which are obtained by applying a sufficiently regular function $g$ to a linear transformation of a statistic. After removing special singularities, positively homogeneous families and exponential families are the only $g$-families for which the Fisher information is a conformal transformation of the Hessian metric, where the generator depends on the parameter only through the normalising constant. Even-order monomial families also admit parameter-integral factorisations, unlike exponential families. We study parameter estimation and density estimation in squared families, in the well-specified and misspecified settings. We use a universal approximation property to show that squared families can learn sufficiently well-behaved target densities at a rate of $\mathcal{O}(N^{-1/2})+C n^{-1/4}$, where $N$ is the number of datapoints, $n$ is the number of parameters, and $C$ is some constant.

Generalization Certificates for Adversarially Robust Bayesian Linear Regression

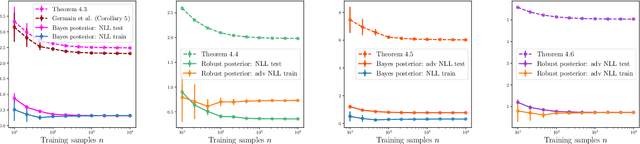
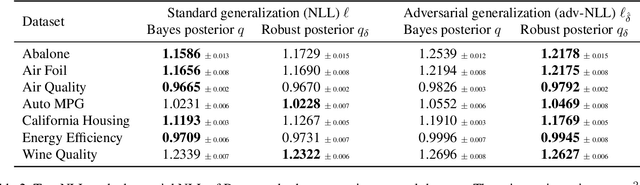
Adversarial robustness of machine learning models is critical to ensuring reliable performance under data perturbations. Recent progress has been on point estimators, and this paper considers distributional predictors. First, using the link between exponential families and Bregman divergences, we formulate an adversarial Bregman divergence loss as an adversarial negative log-likelihood. Using the geometric properties of Bregman divergences, we compute the adversarial perturbation for such models in closed-form. Second, under such losses, we introduce \emph{adversarially robust posteriors}, by exploiting the optimization-centric view of generalized Bayesian inference. Third, we derive the \emph{first} rigorous generalization certificates in the context of an adversarial extension of Bayesian linear regression by leveraging the PAC-Bayesian framework. Finally, experiments on real and synthetic datasets demonstrate the superior robustness of the derived adversarially robust posterior over Bayes posterior, and also validate our theoretical guarantees.

Indirect Query Bayesian Optimization with Integrated Feedback

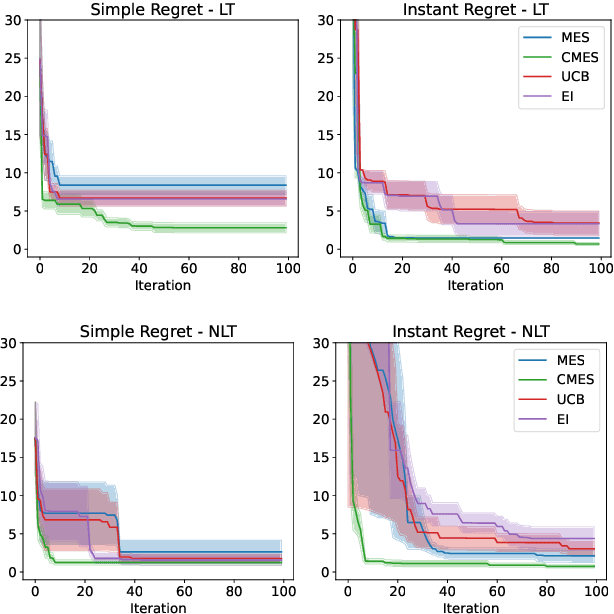
We develop the framework of Indirect Query Bayesian Optimization (IQBO), a new class of Bayesian optimization problems where the integrated feedback is given via a conditional expectation of the unknown function $f$ to be optimized. The underlying conditional distribution can be unknown and learned from data. The goal is to find the global optimum of $f$ by adaptively querying and observing in the space transformed by the conditional distribution. This is motivated by real-world applications where one cannot access direct feedback due to privacy, hardware or computational constraints. We propose the Conditional Max-Value Entropy Search (CMES) acquisition function to address this novel setting, and propose a hierarchical search algorithm to address the multi-resolution setting and improve the computational efficiency. We show regret bounds for our proposed methods and demonstrate the effectiveness of our approaches on simulated optimization tasks.

Variational Search Distributions

We develop variational search distributions (VSD), a method for finding discrete, combinatorial designs of a rare desired class in a batch sequential manner with a fixed experimental budget. We formalize the requirements and desiderata for this problem and formulate a solution via variational inference that fulfill these. In particular, VSD uses off-the-shelf gradient based optimization routines, and can take advantage of scalable predictive models. We show that VSD can outperform existing baseline methods on a set of real sequence-design problems in various biological systems.

Graphons of Line Graphs

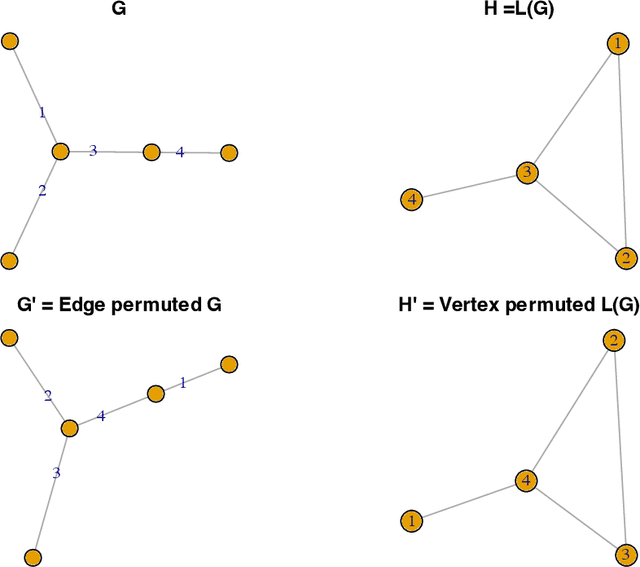
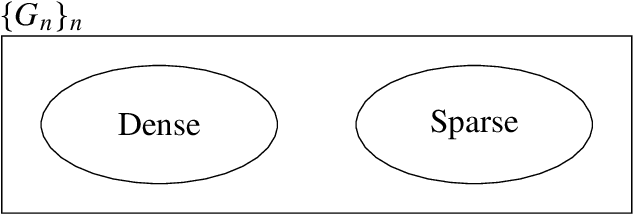
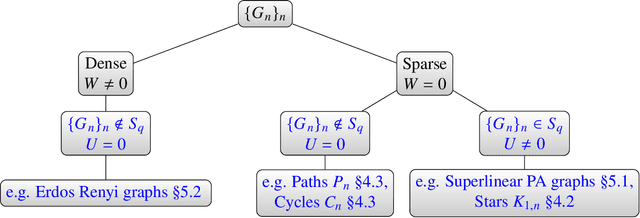
A graphon is the limit of a converging graph sequence. Graphons of dense graphs are useful as they can act as a blueprint and generate graphs of arbitrary size with similar properties. But for sparse graphs this is not the case. Sparse graphs converge to the zero graphon, making the generated graphs empty or edgeless. Thus, the classical graphon definition fails for sparse graphs. Several methods have been proposed to overcome this limitation and to understand sparse graphs more deeply. However, the fragile nature of sparse graphs makes these methods mathematically complex. In this paper we show a simple method that can shed light on a certain subset of sparse graphs. The method involves mapping the original graphs to their line graphs. Line graphs map edges to vertices and connects edges when edges in the original graph share a vertex. We show that graphs satisfying a particular property, which we call the square-degree property are sparse, but give rise to dense line graphs. In particular, star graphs satisfy the square-degree property resulting in dense line graphs and non-zero graphons of line graphs. Similarly, superlinear preferential attachment graphs give rise to dense line graphs almost surely. In contrast, dense graphs, including Erdos-Renyi graphs make the line graphs sparse, resulting in the zero graphon.

Exact, Fast and Expressive Poisson Point Processes via Squared Neural Families

We introduce squared neural Poisson point processes (SNEPPPs) by parameterising the intensity function by the squared norm of a two layer neural network. When the hidden layer is fixed and the second layer has a single neuron, our approach resembles previous uses of squared Gaussian process or kernel methods, but allowing the hidden layer to be learnt allows for additional flexibility. In many cases of interest, the integrated intensity function admits a closed form and can be computed in quadratic time in the number of hidden neurons. We enumerate a far more extensive number of such cases than has previously been discussed. Our approach is more memory and time efficient than naive implementations of squared or exponentiated kernel methods or Gaussian processes. Maximum likelihood and maximum a posteriori estimates in a reparameterisation of the final layer of the intensity function can be obtained by solving a (strongly) convex optimisation problem using projected gradient descent. We demonstrate SNEPPPs on real, and synthetic benchmarks, and provide a software implementation. https://github.com/RussellTsuchida/snefy

Uncertainty Quantification of the Virial Black Hole Mass with Conformal Prediction

Precise measurements of the black hole mass are essential to gain insight on the black hole and host galaxy co-evolution. A direct measure of the black hole mass is often restricted to nearest galaxies and instead, an indirect method using the single-epoch virial black hole mass estimation is used for objects at high redshifts. However, this method is subjected to biases and uncertainties as it is reliant on the scaling relation from a small sample of local active galactic nuclei. In this study, we propose the application of conformalised quantile regression (CQR) to quantify the uncertainties of the black hole predictions in a machine learning setting. We compare CQR with various prediction interval techniques and demonstrated that CQR can provide a more useful prediction interval indicator. In contrast to baseline approaches for prediction interval estimation, we show that the CQR method provides prediction intervals that adjust to the black hole mass and its related properties. That is it yields a tighter constraint on the prediction interval (hence more certain) for a larger black hole mass, and accordingly, bright and broad spectral line width source. Using a combination of neural network model and CQR framework, the recovered virial black hole mass predictions and uncertainties are comparable to those measured from the Sloan Digital Sky Survey. The code is publicly available at https://github.com/yongsukyee/uncertain_blackholemass.

Squared Neural Families: A New Class of Tractable Density Models

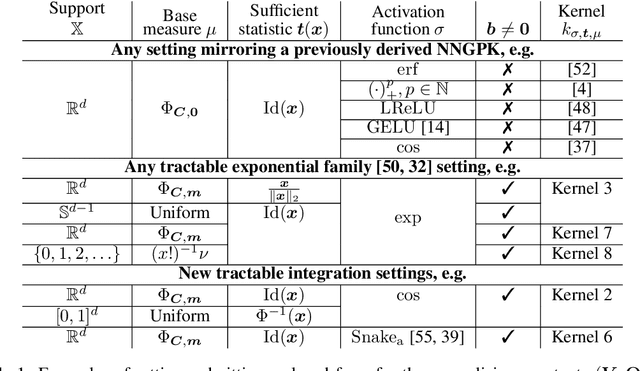
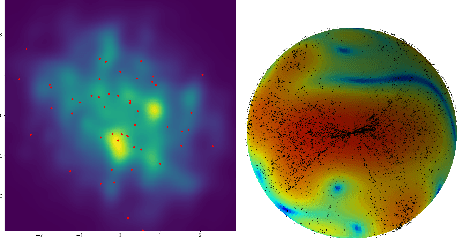
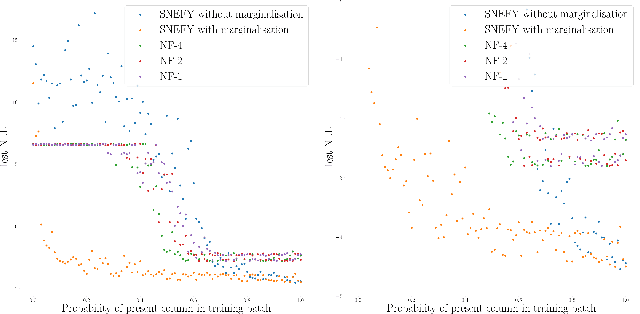
Flexible models for probability distributions are an essential ingredient in many machine learning tasks. We develop and investigate a new class of probability distributions, which we call a Squared Neural Family (SNEFY), formed by squaring the 2-norm of a neural network and normalising it with respect to a base measure. Following the reasoning similar to the well established connections between infinitely wide neural networks and Gaussian processes, we show that SNEFYs admit a closed form normalising constants in many cases of interest, thereby resulting in flexible yet fully tractable density models. SNEFYs strictly generalise classical exponential families, are closed under conditioning, and have tractable marginal distributions. Their utility is illustrated on a variety of density estimation and conditional density estimation tasks. Software available at https://github.com/RussellTsuchida/snefy.