Mahalakshmi Sabanayagam
Robustness Certificates for Neural Networks against Adversarial Attacks
Dec 24, 2025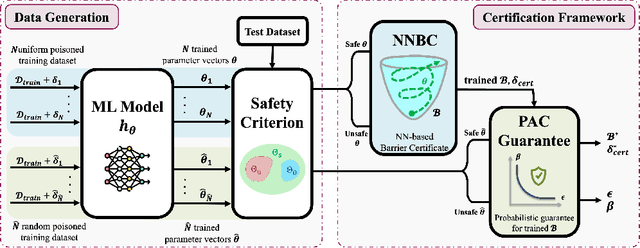
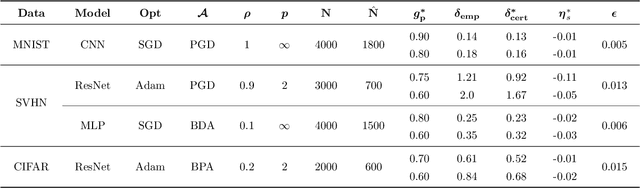
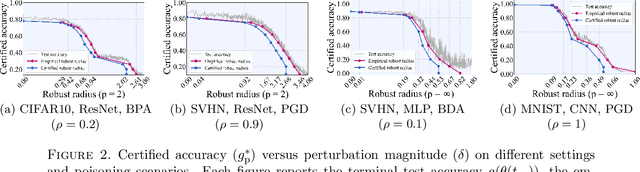
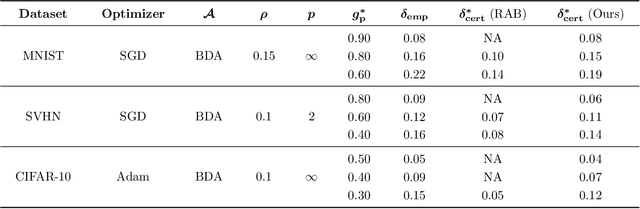
Abstract:The increasing use of machine learning in safety-critical domains amplifies the risk of adversarial threats, especially data poisoning attacks that corrupt training data to degrade performance or induce unsafe behavior. Most existing defenses lack formal guarantees or rely on restrictive assumptions about the model class, attack type, extent of poisoning, or point-wise certification, limiting their practical reliability. This paper introduces a principled formal robustness certification framework that models gradient-based training as a discrete-time dynamical system (dt-DS) and formulates poisoning robustness as a formal safety verification problem. By adapting the concept of barrier certificates (BCs) from control theory, we introduce sufficient conditions to certify a robust radius ensuring that the terminal model remains safe under worst-case ${\ell}_p$-norm based poisoning. To make this practical, we parameterize BCs as neural networks trained on finite sets of poisoned trajectories. We further derive probably approximately correct (PAC) bounds by solving a scenario convex program (SCP), which yields a confidence lower bound on the certified robustness radius generalizing beyond the training set. Importantly, our framework also extends to certification against test-time attacks, making it the first unified framework to provide formal guarantees in both training and test-time attack settings. Experiments on MNIST, SVHN, and CIFAR-10 show that our approach certifies non-trivial perturbation budgets while being model-agnostic and requiring no prior knowledge of the attack or contamination level.
Generalization Certificates for Adversarially Robust Bayesian Linear Regression
Feb 20, 2025
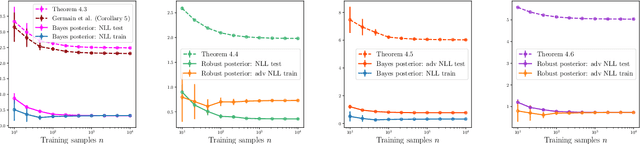
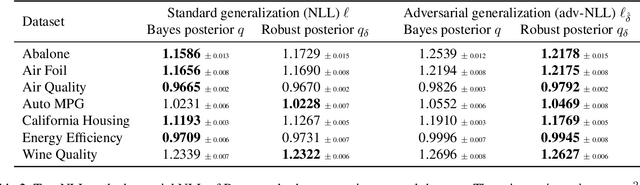
Abstract:Adversarial robustness of machine learning models is critical to ensuring reliable performance under data perturbations. Recent progress has been on point estimators, and this paper considers distributional predictors. First, using the link between exponential families and Bregman divergences, we formulate an adversarial Bregman divergence loss as an adversarial negative log-likelihood. Using the geometric properties of Bregman divergences, we compute the adversarial perturbation for such models in closed-form. Second, under such losses, we introduce \emph{adversarially robust posteriors}, by exploiting the optimization-centric view of generalized Bayesian inference. Third, we derive the \emph{first} rigorous generalization certificates in the context of an adversarial extension of Bayesian linear regression by leveraging the PAC-Bayesian framework. Finally, experiments on real and synthetic datasets demonstrate the superior robustness of the derived adversarially robust posterior over Bayes posterior, and also validate our theoretical guarantees.
Cluster Specific Representation Learning
Dec 04, 2024Abstract:Representation learning aims to extract meaningful lower-dimensional embeddings from data, known as representations. Despite its widespread application, there is no established definition of a ``good'' representation. Typically, the representation quality is evaluated based on its performance in downstream tasks such as clustering, de-noising, etc. However, this task-specific approach has a limitation where a representation that performs well for one task may not necessarily be effective for another. This highlights the need for a more agnostic formulation, which is the focus of our work. We propose a downstream-agnostic formulation: when inherent clusters exist in the data, the representations should be specific to each cluster. Under this idea, we develop a meta-algorithm that jointly learns cluster-specific representations and cluster assignments. As our approach is easy to integrate with any representation learning framework, we demonstrate its effectiveness in various setups, including Autoencoders, Variational Autoencoders, Contrastive learning models, and Restricted Boltzmann Machines. We qualitatively compare our cluster-specific embeddings to standard embeddings and downstream tasks such as de-noising and clustering. While our method slightly increases runtime and parameters compared to the standard model, the experiments clearly show that it extracts the inherent cluster structures in the data, resulting in improved performance in relevant applications.
Exact Certification of (Graph) Neural Networks Against Label Poisoning
Nov 30, 2024



Abstract:Machine learning models are highly vulnerable to label flipping, i.e., the adversarial modification (poisoning) of training labels to compromise performance. Thus, deriving robustness certificates is important to guarantee that test predictions remain unaffected and to understand worst-case robustness behavior. However, for Graph Neural Networks (GNNs), the problem of certifying label flipping has so far been unsolved. We change this by introducing an exact certification method, deriving both sample-wise and collective certificates. Our method leverages the Neural Tangent Kernel (NTK) to capture the training dynamics of wide networks enabling us to reformulate the bilevel optimization problem representing label flipping into a Mixed-Integer Linear Program (MILP). We apply our method to certify a broad range of GNN architectures in node classification tasks. Thereby, concerning the worst-case robustness to label flipping: $(i)$ we establish hierarchies of GNNs on different benchmark graphs; $(ii)$ quantify the effect of architectural choices such as activations, depth and skip-connections; and surprisingly, $(iii)$ uncover a novel phenomenon of the robustness plateauing for intermediate perturbation budgets across all investigated datasets and architectures. While we focus on GNNs, our certificates are applicable to sufficiently wide NNs in general through their NTK. Thus, our work presents the first exact certificate to a poisoning attack ever derived for neural networks, which could be of independent interest.
Provable Robustness of (Graph) Neural Networks Against Data Poisoning and Backdoor Attacks
Jul 15, 2024
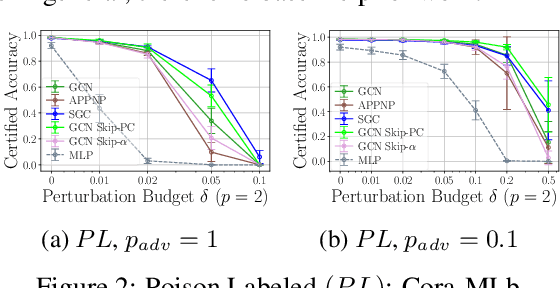
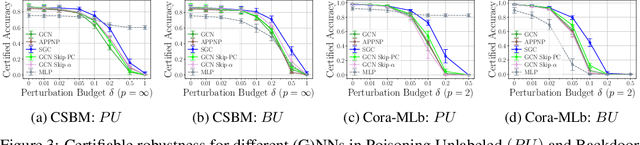
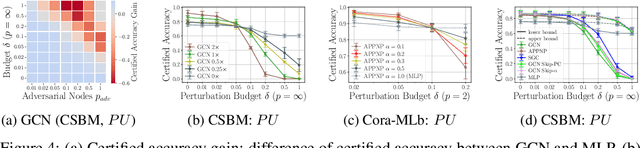
Abstract:Generalization of machine learning models can be severely compromised by data poisoning, where adversarial changes are applied to the training data, as well as backdoor attacks that additionally manipulate the test data. These vulnerabilities have led to interest in certifying (i.e., proving) that such changes up to a certain magnitude do not affect test predictions. We, for the first time, certify Graph Neural Networks (GNNs) against poisoning and backdoor attacks targeting the node features of a given graph. Our certificates are white-box and based upon $(i)$ the neural tangent kernel, which characterizes the training dynamics of sufficiently wide networks; and $(ii)$ a novel reformulation of the bilevel optimization problem describing poisoning as a mixed-integer linear program. Consequently, we leverage our framework to provide fundamental insights into the role of graph structure and its connectivity on the worst-case robustness behavior of convolution-based and PageRank-based GNNs. We note that our framework is more general and constitutes the first approach to derive white-box poisoning certificates for NNs, which can be of independent interest beyond graph-related tasks.
Fast Adaptive Test-Time Defense with Robust Features
Jul 21, 2023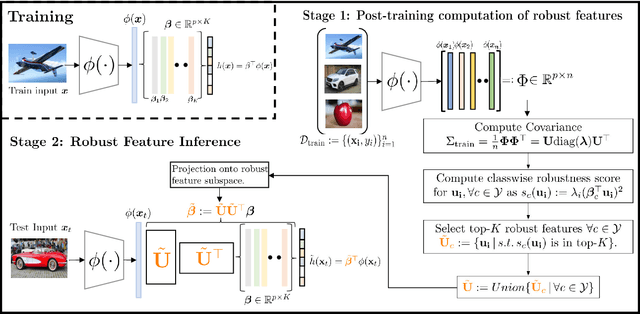

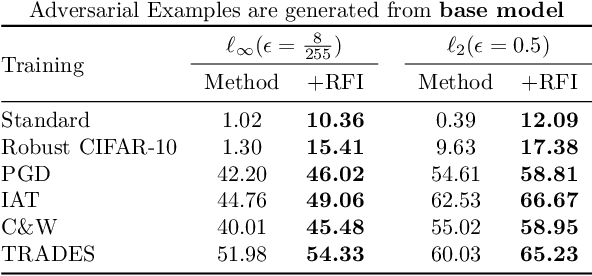
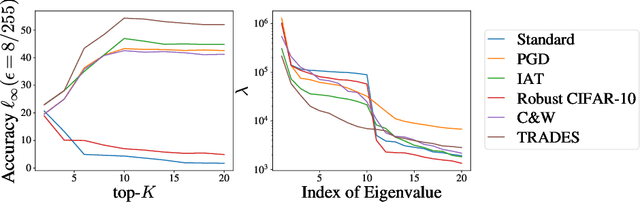
Abstract:Adaptive test-time defenses are used to improve the robustness of deep neural networks to adversarial examples. However, existing methods significantly increase the inference time due to additional optimization on the model parameters or the input at test time. In this work, we propose a novel adaptive test-time defense strategy that is easy to integrate with any existing (robust) training procedure without additional test-time computation. Based on the notion of robustness of features that we present, the key idea is to project the trained models to the most robust feature space, thereby reducing the vulnerability to adversarial attacks in non-robust directions. We theoretically show that the top eigenspace of the feature matrix are more robust for a generalized additive model and support our argument for a large width neural network with the Neural Tangent Kernel (NTK) equivalence. We conduct extensive experiments on CIFAR-10 and CIFAR-100 datasets for several robustness benchmarks, including the state-of-the-art methods in RobustBench, and observe that the proposed method outperforms existing adaptive test-time defenses at much lower computation costs.
Kernels, Data & Physics
Jul 05, 2023Abstract:Lecture notes from the course given by Professor Julia Kempe at the summer school "Statistical physics of Machine Learning" in Les Houches. The notes discuss the so-called NTK approach to problems in machine learning, which consists of gaining an understanding of generally unsolvable problems by finding a tractable kernel formulation. The notes are mainly focused on practical applications such as data distillation and adversarial robustness, examples of inductive bias are also discussed.
Unveiling the Hessian's Connection to the Decision Boundary
Jun 12, 2023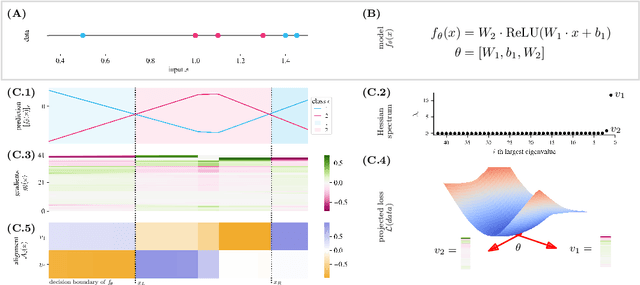



Abstract:Understanding the properties of well-generalizing minima is at the heart of deep learning research. On the one hand, the generalization of neural networks has been connected to the decision boundary complexity, which is hard to study in the high-dimensional input space. Conversely, the flatness of a minimum has become a controversial proxy for generalization. In this work, we provide the missing link between the two approaches and show that the Hessian top eigenvectors characterize the decision boundary learned by the neural network. Notably, the number of outliers in the Hessian spectrum is proportional to the complexity of the decision boundary. Based on this finding, we provide a new and straightforward approach to studying the complexity of a high-dimensional decision boundary; show that this connection naturally inspires a new generalization measure; and finally, we develop a novel margin estimation technique which, in combination with the generalization measure, precisely identifies minima with simple wide-margin boundaries. Overall, this analysis establishes the connection between the Hessian and the decision boundary and provides a new method to identify minima with simple wide-margin decision boundaries.
Improved Representation Learning Through Tensorized Autoencoders
Dec 02, 2022
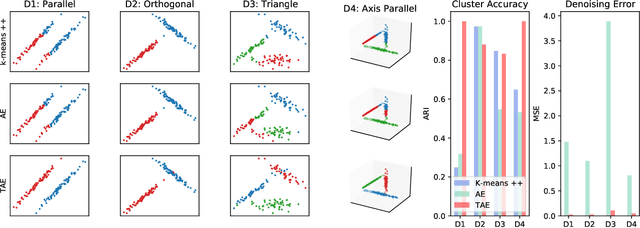
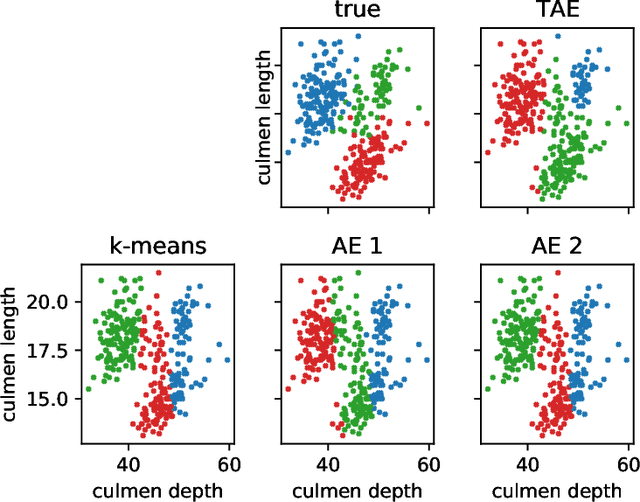
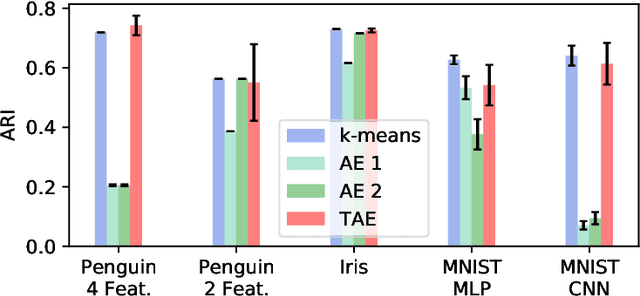
Abstract:The central question in representation learning is what constitutes a good or meaningful representation. In this work we argue that if we consider data with inherent cluster structures, where clusters can be characterized through different means and covariances, those data structures should be represented in the embedding as well. While Autoencoders (AE) are widely used in practice for unsupervised representation learning, they do not fulfil the above condition on the embedding as they obtain a single representation of the data. To overcome this we propose a meta-algorithm that can be used to extend an arbitrary AE architecture to a tensorized version (TAE) that allows for learning cluster-specific embeddings while simultaneously learning the cluster assignment. For the linear setting we prove that TAE can recover the principle components of the different clusters in contrast to principle component of the entire data recovered by a standard AE. We validated this on planted models and for general, non-linear and convolutional AEs we empirically illustrate that tensorizing the AE is beneficial in clustering and de-noising tasks.
Representation Power of Graph Convolutions : Neural Tangent Kernel Analysis
Oct 18, 2022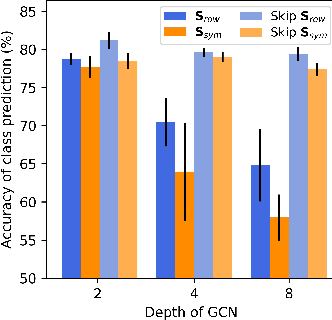
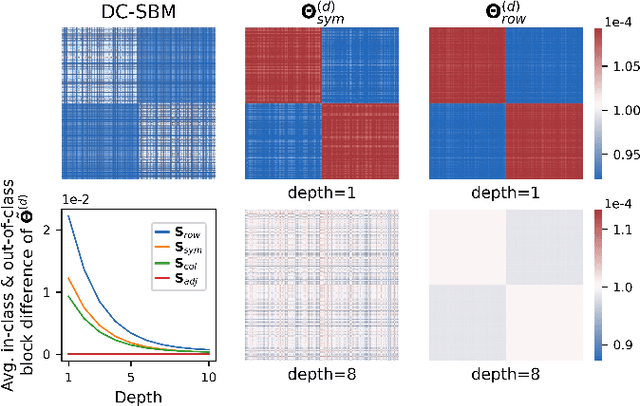
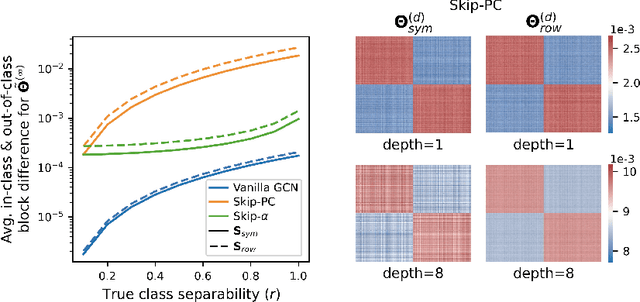
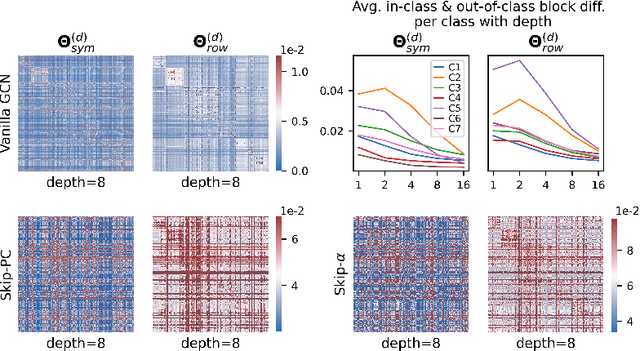
Abstract:The fundamental principle of Graph Neural Networks (GNNs) is to exploit the structural information of the data by aggregating the neighboring nodes using a graph convolution. Therefore, understanding its influence on the network performance is crucial. Convolutions based on graph Laplacian have emerged as the dominant choice with the symmetric normalization of the adjacency matrix $A$, defined as $D^{-1/2}AD^{-1/2}$, being the most widely adopted one, where $D$ is the degree matrix. However, some empirical studies show that row normalization $D^{-1}A$ outperforms it in node classification. Despite the widespread use of GNNs, there is no rigorous theoretical study on the representation power of these convolution operators, that could explain this behavior. In this work, we analyze the influence of the graph convolutions theoretically using Graph Neural Tangent Kernel in a semi-supervised node classification setting. Under a Degree Corrected Stochastic Block Model, we prove that: (i) row normalization preserves the underlying class structure better than other convolutions; (ii) performance degrades with network depth due to over-smoothing, but the loss in class information is the slowest in row normalization; (iii) skip connections retain the class information even at infinite depth, thereby eliminating over-smoothing. We finally validate our theoretical findings on real datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge