Deconstructing the Goldilocks Zone of Neural Network Initialization

The second-order properties of the training loss have a massive impact on the optimization dynamics of deep learning models. Fort & Scherlis (2019) discovered that a high positive curvature and local convexity of the loss Hessian are associated with highly trainable initial points located in a region coined the "Goldilocks zone". Only a handful of subsequent studies touched upon this relationship, so it remains largely unexplained. In this paper, we present a rigorous and comprehensive analysis of the Goldilocks zone for homogeneous neural networks. In particular, we derive the fundamental condition resulting in non-zero positive curvature of the loss Hessian and argue that it is only incidentally related to the initialization norm, contrary to prior beliefs. Further, we relate high positive curvature to model confidence, low initial loss, and a previously unknown type of vanishing cross-entropy loss gradient. To understand the importance of positive curvature for trainability of deep networks, we optimize both fully-connected and convolutional architectures outside the Goldilocks zone and analyze the emergent behaviors. We find that strong model performance is not necessarily aligned with the Goldilocks zone, which questions the practical significance of this concept.

Unveiling the Hessian's Connection to the Decision Boundary

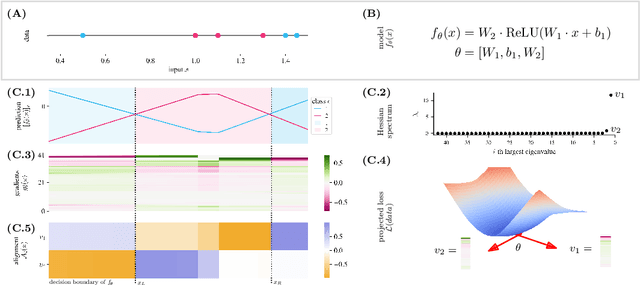
Understanding the properties of well-generalizing minima is at the heart of deep learning research. On the one hand, the generalization of neural networks has been connected to the decision boundary complexity, which is hard to study in the high-dimensional input space. Conversely, the flatness of a minimum has become a controversial proxy for generalization. In this work, we provide the missing link between the two approaches and show that the Hessian top eigenvectors characterize the decision boundary learned by the neural network. Notably, the number of outliers in the Hessian spectrum is proportional to the complexity of the decision boundary. Based on this finding, we provide a new and straightforward approach to studying the complexity of a high-dimensional decision boundary; show that this connection naturally inspires a new generalization measure; and finally, we develop a novel margin estimation technique which, in combination with the generalization measure, precisely identifies minima with simple wide-margin boundaries. Overall, this analysis establishes the connection between the Hessian and the decision boundary and provides a new method to identify minima with simple wide-margin decision boundaries.

Introduction to Latent Variable Energy-Based Models: A Path Towards Autonomous Machine Intelligence

Current automated systems have crucial limitations that need to be addressed before artificial intelligence can reach human-like levels and bring new technological revolutions. Among others, our societies still lack Level 5 self-driving cars, domestic robots, and virtual assistants that learn reliable world models, reason, and plan complex action sequences. In these notes, we summarize the main ideas behind the architecture of autonomous intelligence of the future proposed by Yann LeCun. In particular, we introduce energy-based and latent variable models and combine their advantages in the building block of LeCun's proposal, that is, in the hierarchical joint embedding predictive architecture (H-JEPA).